Published online by Cambridge University Press: 22 January 2016
Let 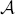 be a simple Abelian variety of dimension g over ℚ, and let ℓ be the rank of the Mordell-Weil group
be a simple Abelian variety of dimension g over ℚ, and let ℓ be the rank of the Mordell-Weil group 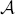 (ℚ). Assume ℓ ≥ 1. A conjecture of Mazur asserts that the closure of
(ℚ). Assume ℓ ≥ 1. A conjecture of Mazur asserts that the closure of 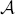 (ℚ) into
(ℚ) into 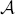 (ℝ) for the real topology contains the neutral component
(ℝ) for the real topology contains the neutral component 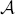 (ℝ)0 of the origin. This is known only under the extra hypothesis ℓ ≥ g2 - g + 1. We investigate here a quantitative refinement of this question: for each given positive h, the set of points in
(ℝ)0 of the origin. This is known only under the extra hypothesis ℓ ≥ g2 - g + 1. We investigate here a quantitative refinement of this question: for each given positive h, the set of points in 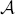 (ℚ) of Néron-Tate height ≤ h is finite, and we study how these points are distributed into the connected component
(ℚ) of Néron-Tate height ≤ h is finite, and we study how these points are distributed into the connected component 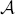 (ℝ)0. More generally we consider an Abelian variety A over a number field K embedded in ℝ, and a subgroup Γ of
(ℝ)0. More generally we consider an Abelian variety A over a number field K embedded in ℝ, and a subgroup Γ of 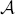 (K) of sufficiently large rank. The effective result of density we obtain relies on an estimate of Diophantine approximation, namely a lower bound for linear combinations of determinants involving Abelian logarithms.
(K) of sufficiently large rank. The effective result of density we obtain relies on an estimate of Diophantine approximation, namely a lower bound for linear combinations of determinants involving Abelian logarithms.