Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:07:56.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Définition des pseudogroupes infinitésimaux de Lie intransitifs—Théorème fondamental de réalisation en dimension deux

Published online by Cambridge University Press:  22 January 2016

Ngô van Quê  and
Vo van Tho
Ngô van Quê
Affiliation:
Université de Montréal
Vo van Tho
Affiliation:
Université de Montréal
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit G un groupe de Lie opérant de manière localement effective sur une variété différentiable M. Pour tout sous-groupe à un paramètre {gt, t ∈ R} de G, on a le champ de vecteurs associé X dit de Killing sur M:

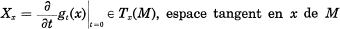
Le faisceau correspondant de tous les champs de vecteurs de Killing du groupe de transformations G sera noté par θ; il est démontré [7] qu’il existe un ouvert ^ partout dense dans M, dit de régularité tel que:

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 86 , June 1982 , pp. 211 - 228
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1982

References

Références

[ 1 ] Van Quê, Ngô et Tho, Vo Van, Classification des groupes locaux transformations holomorphes sur C , Rapport de Recherches du Département de Mathématiques et Statistique No. 79–8, Université de Montréal, à paraitre.Google Scholar
[ 2 ] Cartan, Elie, Les sous-groupes des groupes continus de transformations, Oeuvres complètes, Partie II, 2 (1953), 719–856.Google Scholar
[ 3 ] Rodrigues, A. A. M. et Van Quê, Ngô, Troisième théorème fondamental de réalisation de Cartan, Annales de l’institut de Fourier, XXV, fasc. 1 (1975), 251–282.Google Scholar