Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-25T21:30:33.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of representations of SL(2, C) induced by the continuous series of E(2)

Published online by Cambridge University Press:  22 January 2016

Hitoshi Kaneta
Hitoshi Kaneta*
Affiliation:
Department of MathematicsNagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Since the representations of SL(2, C) induced by irreducible unitary representations of 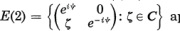appear as the restriction to the Lorentz group of some irreducible unitary representations of the inhomogeneous Lorentz group, the decomposition of the induced representations deserves our investigation. For the representations of SL(2, C) induced by irreducible unitary representations with discrete spin of E(2), the decomposition has been obtained by Mukunda [9]. We hope that our analysis will justify the calculations by Chakrabarti [1], [2] and [3].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 78 , May 1980 , pp. 95 - 111
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

[1] Chakrabarti, A., Lévy-Nahas, M. and Seveor, R., Lorentz basis of the Poincaré group, J. Math. Phys. 9 (1968), 1274–1283.CrossRefGoogle Scholar
[2] Chakrabarti, A., Remarks on lighlike continuous spin and spacelike representations of the Poincaré group, J. Math. Phys. 12 (1971), 1813–1822.CrossRefGoogle Scholar
[3] Chakrabarti, A., Lorentz basis of the Poincaré group, II, J. Math. Phys. 12 (1971), 1822–1840.Google Scholar
[4] Coddington, E. A. and Levinson, N., Theory of ordinary differential equations McGraw-Hill, 1955.Google Scholar
[5] Itatsu, S. and Kaneta, H., Spectral properties of first order ordinary differential operators, to appear.Google Scholar
[6] Kaneta, H., Irreducibility of some unitary representations of the Poincaré group with respect to the Poincaré subsemigroup, Nagoya Math. J., 78 (1980), 113–136.CrossRefGoogle Scholar
[7] Kato, T., Perturbation theory for linear operators, Springer, 1966.Google Scholar
[8] Moriguchi, S. et al., Sugaku koshiki III, Iwanami (in Japanese).Google Scholar
[9] Mukunda, N., Zero-mass representations of the Poincaré group in an 0(3, 1) basis, J. Math. Phys. 9 (1968), 532–536.CrossRefGoogle Scholar
[10] Naimark, M. A., Linear representation of Lorentz group, VEB Deucher Verlag der Wissenschaften Berlin, 1963.Google Scholar
[11] Radhakrishnan, B. and Mukunda, N., Spacelike representations of the inhomogeneous Lorentz basis, J. Math. Phys. 15 (1974), 477–490.Google Scholar
[12] Yoshida, K., Functional analysis, Springer, 1965.Google Scholar