Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Louboutin, Stéphane
1990.
Les extensions quadratiques du corps des rationnels, ou du corps de Causs, ou du corps des racines cubiques de l'unité de calibres 1.
Manuscripta Mathematica,
Vol. 69,
Issue. 1,
p.
387.
Hashimoto, Ryūta
1999.
Explicit representations of classes of some binary quadratic forms of discriminants $4q^2+1$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 75,
Issue. 1,


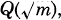 ,
, 