Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fomenko, O. M.
1992.
Distribution of the roots of a quadratic congruence.
Journal of Soviet Mathematics,
Vol. 62,
Issue. 4,
p.
2936.
Fomenko, O. M.
1998.
Distribution of values of Fourier coefficients for modular forms of weight 1.
Journal of Mathematical Sciences,
Vol. 89,
Issue. 1,
p.
1050.
Fomenko, O. M.
1999.
Fourier coefficients of cusp forms and automorphic f-functions.
Journal of Mathematical Sciences,
Vol. 95,
Issue. 3,
p.
2295.
Voskresenskaya, G. V.
2012.
Arithmetic properties of shimura sums related to several modular forms.
Journal of Mathematical Sciences,
Vol. 182,
Issue. 4,
p.
444.
Fomenko, O. M.
2014.
On the Dedekind Zeta Function.
Journal of Mathematical Sciences,
Vol. 200,
Issue. 5,
p.
624.
Voskresenskaya, G. V.
2014.
The Dedekind Eta-Function in Algebra and Number Theory: Old and New Problems.
Journal of Mathematical Sciences,
Vol. 199,
Issue. 3,
p.
248.
Fomenko, O. M.
2015.
On the Dedekind Zeta Function. II.
Journal of Mathematical Sciences,
Vol. 207,
Issue. 6,
p.
923.
Fomenko, O. M.
2016.
On the Mean Square of the Error Term For Dedekind Zeta Functions.
Journal of Mathematical Sciences,
Vol. 217,
Issue. 1,
p.
125.
Voskresenskaya, G. V.
2018.
Dedekind η-Function in Modern Research.
Journal of Mathematical Sciences,
Vol. 235,
Issue. 6,
p.
788.


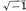 and
and 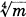 . Then its Galois group over
. Then its Galois group over 