Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T15:25:55.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Cusp forms of weight 3/2

Published online by Cambridge University Press:  22 January 2016

Hisashi Kojima
Hisashi Kojima*
Affiliation:
Mathematical Institute, Tohoku University, Sendai, 980Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we deal with the problem (C) in § 4 of [4]. Let Ik be the Shimura mapping in [4] of Sk(4N, χ) into 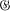k-1(N′ χ2) (see p. 458). The problem (C) can be stated as follows: I3(f) is a cusp form if and only if ‹f, h› = 0 for all h ∈ U, where U is the vector space spanned by every theta series of S3(4N, χ) associated with some Dirichlet character.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 79 , October 1980 , pp. 111 - 122
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

[ 1 ] Doi-Miyake, , Automorphic forms and number theory (Japanese) Kinokuniya Shoten, Tokyo (1976).Google Scholar
[ 2 ] Niwa, S., Modular forms of half integral weight and the integral certain thetafunctions, Nagoya Math. J., 56 (1975), 147–161.Google Scholar
[ 3 ] Serre, J.-P. and Stark, H. M., Modular forms of weight 1/2, Springer Lecture Notes, 627 (1977), 29–66.Google Scholar
[ 4 ] Shimura, G., On modular forms of half integral weight, Ann. of Math., 97 (1973), 440–481.CrossRefGoogle Scholar
[ 5 ] Shimura, G., The special values of the zeta functions associated with cusp forms, Comm. Pure Appl. Math., 29 (1976), 783–804.Google Scholar
[ 6 ] Shintani, T., On construction of holomorphic cusp forms of half integral weight, Nagoya Math. J., 58 (1975), 83–126.Google Scholar