No CrossRef data available.
Article contents
Cores of Potential Operators for Processes With Stationary Independent Increments
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Xt(ω)) be a stochastic process with stationary independent increments on the N-dimensional Euclidean space RN, right continuous in t ≧ 0 and starting at the origin. Let C0(RN) be the Banach space of real-valued continuous functions on RN vanishing at infinity with norm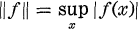 
. The process induces a transition semigroup of operators Tt on C0(RN) :
Ttf(x) = Ef(x + Xt).
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1972
References
[1]
Courrège, P., Générateur infinitésimal d’un semi-groupe de convolution sur Rn
, et formule de Lévy-Khinchine, Bull. Sci. Math., 2
e série, 88 (1964), 3–30.Google Scholar
[2]
Port, S. C. and Stone, C. J., Infinitely divisible processes and their potential theory (First part), Ann. Inst. Fourier (Grenoble), 21, 2 (1971), 157–275; (Second part) 21, 4 (1971), 179–265.Google Scholar
[3]
Sato, K., Semigroups and Markov processes, Lecture notes at University of Minnesota (1968).Google Scholar
[4]
Sato, K., Potential operators for Markov processes, Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, 3, to appear.Google Scholar
[5]
Sato, K., A note on infinitely divisible distributions and their Levy measures, to appear.Google Scholar
[6]
Watanabe, S., A limit theorem of branching processes and continuous state branching processes, J. Math. Kyoto Univ., 8 (1968), 141–167.Google Scholar
[7]
Yosida, K., The existence of the potential operator associated with an equi-continuous semigroup of class (Co), Studia Math. 31 (1968), 531–533.Google Scholar
You have
Access