Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T01:12:34.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of the zeta functions of prehomogeneous vector spaces

Published online by Cambridge University Press:  22 January 2016

Hiroshi Saito
Hiroshi Saito*
Affiliation:
Department of Mathematics, Faculty of Science, Kyoto University, Kyoto 606-8502, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (G, ρ, X) be a prehomogeneous vector space with singular set S over an algebraic number field F. The main result of this paper is a proof for the convergence of the zeta fucntions Z(Φ, s) associated with (G, ρ, X) for large Re s under the assumption that S is a hypersurface. This condition is satisfied if G is reductive and (G, ρ, X) is regular. When the connected component 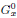of the stabilizer of a generic point x is semisimple and the group Πx of connected components of Gx is abelian, a clear estimate of the domain of convergence is given.

Moreover when S is a hypersurface and the Hasse principle holds for G, it is shown that the zeta fucntions are sums of (usually infinite) Euler products, the local components of which are orbital local zeta functions. This result has been proved in a previous paper by the author under the more restrictive condition that (G, ρ, X) is irreducible, regular, and reduced, and the zeta function is absolutely convergent.

Keywords

11E4511E72
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 170 , 2003 , pp. 1 - 31
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2003

References

[B] Borovoi, M., Abelian Galois cohomology of reductive groups, Mem. of A. M. S., 132 (1998), No. 626, viii+50 pp.CrossRefGoogle Scholar
[Br] Brauer, R., On zeta functions of algebraic number fields I,II, Amer. J. Math., 69 (1947), 243–150, 739–746.CrossRefGoogle Scholar
[B-T] Borel, A. and Tits, J., Groupes algébriques sur un corps local Ch.III, Compléments et applications à la cohomologie galoisienne, J. Fac. Sci. Univ. Tokyo, 34 (1987), 671–698.Google Scholar
[K1] Kottwitz, R. E., Stable trace formula:cuspidal tempered terms, Duke Math. J., 51 (1984), 611–650.CrossRefGoogle Scholar
[K2] Kottwitz, R. E., Stable trace formula:elliptic singular terms, Math. Ann., 275 (1986), 365–399.CrossRefGoogle Scholar
[L] Landau, E., Zur Theorie der Heckeshcen Zetafuktionen, welche komplexen Charakteren entsprechen, Math. Z., 4 (1919), 152–162..CrossRefGoogle Scholar
[L-W] Lang, S. and Weil, A., Number of points of varieties in finite fields, Amer. J. Math., 76 (1954), 819–827.CrossRefGoogle Scholar
[O] Ono, T., An integral attached to a hypersurface, Amer. J. Math., 90 (1968), 1224–1236.CrossRefGoogle Scholar
[P-R] Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Academic Press, 1994.Google Scholar
[Sa1] Saito, H., Explicit form of the zeta functions of prehomogeneous vector spaces, Math. Ann., 315 (1999), 587–615.CrossRefGoogle Scholar
[Sa2] Saito, H., Explicit formula of orbital p-adic zeta fucntions associated to symmetric and hermitian matrices, Comm. Math. Univ. Sancti Pauli, 46 (1997), 175–216.Google Scholar
[S1] Sato, F., Zeta functions in several variables associated with prehomogeneous vector spaces I: Functional equations, Tohoku Math. J., 34 (1982), 437–483.CrossRefGoogle Scholar
[S2] Sato, F., Zeta functions in several variables associated with prehomogeneous vector spaces II: A convergence criterion, Tohoku Math. J., 35 (1983), 77–99.Google Scholar
[S3] Sato, F., Report on the convergence of zeta functions associated with prehomoge neous vector spaces, RIMS kokyuroku, 924 (1995), 61–73.Google Scholar
[S-K] Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector spaces and their relative invariants, Nagoya Math. J., 65 (1977), 1–155.CrossRefGoogle Scholar
[S-S] Sato, M. and Shintani, T., On zeta functions associated with prehomogeneous vec tor spaces, Ann. of Math., 100 (1974), 131–170.CrossRefGoogle Scholar
[Se] Serre, J. P., Cohomologie Galoisienne, Lecture Notes in Math. vol. 8, Springer-Verlag, Berlin, 1964.Google Scholar
[Y] Yin, K., On the convergence of the adelic zeta functions associated to irreducible regular prehomogeneous vector spaces, Amer. Math. J., 117 (1995), 457–490.CrossRefGoogle Scholar
[Yu1] Yukie, A., Shintani zeta fucntions London Math. Soc. Lecture Notes Series 183, Cambridge Univ. Press, 1993.CrossRefGoogle Scholar
[Yu2] Yukie, A., On the convergence of the zeta fucntions for certain prehomogeneous vector spaces, Nagoya Math. J., 140 (1995), 1–31.CrossRefGoogle Scholar