Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
SATOH, Junya
1994.
Construction of <i>q</i>-analogue by using Stirling numbers.
Japanese journal of mathematics. New series,
Vol. 20,
Issue. 1,
p.
73.
Tsumura, Hirofumi
1994.
On a q-analogue of the log-Γ-function.
Nagoya Mathematical Journal,
Vol. 134,
Issue. ,
p.
57.
Satoh, Junya
1999.
Sums of Products of Twoq-Bernoulli Numbers.
Journal of Number Theory,
Vol. 74,
Issue. 2,
p.
173.
Satoh, Junya
2000.
A recurrence formula for q-Bernoulli numbers attached to formal group.
Nagoya Mathematical Journal,
Vol. 157,
Issue. ,
p.
93.
Simsek, Yilmaz
2005.
q-Analogue of twisted l-series and q-twisted Euler numbers.
Journal of Number Theory,
Vol. 110,
Issue. 2,
p.
267.
Simsek, Yilmaz
2012.
Generating Functions for q-Apostol Type Frobenius–Euler Numbers and Polynomials.
Axioms,
Vol. 1,
Issue. 3,
p.
395.
Simsek, Yilmaz
Bayad, Abdelmejid
and
Lokesha, V.
2012.
q‐Bernstein polynomials related to q‐Frobenius–Euler polynomials, l‐functions, and q‐Stirling numbers.
Mathematical Methods in the Applied Sciences,
Vol. 35,
Issue. 8,
p.
877.
Yasmin, Ghazala
Islahi, Hibah
and
Choi, Junesang
2021.
q-Generalized Tangent Based Hybrid Polynomials.
Symmetry,
Vol. 13,
Issue. 5,
p.
791.
Kucukoglu, Irem
2022.
Computational and implementational analysis of generating functions for higher order combinatorial numbers and polynomials attached to Dirichlet characters.
Mathematical Methods in the Applied Sciences,
Vol. 45,
Issue. 9,
p.
5043.
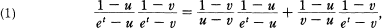
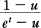 means the generating function of Euler numbers associated to u. So we must extend the above equation to the generating function of q-Euler numbers for our purpose.
means the generating function of Euler numbers associated to u. So we must extend the above equation to the generating function of q-Euler numbers for our purpose.