Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orlik, Peter
and
Terao, Hiroaki
1995.
Arrangements and Milnor fibers.
Mathematische Annalen,
Vol. 301,
Issue. 1,
p.
211.
Forge, David
and
Las Vergnas, Michel
2001.
Orlik–Solomon Type Algebras.
European Journal of Combinatorics,
Vol. 22,
Issue. 5,
p.
699.
Terao, Hiroaki
2002.
Algebras Generated by Reciprocals of Linear Forms.
Journal of Algebra,
Vol. 250,
Issue. 2,
p.
549.
Forge, David
2002.
Bases in Orlik–Solomon Type Algebras.
European Journal of Combinatorics,
Vol. 23,
Issue. 5,
p.
567.
Horiuchi, Hiroki
and
Terao, Hiroaki
2003.
The Poincaré series of the algebra of rational functions which are regular outside hyperplanes.
Journal of Algebra,
Vol. 266,
Issue. 1,
p.
169.
Berget, Andrew
2010.
Products of linear forms and Tutte polynomials.
European Journal of Combinatorics,
Vol. 31,
Issue. 7,
p.
1924.
Schenck, H.
2010.
Resonance Varieties Via Blowups of P2 and Scrolls.
International Mathematics Research Notices,
Ardila, Federico
and
Postnikov, Alexander
2010.
Combinatorics and geometry of power ideals.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 8,
p.
4357.
Holtz, Olga
and
Ron, Amos
2011.
Zonotopal algebra.
Advances in Mathematics,
Vol. 227,
Issue. 2,
p.
847.
Lenz, Matthias
2012.
Hierarchical zonotopal power ideals.
European Journal of Combinatorics,
Vol. 33,
Issue. 6,
p.
1120.
Schenck, Hal
and
Sidman, Jessica
2013.
Commutative Algebra.
p.
639.
Van Le, Dinh
and
Römer, Tim
2013.
Broken circuit complexes and hyperplane arrangements.
Journal of Algebraic Combinatorics,
Vol. 38,
Issue. 4,
p.
989.
Denham, Graham
Garrousian, Mehdi
and
Tohǎneanu, Ştefan O.
2014.
Modular Decomposition of the Orlik-Terao Algebra.
Annals of Combinatorics,
Vol. 18,
Issue. 2,
p.
289.
Le, Dinh Van
2014.
On the Gorensteinness of broken circuit complexes and Orlik–Terao ideals.
Journal of Combinatorial Theory, Series A,
Vol. 123,
Issue. 1,
p.
169.
Aomoto, Kazuhiko
and
Machida, Yoshinori
2015.
Some problems of hypergeometric integrals associated with hypersphere arrangement.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 91,
Issue. 6,
Garrousian, Mehdi
and
Tohǎneanu, Ştefan O.
2015.
Minimum distance of linear codes and the α-invariant.
Advances in Applied Mathematics,
Vol. 71,
Issue. ,
p.
190.
Le, Dinh Van
and
Mohammadi, Fatemeh
2015.
On the Orlik–Terao ideal and the relation space of a hyperplane arrangement.
Advances in Applied Mathematics,
Vol. 71,
Issue. ,
p.
34.
Juhnke-Kubitzke, Martina
and
Le, Dinh Van
2016.
Flawlessness ofh-vectors of broken circuit complexes.
International Mathematics Research Notices,
p.
rnw284.
Lenz, Matthias
2016.
Splines, lattice points, and arithmetic matroids.
Journal of Algebraic Combinatorics,
Vol. 43,
Issue. 2,
p.
277.
Lenz, Matthias
2016.
Zonotopal algebra and forward exchange matroids.
Advances in Mathematics,
Vol. 294,
Issue. ,
p.
819.


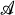 is a finite collection of hyperplanes in
is a finite collection of hyperplanes in 