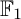 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANSPublished online by Cambridge University Press: 13 December 2023
A quiver representation assigns a vector space to each vertex, and a linear map to each arrow of a quiver. When one considers the category 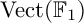 $\mathrm {Vect}(\mathbb {F}_1)$ of vector spaces “over
$\mathrm {Vect}(\mathbb {F}_1)$ of vector spaces “over 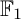 $\mathbb {F}_1$” (the field with one element), one obtains
$\mathbb {F}_1$” (the field with one element), one obtains 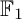 $\mathbb {F}_1$-representations of a quiver. In this paper, we study representations of a quiver over the field with one element in connection to coefficient quivers. To be precise, we prove that the category
$\mathbb {F}_1$-representations of a quiver. In this paper, we study representations of a quiver over the field with one element in connection to coefficient quivers. To be precise, we prove that the category 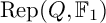 $\mathrm {Rep}(Q,\mathbb {F}_1)$ is equivalent to the (suitably defined) category of coefficient quivers over Q. This provides a conceptual way to see Euler characteristics of a class of quiver Grassmannians as the number of “
$\mathrm {Rep}(Q,\mathbb {F}_1)$ is equivalent to the (suitably defined) category of coefficient quivers over Q. This provides a conceptual way to see Euler characteristics of a class of quiver Grassmannians as the number of “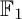 $\mathbb {F}_1$-rational points” of quiver Grassmannians. We generalize techniques originally developed for string and band modules to compute the Euler characteristics of quiver Grassmannians associated with
$\mathbb {F}_1$-rational points” of quiver Grassmannians. We generalize techniques originally developed for string and band modules to compute the Euler characteristics of quiver Grassmannians associated with 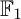 $\mathbb {F}_1$-representations. These techniques apply to a large class of
$\mathbb {F}_1$-representations. These techniques apply to a large class of 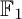 $\mathbb {F}_1$-representations, which we call the
$\mathbb {F}_1$-representations, which we call the 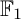 $\mathbb {F}_1$-representations with finite nice length: we prove sufficient conditions for an
$\mathbb {F}_1$-representations with finite nice length: we prove sufficient conditions for an 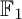 $\mathbb {F}_1$-representation to have finite nice length, and classify such representations for certain families of quivers. Finally, we explore the Hall algebras associated with
$\mathbb {F}_1$-representation to have finite nice length, and classify such representations for certain families of quivers. Finally, we explore the Hall algebras associated with 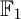 $\mathbb {F}_1$-representations of quivers. We answer the question of how a change in orientation affects the Hall algebra of nilpotent
$\mathbb {F}_1$-representations of quivers. We answer the question of how a change in orientation affects the Hall algebra of nilpotent 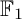 $\mathbb {F}_1$-representations of a quiver with bounded representation type. We also discuss Hall algebras associated with representations with finite nice length, and compute them for certain families of quivers.
$\mathbb {F}_1$-representations of a quiver with bounded representation type. We also discuss Hall algebras associated with representations with finite nice length, and compute them for certain families of quivers.