Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Byeon, Dongho
1996.
Class number one problem for pure cubic fields of Rudman-Stender type.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 72,
Issue. 7,
LOUBOUTIN, Stéphane
1997.
Class-group problems for cubic number fields.
Japanese journal of mathematics. New series,
Vol. 23,
Issue. 2,
p.
365.
Meyer, Andreas
Neis, Stefan
and
Pfahler, Thomas
2001.
Information Security and Privacy.
Vol. 2119,
Issue. ,
p.
84.
Louboutin, Stéphane R.
2006.
The class-number one problem for some real cubic number fields with negative discriminants.
Journal of Number Theory,
Vol. 121,
Issue. 1,
p.
30.
Park, S.-M.
and
Lee, G.-N.
2009.
The class number one problem for some totally complex quartic number fields.
Journal of Number Theory,
Vol. 129,
Issue. 6,
p.
1338.
Godinho, Hemar
Porto, Thiago
and
Togbé, Alain
2014.
On the diophantine equation v(v+1)=u(u+a)(u+2a).
Acta Mathematica Hungarica,
Vol. 143,
Issue. 1,
p.
249.
Zhou, Haiyan
and
Liang, Zhibin
2018.
Tame kernels of cubic and sextic fields.
Journal of Number Theory,
Vol. 190,
Issue. ,
p.
277.
Kala, Vítězslav
and
Tinková, Magdaléna
2023.
Universal Quadratic Forms, Small Norms, and Traces in Families of Number Fields.
International Mathematics Research Notices,
Vol. 2023,
Issue. 9,
p.
7541.
Tinková, Magdaléna
2023.
Trace and norm of indecomposable integers in cubic orders.
The Ramanujan Journal,
Vol. 61,
Issue. 4,
p.
1121.
Benamara, Jamal
2025.
Class number and fundamental units of certain pure cubic fields.
Boletim da Sociedade Paranaense de Matemática,
Vol. 43,
Issue. ,


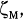 , A
, A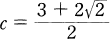 If
If 