Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ponomarev, Paul
1984.
The Doi-Naganuma lifting of quaternary theta series.
Mathematische Annalen,
Vol. 255,
Issue. 4,
p.
443.
Hung, D.C
1987.
Theta series of ternary quadratic forms.
Journal of Number Theory,
Vol. 26,
Issue. 1,
p.
1.
Ponomarev, Paul
1988.
Eichler commutation relations for theta series of nebentypus.
Mathematische Annalen,
Vol. 280,
Issue. 4,
p.
691.
Takada, Ichiro
1990.
On the genera and the class number of unimodular lattices over the ring of integers in real quadratic fields.
Journal of Number Theory,
Vol. 36,
Issue. 3,
p.
373.
Scharlau, Rudolf
1994.
Unimodular lattices over real quadratic fields.
Mathematische Zeitschrift,
Vol. 216,
Issue. 1,
p.
437.


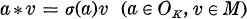 ; the new bilinear form
; the new bilinear form