Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T23:53:24.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Circular Slit Disk with Infinite Radius

Published online by Cambridge University Press:  22 January 2016

Kótaro Oikawa  and
Nobuyuki Suita
Kótaro Oikawa
Affiliation:
College of General Education, University of Tokyo and Department of Mathematics, Tokyo Institute of Technology
Nobuyuki Suita
Affiliation:
College of General Education, University of Tokyo and Department of Mathematics, Tokyo Institute of Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let W be a plane domain such that ∞∉W. Given a point a∉W and a boundary component C of W, consider the family 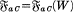consisting of all the functions f satisfying the following conditions: f is regular and univalent in W, f(a) = 0, f′(a) = l, and the image f(C) of C under f is the outer boundary component of the image domain f(W). Set

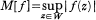
and

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 30 , August 1967 , pp. 57 - 70
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Ahlfors, L.V. and Sario, L. Riemann Surfaces. Princeton Univ. Press, 1960.Google Scholar
[2] Constantinescu, C. Ideale Randkomponenten einer Riemannschen Fläche. Revue Math. Pur. et Appl. 4 (1959), 43–76.Google Scholar
[3] Grötzsch, H. Über die Verzerrung bei schlichter konformer Abbildung mehrfach zusam-menhängender schlichter Bereiche. Sächsiche Akad. Wiss., Berichte, 81 (1929), 38–47.Google Scholar
[4] Grötzsch, H. Eine Bemerkung zum Koebeschen Kreisnormierungsprinzip. Ibid. 87 (1935), 319–324.Google Scholar
[5] Jenkins, J.A. Univalent Functions and Conformal Mapping. Springer Verlag, 1958.Google Scholar
[6] Oikawa, K. Minimal slit regions and linear operator method. Kōdai Math. Sem. Rep. 17 (1965), 187–190.Google Scholar
[7] Reich, E. and Warschawski, S.E. On canonical conformal maps of regions of arbitrary connectivity. Pacific J. 10 (1960), 965–985.Google Scholar
[8] Reich, E. and Warschawski, , Canonical conformal maps onto a circular slit annulus. Scripta Math. 25 (1960), 137–146.Google Scholar
[9] Sario, L. A linear operator method on arbitrary Riemann surfaces. Trans. Amer. Math. Soc. 72 (1952), 281–295.CrossRefGoogle Scholar
[10] Sario, L. Strong and weak boundary components. J. Anal. Math. 5 (1956/57), 389–398.Google Scholar
[11] Suita, N. Minimal slit domains and minimal sets. Kōdai Math. Sem. Rep. 17 (1965), 166–186.Google Scholar
[12] Teichmüller, O. Untersuchungen über konforme und quasikonforme Abbildung. Deutsche Math., 3 (1938), 621–678.Google Scholar