Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harris, Morton E.
1972.
A Characterization of Odd Order Extensions of the Finite Simple Groups PSp(4, q), G2(q), .
Nagoya Mathematical Journal,
Vol. 45,
Issue. ,
p.
79.
Fong, Paul
and
Seitz, Gary M.
1973.
Groups with a (B, N)-pair of rank 2. I.
Inventiones Mathematicae,
Vol. 21,
Issue. 1-2,
p.
1.
Aschbacher, Michael
2002.
Finite groups of G2(3)-type.
Journal of Algebra,
Vol. 257,
Issue. 2,
p.
197.
Michler, Gerhard O.
and
Wang, Lizhong
2011.
Another Uniqueness Proof of the Dickson Simple Group G2(3).
Algebra Colloquium,
Vol. 18,
Issue. 02,
p.
181.


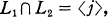 ,
, 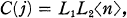 where n
where n