Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:28:18.165Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of complete Riemannian manifolds minimally immersed in the unit sphere*

Published online by Cambridge University Press:  22 January 2016

Qing-Ming Cheng
Qing-Ming Cheng*
Affiliation:
Institute of Mathematics Fudan University, Shanghai P.R., China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Mn be an n-dimensional Riemannian manifold minimally immersed in the unit sphere Sn+p (1) of dimension n + p. When Mn is compact, Chern, do Carmo and Kobayashi [1] proved that if the square ‖h‖2 of length of the second fundamental form h in Mn is not more than 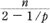, then either Mn is totally

geodesic, or Mn is the Veronese surface in S4 (1) or Mn is the Clifford torus .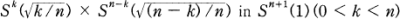

In this paper, we generalize the results due to Chern, do Carmo and Kobayashi [1] to complete Riemannian manifolds.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 131 , September 1993 , pp. 127 - 133
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

Footnotes

*)

Partially supported by the SNF, Ges. Nr. 21-27687. 89

*

The project Supported by NNSFC.

References

[1] Chern, S.S., do Carmo, M. and Kobayashi, S., Minimal submanifolds of a sphere with second fundamental form of constant length, Functional analysis and related fields, (1970), 60–75.Google Scholar
[2] Leung, P.F., Minimal submanifolds in a sphere, Math. Z. 183 (1983), 86–75.CrossRefGoogle Scholar
[3] Yan, S.T., Harmonic functions on complete Riemannian manifolds, Comm. Pure and Appl. Math. 28 (1975), 201–228.Google Scholar