Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tsuchiya, Akihiro
1971.
Characteristic classes for 𝑃𝐿 micro bundles.
Bulletin of the American Mathematical Society,
Vol. 77,
Issue. 4,
p.
531.
Ravenel, Douglas C.
1972.
A definition of exotic characteristic classes of spherical fibrations.
Commentarii Mathematici Helvetici,
Vol. 47,
Issue. 1,
p.
421.
Becker, J. C.
and
Schultz, R. E.
1974.
Equivariant function spaces and stable homotopy theory I.
Commentarii Mathematici Helvetici,
Vol. 49,
Issue. 1,
p.
1.
Cohen, Fred
1976.
The Homology of Iterated Loop Spaces.
Vol. 533,
Issue. ,
p.
352.
May, J. P.
1976.
The Homology of Iterated Loop Spaces.
Vol. 533,
Issue. ,
p.
69.
May, J. P.
1977.
Infinite loop space theory.
Bulletin of the American Mathematical Society,
Vol. 83,
Issue. 4,
p.
456.
Mann, Benjamin Michael
1978.
The cohomology of the symmetric groups.
Transactions of the American Mathematical Society,
Vol. 242,
Issue. 0,
p.
157.
Singh, Neeta
1991.
On topological and homotopy invariance of integral Pontrjagin classes modulo a prime p.
Topology and its Applications,
Vol. 38,
Issue. 3,
p.
225.
Singh, Neeta
1996.
On tertiary exotic characteristic classes.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 8,
p.
2561.
Mimura, Mamoru
1999.
History of Topology.
p.
863.
Castellana, Natàlia
2006.
On the 𝑝-compact groups corresponding to the 𝑝-adic reflection groups 𝐺(𝑞,𝑟,𝑛).
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 7,
p.
2799.
Beardsley, Jonathan
and
Morava, Jack
2018.
Toward a Galois theory of the integers over the sphere spectrum.
Journal of Geometry and Physics,
Vol. 131,
Issue. ,
p.
41.
Beaudry, Agnès
Goerss, Paul G.
Hopkins, Michael J.
and
Stojanoska, Vesna
2022.
Dualizing spheres for compact p-adic analytic groups and duality in chromatic homotopy.
Inventiones mathematicae,
Vol. 229,
Issue. 3,
p.
1301.


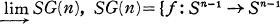 , and
, and 