Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T20:27:53.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Central extensions and rational quadratic forms

Published online by Cambridge University Press:  22 January 2016

Yoshiomi Furuta  and
Tomio Kubota
Yoshiomi Furuta
Affiliation:
Department of Mathematics, Faculty of Science, Kanazawa UniversityKanazawa 920, Japan
Tomio Kubota
Affiliation:
Department of Mathematics, School of Science, Nagoya UniversityChikusa-ku, Nagoya 464-01, Japan, Department of Mathematics, Meijo University, Nagoya, 468, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to characterize by means of simple quadratic forms the set of rational primes that are decomposed completely in a non-abelian central extension which is abelian over a quadratic field. More precisely, let L = Q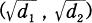 be a bicyclic biquadratic field, and let K = Q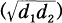. Denote by 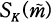the ray class field mod m of K in narrow sense for a large rational integer m. Let 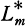be the maximal abelian extension over Q contained in 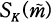and 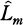be the maximal extension contained in 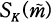such that Gal(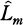/L) is contained in the center of Gal(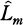/Q). Then we shall show in Theorem 2.1 that any rational prime p not dividing d1d2m is decomposed completely in 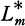/Q if and only if p is representable by rational integers x and y such that x ≡ 1 and y ≡ 0 mod m as follows

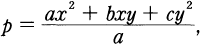
where a, b, c are rational integers such that b2 − 4ac is equal to the discriminant of K and (a) is a norm of a representative of the ray class group of K mod m.

Moreover 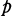is decomposed completely in 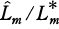if and only if .

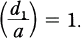Type
Research Article
Information
Nagoya Mathematical Journal , Volume 130 , June 1993 , pp. 177 - 182
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[1] Furuta, Y., Note on class number factors and prime decompositions, Nagoya Math. J., 66(1977), 167–182.CrossRefGoogle Scholar
[2] Furuta, Y., A prime decomposition symbol for a non-abelian central extension which is abelian over a bicyclic biquadratic field, Nagoya Math. J., 79 (1980), 79–109.Google Scholar
[3] Furuta, Y., A norm residue map for central extensions of an algebraic number field, Nagoya Math. J., 93 (1984), 61–69.Google Scholar
[4] Furuta, Y., Gauss’s ternary form reduction and its application to a prime decomposition symbol, Nagoya Math. J., 98 (1985), 77–86.Google Scholar