Article contents
Capacité d’Ensembles de Cantor Généralisés*
Published online by Cambridge University Press: 22 January 2016
Extract
D’abord nous définissons les ensembles de Cantor généralisés. Soient k1, k2, … des nombres entiers supérieurs à 1 et soient p1, p2, … des nombres finis quelconques également supérieurs à 1. On pose lq=l/(kqpq). Soit I un intervalle de longueur d > 0. On enlève de I (kq — l) intervalles de même longueur tels qu’il reste kq intervalles de même longueur lqd. On appelle cette opération la q-opération appliquée à I. On commence par appliquer l’1-opération à [0,1], on applique la 2-opération à chacun des intervalles 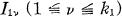 qui restent, puis on applique la 3-opération à chacun des intervalles
qui restent, puis on applique la 3-opération à chacun des intervalles 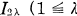
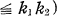 qui restent, et ainsi de suite. On appellera l’ensemble limite restant un ensemble de Cantor généralisé dans E1 et le notera F = F(kq, pq). Notre définition dans En = {(x1, …, xn)}, l’espace euclidien à n dimensions (n ≧ 2), est la suivante: Soit
qui restent, et ainsi de suite. On appellera l’ensemble limite restant un ensemble de Cantor généralisé dans E1 et le notera F = F(kq, pq). Notre définition dans En = {(x1, …, xn)}, l’espace euclidien à n dimensions (n ≧ 2), est la suivante: Soit 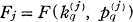 un ensemble de Cantor généralisé défini sur l’axe de xj; nous appellerons l’ensemble produit F = F1 × … × Fn un ensemble de Cantor généralisé dans En (n ≧ 2). II sera appelé symétrique si F1 = … =Fn.
un ensemble de Cantor généralisé défini sur l’axe de xj; nous appellerons l’ensemble produit F = F1 × … × Fn un ensemble de Cantor généralisé dans En (n ≧ 2). II sera appelé symétrique si F1 = … =Fn.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1957
Footnotes
Ce travail avait été annoncé dans la note de bas de page 16 de [4], mais depuis ce temps-là certaines améliorations ont été faites.
References
- 15
- Cited by


