Article contents
Canonical Connections and Pontrjagin Classes
Published online by Cambridge University Press: 22 January 2016
Extract
In the previous paper [7], we have studied the relationship between the Riemannian connection of an n-dimensional Riemannian space M imbedded into the (n + k)-dimensional Euclidean space Rn+k and the canonical connection in the bundle Pn, k = O(n + k)/{l} Х O(k) over the Grassmann manifold Mn, k = O(n + k)/O(n) Х O(k).
In the first half of the present paper, the relationship between the canonical connections in bundles 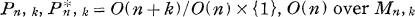 and the invariant Riemannian connection on Mn, k will be discussed. We obtain the holonomy groups of these canonical connections.
and the invariant Riemannian connection on Mn, k will be discussed. We obtain the holonomy groups of these canonical connections.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1957
References
- 2
- Cited by


