Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T23:38:19.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for the cohomology and the Castelnuovo regularity of certain surfaces

Published online by Cambridge University Press:  22 January 2016

M. Brodmann  and
W. Vogel
M. Brodmann
Affiliation:
Mathematisches Institut der Universität, Rämis trasse 74 8001 Zurich, Switzerland
W. Vogel
Affiliation:
Department of Mathematics Massey University, Private Bag Palmerston North, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X ⊆ Pr be a reduced, irreducible and non-degenerate projective variety over an algebraically closed field K of characteristic 0. Let reg(x) be the Castelnuovo-Mumford regularity of the sheaf of ideals 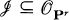associated to X.

Then it is an open problem—due to D. Eisenbud (see e.g. [E-Go])—whether

(0.1) reg(X) ≤ deg(x) - codim (x) + 1,

where deg(x) denotes the degree of X and codim(x) denotes the codimension of X. In many cases, this inequality has been proven to hold true.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 131 , September 1993 , pp. 109 - 126
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[Br] Brodmann, M., Bounds on the cohomological Hilbert functions of a projective variety, J. Algebra, 109 (1987), 352–380.CrossRefGoogle Scholar
[Br2] Brodmann, M., Sectional genus and cohomology of projective varieties, Math. Zeitschr., 208 (1991) 101–126.Google Scholar
[E-Go] Eisenbud, D., Goto, S., Linear resolutions and minimal multiplicity, J. Algebra, 88 (1984), 89–133.Google Scholar
[Ev-Gr] Evans, E. G. Jr., Griffiths, P. A., Local cohomology modules for normal domains, J. London Math. Soc., 19 (1979), 277–284.CrossRefGoogle Scholar
[F-V] Flenner, H., Vogel, W., Connectivity and its Applications to Improper Intersections in P, Math. Gottingensis, Heft 53, Göttingen 1988.Google Scholar
[Fi-V] Fiorentini, M., Vogel, W., Old and New Results and Problems on Buchsbaum Modules, I*, Semin Geom., Univ. Studi Bologna 1988-1991, 53–61, Bologna 1991.Google Scholar
[Go] Goto, S., A Note on quasi-Buchsbaum Rings, Proc. Amer. Math. Soc., 90, (1984), 511–516.CrossRefGoogle Scholar
[G-L-P] Gruson, L., Lazarsfeld, R., Peskine, C., On a theorem of Castelnuovo and the equations defining space curves, Invent. Math., 72 (1983), 491 — 506.CrossRefGoogle Scholar
[H] Harris, J., The genus of space curves, Math. Ann., 249 (1980), 191–204.Google Scholar
[Ho-M-V] Hoa, T., Miro-Roig, R., Vogel, W., On numerical invariants of locally Cohen-Macaulay Schemes in P n , Preprint, MPI/0-57.Google Scholar
[Ho-St-V] Hoa, T., Stückrad, J., Vogel, W., Towards a structure theory for projective varieties of degree = codimension + 2, J. Pure Appl. Algebra, 71 (1991), 203–231.Google Scholar
[Ho-V] Hoa, T., Vogel, W., Castelnuovo-Mumford regularity and hyperplane sections, to appear in Algebra, J..CrossRefGoogle Scholar
[L] Lazarsfeld, R., A sharp Castelnuovo bound for smooth surfaces, Duke Math. J., 55 (1987), 423–429.CrossRefGoogle Scholar
[Mu] Mumford, D., Pathologies III, Amer. J. Math. 89 (1967), 94–104.Google Scholar
[Mu2] Mumford, D., Lectures on Curves on an Algebraic Surface, Annals of Math. Studies No 59, Princeton Univ. Press 1966.Google Scholar
[N] Nagel, U., Uber Gradschranken fiir Syzygien and kohomologische Hilbert-funktionen, Diss. Univ. Paderborn, 1990.Google Scholar
[St-V1] Stückrad, J., Vogel, W., Castelnuovo bounds for certain subvarieties of P n , Math. Ann., 276 (1987), 341–352.Google Scholar
[St-V2] Stückrad, J., Vogel, W., Castelnuovo’s regularity and cohomological properties of sets of points in P n , Math. Ann., 284 (1989), 487–501.CrossRefGoogle Scholar