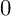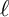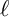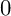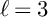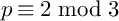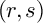1 Introduction
Suppose Y is a smooth projective connected curve of genus g defined over an algebraically closed field k of characteristic
![]() $p>0$
. The p-rank of Y is the integer f such that
$p>0$
. The p-rank of Y is the integer f such that
![]() $p^f$
is the number of p-torsion points of the Jacobian of Y. It is known that
$p^f$
is the number of p-torsion points of the Jacobian of Y. It is known that
![]() $0 \leq f \leq g$
.
$0 \leq f \leq g$
.
Let
![]() $g \geq 2$
. Consider the moduli space
$g \geq 2$
. Consider the moduli space
![]() ${\mathcal M}_g$
of smooth curves of genus g over k and its Deligne–Mumford compactification
${\mathcal M}_g$
of smooth curves of genus g over k and its Deligne–Mumford compactification
![]() $\overline {{\mathcal M}}_g$
. Consider the boundary
$\overline {{\mathcal M}}_g$
. Consider the boundary
![]() $\delta {\mathcal M}_g = \overline {{\mathcal M}}_g - {\mathcal M}_g$
of
$\delta {\mathcal M}_g = \overline {{\mathcal M}}_g - {\mathcal M}_g$
of
![]() ${\mathcal M}_g$
; its points represent singular stable curves of genus g.
${\mathcal M}_g$
; its points represent singular stable curves of genus g.
It is a compelling problem to understand the geometry of the p-rank f stratum
![]() $\overline {{\mathcal M}}_g^f$
of
$\overline {{\mathcal M}}_g^f$
of
![]() $\overline {{\mathcal M}}_g$
. For example, in most cases, it is not known whether
$\overline {{\mathcal M}}_g$
. For example, in most cases, it is not known whether
![]() $\overline {{\mathcal M}}_g^f$
is irreducible.
$\overline {{\mathcal M}}_g^f$
is irreducible.
It is known, by [Reference Faber and van der Geer10, Th. 2.3], that every irreducible component of
![]() $\overline {{\mathcal M}}_g^f$
has dimension
$\overline {{\mathcal M}}_g^f$
has dimension
![]() $2g- 3 + f$
. By [Reference Achter and Pries4, Lem. 3.2], every irreducible component of
$2g- 3 + f$
. By [Reference Achter and Pries4, Lem. 3.2], every irreducible component of
![]() $\overline {{\mathcal M}}_g^f$
contains an open dense subset which lies in
$\overline {{\mathcal M}}_g^f$
contains an open dense subset which lies in
![]() ${\mathcal M}_g^f$
. It follows that there exists a smooth curve of genus g and p-rank f defined over
${\mathcal M}_g^f$
. It follows that there exists a smooth curve of genus g and p-rank f defined over
![]() $\overline {\mathbb F}_p$
for every prime p and pair of integers g and f such that
$\overline {\mathbb F}_p$
for every prime p and pair of integers g and f such that
![]() $0 \leq f \leq g$
.
$0 \leq f \leq g$
.
The proof of [Reference Faber and van der Geer10, Th. 2.3] uses properties of the intersection of the p-rank strata with the boundary. By [Reference Faber and van der Geer10, Lem. 2.5] (see also [Reference Achter and Pries4, Cor. 3.6]), every irreducible component
![]() ${\mathcal S}$
of the p-rank
${\mathcal S}$
of the p-rank
![]() $0$
stratum
$0$
stratum
![]() $\overline {{\mathcal M}}_g^0$
intersects
$\overline {{\mathcal M}}_g^0$
intersects
![]() $\delta {\mathcal M}_g$
; specifically:
$\delta {\mathcal M}_g$
; specifically:
(i)
![]() ${\mathcal S}$
contains points that represent chains of g (supersingular) elliptic curves and
${\mathcal S}$
contains points that represent chains of g (supersingular) elliptic curves and
(ii)
![]() ${\mathcal S}$
intersects every irreducible component of
${\mathcal S}$
intersects every irreducible component of
![]() $\delta {\mathcal M}_g$
.
$\delta {\mathcal M}_g$
.
Analogously, for odd p, one can study the p-rank f stratum
![]() $\overline {{\mathcal H}}_g^f$
of the moduli space
$\overline {{\mathcal H}}_g^f$
of the moduli space
![]() ${\mathcal H}_g$
of hyperelliptic curves of genus g. By [Reference Glass and Pries11, Prop. 2], every irreducible component of
${\mathcal H}_g$
of hyperelliptic curves of genus g. By [Reference Glass and Pries11, Prop. 2], every irreducible component of
![]() $\overline {{\mathcal H}}_g^f$
has dimension
$\overline {{\mathcal H}}_g^f$
has dimension
![]() $g-1+f$
. Every irreducible component of
$g-1+f$
. Every irreducible component of
![]() $\overline {{\mathcal H}}_g^f$
contains an open dense subset which lies in
$\overline {{\mathcal H}}_g^f$
contains an open dense subset which lies in
![]() ${\mathcal H}_g^f$
[Reference Achter and Pries5, Lem. 3.2]. It follows that there exists a smooth hyperelliptic curve of genus g and p-rank f defined over
${\mathcal H}_g^f$
[Reference Achter and Pries5, Lem. 3.2]. It follows that there exists a smooth hyperelliptic curve of genus g and p-rank f defined over
![]() $\overline {\mathbb F}_p$
for every odd prime p and pair of integers g and f such that
$\overline {\mathbb F}_p$
for every odd prime p and pair of integers g and f such that
![]() $0 \leq f \leq g$
.
$0 \leq f \leq g$
.
The proof of these facts for the hyperelliptic locus also uses the intersection of the p-rank strata with the boundary
![]() $\delta {\mathcal H}_g = \overline {{\mathcal H}}_g - {\mathcal H}_g$
. Every irreducible component
$\delta {\mathcal H}_g = \overline {{\mathcal H}}_g - {\mathcal H}_g$
. Every irreducible component
![]() ${\mathcal S}$
of the p-rank
${\mathcal S}$
of the p-rank
![]() $0$
stratum
$0$
stratum
![]() $\overline {{\mathcal H}}_g^0$
intersects
$\overline {{\mathcal H}}_g^0$
intersects
![]() $\delta {\mathcal H}_g$
by [Reference Achter and Pries5, Th. 3.11]; specifically:
$\delta {\mathcal H}_g$
by [Reference Achter and Pries5, Th. 3.11]; specifically:
(i)’
![]() ${\mathcal S}$
contains points that represent trees of g (supersingular) elliptic curves.
${\mathcal S}$
contains points that represent trees of g (supersingular) elliptic curves.
However, it is not known whether
![]() ${\mathcal S}$
intersects every irreducible component of
${\mathcal S}$
intersects every irreducible component of
![]() $\delta {\mathcal H}_g$
.
$\delta {\mathcal H}_g$
.
In this paper, for an odd prime
![]() $\ell $
with
$\ell $
with
![]() $\ell \not = p$
, we study analogous questions about the p-ranks of curves that admit a
$\ell \not = p$
, we study analogous questions about the p-ranks of curves that admit a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover of the projective line
$\mathbb {Z}/\ell \mathbb {Z}$
-cover of the projective line
![]() ${\mathbb P}^1$
. Let
${\mathbb P}^1$
. Let
![]() ${\mathcal T}_{\ell , g}$
denote the moduli space of such
${\mathcal T}_{\ell , g}$
denote the moduli space of such
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-covers, and let
$\mathbb {Z}/\ell \mathbb {Z}$
-covers, and let
![]() ${\overline {{\mathcal T}}}_{\ell , g}$
denote its compactification. The irreducible components of
${\overline {{\mathcal T}}}_{\ell , g}$
denote its compactification. The irreducible components of
![]() ${\mathcal T}_{\ell , g}$
are indexed not only by the degree
${\mathcal T}_{\ell , g}$
are indexed not only by the degree
![]() $\ell $
and the genus g, but also by the discrete data of the inertia type, which determines the signature type. In Proposition 4.1, we compute a lower bound for the dimension of each irreducible component of the p-rank strata of
$\ell $
and the genus g, but also by the discrete data of the inertia type, which determines the signature type. In Proposition 4.1, we compute a lower bound for the dimension of each irreducible component of the p-rank strata of
![]() ${\mathcal T}_{\ell , g}$
, in terms of the signature type.
${\mathcal T}_{\ell , g}$
, in terms of the signature type.
The first topic we study is how the p-rank
![]() $0$
stratum
$0$
stratum
![]() ${\overline {{\mathcal T}}}_{\ell , g}^0$
of the moduli space
${\overline {{\mathcal T}}}_{\ell , g}^0$
of the moduli space
![]() ${\overline {{\mathcal T}}}_{\ell , g}$
intersects the boundary
${\overline {{\mathcal T}}}_{\ell , g}$
intersects the boundary
![]() $\delta {\mathcal M}_g$
. The first main result of the paper is the following theorem.
$\delta {\mathcal M}_g$
. The first main result of the paper is the following theorem.
Theorem 1.1 [See Theorem 4.3]
Every irreducible component
![]() ${\mathcal S}$
of
${\mathcal S}$
of
![]() ${\overline {{\mathcal T}}}_{\ell , g}^0$
contains a point representing a curve of compact type which has at least
${\overline {{\mathcal T}}}_{\ell , g}^0$
contains a point representing a curve of compact type which has at least
![]() $\mathrm {dim}({\mathcal S}) + 1$
components.
$\mathrm {dim}({\mathcal S}) + 1$
components.
The geometric conclusion from Theorem 1.1 is not as strong as the analogous result in the hyperelliptic case. This prevented us from using Theorem 1.1 to find the dimension of the irreducible components of
![]() ${\mathcal T}_{\ell , g}^f$
in general (see Remark 4.4 and §7.2).
${\mathcal T}_{\ell , g}^f$
in general (see Remark 4.4 and §7.2).
For this reason, in §5, we specialize to the case
![]() $\ell = 3$
. In Proposition 5.9, for all
$\ell = 3$
. In Proposition 5.9, for all
![]() $g \geq 2$
and all primes
$g \geq 2$
and all primes
![]() $p \geq 5$
, we generalize a result of Bouw by proving that every component of the moduli space of trielliptic curves of genus g contains a curve whose p-rank is not the maximum. Then we prove the following theorem.
$p \geq 5$
, we generalize a result of Bouw by proving that every component of the moduli space of trielliptic curves of genus g contains a curve whose p-rank is not the maximum. Then we prove the following theorem.
Theorem 1.2 [See Theorem 5.11]
For every odd
![]() $p \equiv 2 \bmod 3$
, every
$p \equiv 2 \bmod 3$
, every
![]() $g \in \mathbb {N}$
, every trielliptic signature type
$g \in \mathbb {N}$
, every trielliptic signature type
![]() $(r,s)$
for g, and every f (satisfying the clear necessary conditions that f is even and
$(r,s)$
for g, and every f (satisfying the clear necessary conditions that f is even and
![]() $0 \leq f \leq 2\mathrm {min}(r,s)$
), there exists a smooth trielliptic curve defined over
$0 \leq f \leq 2\mathrm {min}(r,s)$
), there exists a smooth trielliptic curve defined over
![]() ${\overline {\mathbb {F}}}_p$
with genus g, signature type
${\overline {\mathbb {F}}}_p$
with genus g, signature type
![]() $(r,s)$
, and p-rank f; furthermore, the dimension of at least one irreducible component of the p-rank f stratum of
$(r,s)$
, and p-rank f; furthermore, the dimension of at least one irreducible component of the p-rank f stratum of
![]() ${\mathcal T}_{3, g, (r,s)}$
equals the lower bound from Proposition 4.1.
${\mathcal T}_{3, g, (r,s)}$
equals the lower bound from Proposition 4.1.
In Corollary 6.4, we strengthen Theorem 1.2 when g is small for all odd primes
![]() $p \equiv 2 \bmod 3$
using an application of Theorem 1.1.
$p \equiv 2 \bmod 3$
using an application of Theorem 1.1.
2 Background
In this section, we include necessary material about cyclic covers and the p-rank.
2.1 Stable
 $\mathbb {Z}/\ell \mathbb {Z}$
-covers of a genus zero curve
$\mathbb {Z}/\ell \mathbb {Z}$
-covers of a genus zero curve
Let k be an algebraically closed field of characteristic
![]() $p> 0$
, and let S be an irreducible scheme over k. Let
$p> 0$
, and let S be an irreducible scheme over k. Let
![]() $G=\mathbb {Z}/\ell \mathbb {Z}$
be a cyclic group of odd prime order
$G=\mathbb {Z}/\ell \mathbb {Z}$
be a cyclic group of odd prime order
![]() $\ell \not = p$
. Let
$\ell \not = p$
. Let
![]() $G^*=G-\{0\}$
.
$G^*=G-\{0\}$
.
Let
![]() $\psi :Y \to S$
be a semi-stable curve. If
$\psi :Y \to S$
be a semi-stable curve. If
![]() $s \in S$
, let
$s \in S$
, let
![]() $Y_s$
denote the fiber of Y over s. Let
$Y_s$
denote the fiber of Y over s. Let
![]() $\mathrm {Sing}_S(Y)$
be the set of
$\mathrm {Sing}_S(Y)$
be the set of
![]() $z \in Y$
for which z is a singular point of the fiber
$z \in Y$
for which z is a singular point of the fiber
![]() $Y_{\psi (z)}$
.
$Y_{\psi (z)}$
.
A mark
![]() $R_\Xi $
on
$R_\Xi $
on
![]() $Y/S$
is a closed subscheme of
$Y/S$
is a closed subscheme of
![]() $Y-\mathrm {Sing}_S(Y)$
which is finite and étale over S. The degree of
$Y-\mathrm {Sing}_S(Y)$
which is finite and étale over S. The degree of
![]() $R_\Xi $
is the number of points in any geometric fiber of
$R_\Xi $
is the number of points in any geometric fiber of
![]() $R_\Xi \to S$
. A marked semi-stable curve
$R_\Xi \to S$
. A marked semi-stable curve
![]() $(Y/S, R_\Xi )$
is stably marked if every geometric fiber of Y satisfies the following condition: for each irreducible component
$(Y/S, R_\Xi )$
is stably marked if every geometric fiber of Y satisfies the following condition: for each irreducible component
![]() $Y_0$
of genus zero,
$Y_0$
of genus zero,
![]() $\# (Y_0 \cap (\mathrm {Sing}_S(Y) \cup R_\Xi )) \ge 3$
. (If the fibers of
$\# (Y_0 \cap (\mathrm {Sing}_S(Y) \cup R_\Xi )) \ge 3$
. (If the fibers of
![]() $Y/S$
have genus
$Y/S$
have genus
![]() $1$
, we also assume that the degree of
$1$
, we also assume that the degree of
![]() $R_\Xi $
is positive.)
$R_\Xi $
is positive.)
Consider a G-action
![]() $\iota _0: G \hookrightarrow \mathrm {Aut}_S(Y)$
on Y. Let R denote the ramification locus of
$\iota _0: G \hookrightarrow \mathrm {Aut}_S(Y)$
on Y. Let R denote the ramification locus of
![]() $Y \to Y/\iota _0(G)$
. The smooth ramification locus is
$Y \to Y/\iota _0(G)$
. The smooth ramification locus is
![]() $R_{\mathrm {sm}} := R - (R\cap \mathrm {Sing}_S(Y))$
. We say that
$R_{\mathrm {sm}} := R - (R\cap \mathrm {Sing}_S(Y))$
. We say that
![]() $(Y/S,\iota _0)$
is a stable G-curve if
$(Y/S,\iota _0)$
is a stable G-curve if
![]() $Y/S$
is a semi-stable curve, if
$Y/S$
is a semi-stable curve, if
![]() $\iota _0: G \hookrightarrow \mathrm {Aut}_S(Y)$
is an action of G, if
$\iota _0: G \hookrightarrow \mathrm {Aut}_S(Y)$
is an action of G, if
![]() $R_{\mathrm {sm}}$
is a mark on
$R_{\mathrm {sm}}$
is a mark on
![]() $Y/S$
, and if
$Y/S$
, and if
![]() $(Y/S,R_{\mathrm {sm}})$
is stably marked.
$(Y/S,R_{\mathrm {sm}})$
is stably marked.
If
![]() $z \in \mathrm {Sing}_S(Y)$
, let
$z \in \mathrm {Sing}_S(Y)$
, let
![]() $Y_{z,1}$
and
$Y_{z,1}$
and
![]() $Y_{z,2}$
denote the two components of the formal completion of
$Y_{z,2}$
denote the two components of the formal completion of
![]() $Y_{\psi (z)}$
at z. A stable G-curve
$Y_{\psi (z)}$
at z. A stable G-curve
![]() $(Y/S, \iota _0)$
is admissible if the following conditions are satisfied for every geometric point
$(Y/S, \iota _0)$
is admissible if the following conditions are satisfied for every geometric point
![]() $z \in R\cap \mathrm {Sing}_S(Y)$
:
$z \in R\cap \mathrm {Sing}_S(Y)$
:
-
1.
 $\iota _0(1)$
stabilizes each branch
$\iota _0(1)$
stabilizes each branch
 $Y_{z,i}$
;
$Y_{z,i}$
; -
2. z is a ramification point of the restriction of
 $\iota _0$
to
$\iota _0$
to
 $Y_{z,i}$
; and
$Y_{z,i}$
; and -
3. the characters of the action of
 $\iota _0$
on the tangent spaces of
$\iota _0$
on the tangent spaces of
 $Y_{z,1}$
and
$Y_{z,1}$
and
 $Y_{z,2}$
at z are inverses.
$Y_{z,2}$
at z are inverses.
Suppose that
![]() $(Y/S, \iota _0)$
is an admissible stable G-curve. Then
$(Y/S, \iota _0)$
is an admissible stable G-curve. Then
![]() $Y/\iota _0(G)$
is also a stably marked curve [Reference Ekedahl8, Prop. 1.4]. The mark on
$Y/\iota _0(G)$
is also a stably marked curve [Reference Ekedahl8, Prop. 1.4]. The mark on
![]() $Y/\iota _0(G)$
is the smooth branch locus
$Y/\iota _0(G)$
is the smooth branch locus
![]() $B_{\mathrm {sm}}$
, which is the (reduced subscheme of) the image of
$B_{\mathrm {sm}}$
, which is the (reduced subscheme of) the image of
![]() $R_{\mathrm {sm}}$
under the morphism
$R_{\mathrm {sm}}$
under the morphism
![]() $Y \to Y/\iota _0(G)$
. Let n be the degree of
$Y \to Y/\iota _0(G)$
. Let n be the degree of
![]() $R_{\mathrm {sm}}$
(the number of smooth ramification points). We suppose from now on that
$R_{\mathrm {sm}}$
(the number of smooth ramification points). We suppose from now on that
![]() $Y/\iota _0(G)$
has arithmetic genus
$Y/\iota _0(G)$
has arithmetic genus
![]() $0$
. By the Riemann–Hurwitz formula, the arithmetic genus of each fiber of Y is
$0$
. By the Riemann–Hurwitz formula, the arithmetic genus of each fiber of Y is
2.2 The inertia type and signature type
Let s be a geometric point of S, and let a be a point of the fiber
![]() $R_{\mathrm {sm},s}$
. Then
$R_{\mathrm {sm},s}$
. Then
![]() $G= \mathbb {Z}/\ell \mathbb {Z}$
acts on the tangent space of
$G= \mathbb {Z}/\ell \mathbb {Z}$
acts on the tangent space of
![]() $Y_s$
at a via a character
$Y_s$
at a via a character
![]() $\chi _a: G \to k^*$
. In particular, there is a unique choice of
$\chi _a: G \to k^*$
. In particular, there is a unique choice of
![]() $\gamma _a \in (\mathbb {Z}/\ell \mathbb {Z})^*$
so that
$\gamma _a \in (\mathbb {Z}/\ell \mathbb {Z})^*$
so that
![]() $\chi _a(1) = \zeta _\ell ^{\gamma _a}$
. We say that
$\chi _a(1) = \zeta _\ell ^{\gamma _a}$
. We say that
![]() $\gamma _a$
is the canonical generator of inertia at a. The inertia type of
$\gamma _a$
is the canonical generator of inertia at a. The inertia type of
![]() $(Y/S,\iota _0)$
is the multiset
$(Y/S,\iota _0)$
is the multiset
![]() ${\overline {\gamma }} = \{\gamma _{a} \mid a \in R_{\mathrm {sm},s}\}$
. It is independent of the choice of s. By Riemann’s existence theorem, there exists a cover
${\overline {\gamma }} = \{\gamma _{a} \mid a \in R_{\mathrm {sm},s}\}$
. It is independent of the choice of s. By Riemann’s existence theorem, there exists a cover
![]() $(Y, \iota _0)$
with inertia type
$(Y, \iota _0)$
with inertia type
![]() $\{\gamma _{a} \mid a \in R_{\mathrm {sm},s}\}$
if and only if
$\{\gamma _{a} \mid a \in R_{\mathrm {sm},s}\}$
if and only if
![]() $\sum _{a \in R_{\mathrm {sm},s}} \gamma _a = 0 \in \mathbb {Z}/\ell \mathbb {Z}$
[Reference Völklein24, Th. 2.13].
$\sum _{a \in R_{\mathrm {sm},s}} \gamma _a = 0 \in \mathbb {Z}/\ell \mathbb {Z}$
[Reference Völklein24, Th. 2.13].
A labeling of a mark
![]() $R_\Xi $
of degree n is a bijection
$R_\Xi $
of degree n is a bijection
![]() $\eta $
between
$\eta $
between
![]() $\{1, \ldots , n\}$
and the irreducible components of
$\{1, \ldots , n\}$
and the irreducible components of
![]() $R_\Xi $
. A labeling of an admissible stable G-curve
$R_\Xi $
. A labeling of an admissible stable G-curve
![]() $(Y/S,\iota _0)$
is a labeling
$(Y/S,\iota _0)$
is a labeling
![]() $\eta $
of
$\eta $
of
![]() $R_{\mathrm {sm}}$
. There is an induced labeling
$R_{\mathrm {sm}}$
. There is an induced labeling
![]() $\eta _0:\{1, \ldots , n\} \to B_{\mathrm {sm}}$
.
$\eta _0:\{1, \ldots , n\} \to B_{\mathrm {sm}}$
.
If
![]() $(Y/S,\iota _0,\eta )$
is a labeled G-curve, the class vector is the map of sets
$(Y/S,\iota _0,\eta )$
is a labeled G-curve, the class vector is the map of sets
![]() $\gamma :\{1, \ldots , n\} \to G^*$
such that
$\gamma :\{1, \ldots , n\} \to G^*$
such that
![]() $\gamma (i) = \gamma _{\eta (i)}$
. We write
$\gamma (i) = \gamma _{\eta (i)}$
. We write
![]() $\gamma = (\gamma (1), \ldots , \gamma (n))$
. If
$\gamma = (\gamma (1), \ldots , \gamma (n))$
. If
![]() $\gamma $
is a class vector, we denote its inertia type by
$\gamma $
is a class vector, we denote its inertia type by
![]() ${\overline {\gamma }}: G^* \to \mathbb {Z}_{\ge 0}$
where
${\overline {\gamma }}: G^* \to \mathbb {Z}_{\ge 0}$
where
![]() ${\overline {\gamma }}(h) = \#\{i \mid 1 \leq i \leq n, \ \gamma (i) = h\}$
for all
${\overline {\gamma }}(h) = \#\{i \mid 1 \leq i \leq n, \ \gamma (i) = h\}$
for all
![]() $h\in G^*$
.
$h\in G^*$
.
Let
![]() $\zeta _{\ell } \in k$
be a primitive
$\zeta _{\ell } \in k$
be a primitive
![]() $\ell $
th root of unity. The automorphism
$\ell $
th root of unity. The automorphism
![]() $\iota _0(1)$
induces an action on
$\iota _0(1)$
induces an action on
![]() $H^0(Y_s, \Omega ^1)$
. Let
$H^0(Y_s, \Omega ^1)$
. Let
![]() $\mathcal {L}_i$
be the
$\mathcal {L}_i$
be the
![]() $\zeta _\ell ^i$
-eigenspace of
$\zeta _\ell ^i$
-eigenspace of
![]() $H^0(Y_s, \Omega ^1)$
, for
$H^0(Y_s, \Omega ^1)$
, for
![]() $0 \leq i \leq \ell -1$
. There is an eigenspace decomposition:
$0 \leq i \leq \ell -1$
. There is an eigenspace decomposition:
Let
![]() $s_i =\mathrm {dim}(\mathcal {L}_i)$
. Then
$s_i =\mathrm {dim}(\mathcal {L}_i)$
. Then
![]() $\mathcal {L}_0=\{0\}$
and
$\mathcal {L}_0=\{0\}$
and
![]() $s_0=0$
since
$s_0=0$
since
![]() $Y/\iota _0(G)$
has genus
$Y/\iota _0(G)$
has genus
![]() $0$
. The signature type is
$0$
. The signature type is
![]() $(s_1, \ldots , s_{\ell -1})$
. It is locally constant on S. For an integer t, let
$(s_1, \ldots , s_{\ell -1})$
. It is locally constant on S. For an integer t, let
![]() $\langle \frac {t}{\ell } \rangle = \frac {t}{\ell } - \lfloor \frac {t}{\ell } \rfloor $
denote the fractional part of
$\langle \frac {t}{\ell } \rangle = \frac {t}{\ell } - \lfloor \frac {t}{\ell } \rfloor $
denote the fractional part of
![]() $\frac {t}{\ell }$
.
$\frac {t}{\ell }$
.
Lemma 2.1. For
![]() $1 \leq i \leq \ell -1$
,
$1 \leq i \leq \ell -1$
,
 $$ \begin{align*} s_i=-1 + \sum\limits_{j=1}^{n} \langle \frac{- i a_j}{\ell} \rangle. \end{align*} $$
$$ \begin{align*} s_i=-1 + \sum\limits_{j=1}^{n} \langle \frac{- i a_j}{\ell} \rangle. \end{align*} $$
Proof. This can be found in [Reference Moonen19, Lem. 2.7, §3.2], or deduced from earlier results [Reference Bouw7, Lem. 4.3] (the negative sign does not appear for the action on
![]() ${\mathcal O}$
) or [Reference Kani13, Prop. 1].
${\mathcal O}$
) or [Reference Kani13, Prop. 1].
2.3 Restrictions on the p-rank
Let
![]() $\mu _p$
be the kernel of Frobenius on
$\mu _p$
be the kernel of Frobenius on
![]() ${\mathbb G}_m$
. The p-rank of a semi-abelian variety
${\mathbb G}_m$
. The p-rank of a semi-abelian variety
![]() $A'$
over k is
$A'$
over k is
![]() $f_{A'}=\mathrm {dim}_{{\mathbb F}_p}\mathrm {Hom}(\mu _p, A')$
. If
$f_{A'}=\mathrm {dim}_{{\mathbb F}_p}\mathrm {Hom}(\mu _p, A')$
. If
![]() $A'$
is an extension of an abelian variety A by a torus T, then
$A'$
is an extension of an abelian variety A by a torus T, then
![]() $f_{A'}=f_A + \mathrm {rank}(T)$
.
$f_{A'}=f_A + \mathrm {rank}(T)$
.
For an abelian variety A, the p-rank can also be defined as the integer
![]() $f_A$
such that the number of p-torsion points in
$f_A$
such that the number of p-torsion points in
![]() $A(k)$
is
$A(k)$
is
![]() $p^{f_A}$
. If A has dimension
$p^{f_A}$
. If A has dimension
![]() $g_A$
, then
$g_A$
, then
![]() $0 \leq f_A \leq g_A$
. The p-rank of a stable curve Y is that of
$0 \leq f_A \leq g_A$
. The p-rank of a stable curve Y is that of
![]() $\mathrm {Pic}^0(Y)$
.
$\mathrm {Pic}^0(Y)$
.
Recall that
![]() $\ell \not = p$
is prime. Let e be the order of p in the multiplicative group
$\ell \not = p$
is prime. Let e be the order of p in the multiplicative group
![]() $(\mathbb Z/ \ell \mathbb Z)^\times $
.
$(\mathbb Z/ \ell \mathbb Z)^\times $
.
Lemma 2.2. Suppose that
![]() $Y \to \mathbb {P}_k^1$
is a
$Y \to \mathbb {P}_k^1$
is a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover. Let f be the p-rank of Y.
$\mathbb {Z}/\ell \mathbb {Z}$
-cover. Let f be the p-rank of Y.
-
1. Then f is divisible by e, the order of p modulo
 $\ell $
.
$\ell $
. -
2. If
 $\ell> 3$
or if
$\ell> 3$
or if
 $\ell =3$
and
$\ell =3$
and
 $p \equiv 1 \bmod 3$
, then
$p \equiv 1 \bmod 3$
, then
 $f \not = g-1$
.
$f \not = g-1$
.
Proof. The action of
![]() $\mathbb {Z}/\ell \mathbb {Z}$
on Y induces an action of
$\mathbb {Z}/\ell \mathbb {Z}$
on Y induces an action of
![]() $\zeta _\ell $
on
$\zeta _\ell $
on
![]() $J=\mathrm {Jac}(Y)$
and its p-divisible group
$J=\mathrm {Jac}(Y)$
and its p-divisible group
![]() $J[p^\infty ]$
. So
$J[p^\infty ]$
. So
![]() $\mathbb {Z}[\zeta _\ell ] \hookrightarrow \mathrm {End}(J[p^\infty ])$
. If
$\mathbb {Z}[\zeta _\ell ] \hookrightarrow \mathrm {End}(J[p^\infty ])$
. If
![]() $(c, d)$
is a pair of relatively prime nonnegative integers, and
$(c, d)$
is a pair of relatively prime nonnegative integers, and
![]() $\lambda =d/(c+d)$
, let
$\lambda =d/(c+d)$
, let
![]() $G_{\lambda }$
denote a p-divisible group of codimension c, dimension d, and thus height
$G_{\lambda }$
denote a p-divisible group of codimension c, dimension d, and thus height
![]() $c + d$
. By [Reference Manin18], the Dieudonné–Manin classification, there is an isogeny of p-divisible groups
$c + d$
. By [Reference Manin18], the Dieudonné–Manin classification, there is an isogeny of p-divisible groups
![]() $J[p^\infty ] \sim \oplus _\lambda G_\lambda ^{m(\lambda )}$
. The action of
$J[p^\infty ] \sim \oplus _\lambda G_\lambda ^{m(\lambda )}$
. The action of
![]() $\zeta _\ell $
stabilizes every slope factor
$\zeta _\ell $
stabilizes every slope factor
![]() $G_{\lambda }^{m(\lambda )}$
of
$G_{\lambda }^{m(\lambda )}$
of
![]() $J[p^\infty ]$
. Hence,
$J[p^\infty ]$
. Hence,
![]() $\mathbb {Z}[\zeta _\ell ] \hookrightarrow \operatorname {\mathrm {End}}(G_\lambda ^{m(\lambda )})$
. If
$\mathbb {Z}[\zeta _\ell ] \hookrightarrow \operatorname {\mathrm {End}}(G_\lambda ^{m(\lambda )})$
. If
![]() $m(\lambda )>0$
, this yields an inclusion
$m(\lambda )>0$
, this yields an inclusion
![]() $\mathbb {Q}(\zeta _\ell ) \otimes \mathbb {Q}_p \hookrightarrow \mathrm {Mat}_{m(\lambda )} (D_{\lambda }) $
where
$\mathbb {Q}(\zeta _\ell ) \otimes \mathbb {Q}_p \hookrightarrow \mathrm {Mat}_{m(\lambda )} (D_{\lambda }) $
where
![]() $D_{\lambda }$
is the
$D_{\lambda }$
is the
![]() $\mathbb {Q}_p$
-division algebra with Brauer invariant
$\mathbb {Q}_p$
-division algebra with Brauer invariant
![]() $\lambda \in \mathbb {Q}/\mathbb {Z}$
.
$\lambda \in \mathbb {Q}/\mathbb {Z}$
.
-
1. If
 $\lambda =0$
, then
$\lambda =0$
, then
 $m(\lambda )=f$
. Let
$m(\lambda )=f$
. Let
 $L_p$
be the completion of
$L_p$
be the completion of
 $L=\mathbb {Q}(\zeta _\ell )$
at a prime lying above p. Then
$L=\mathbb {Q}(\zeta _\ell )$
at a prime lying above p. Then
 $[L_p: \mathbb {Q}_p]=e$
divides
$[L_p: \mathbb {Q}_p]=e$
divides
 $m(\lambda )$
.
$m(\lambda )$
. -
2. Suppose
 $f=g-1$
. Then the slope
$f=g-1$
. Then the slope
 $1/2$
factor of
$1/2$
factor of
 $J[p^\infty ]$
is the p-divisible group of a supersingular elliptic curve. So
$J[p^\infty ]$
is the p-divisible group of a supersingular elliptic curve. So
 $\mathbb {Q}(\zeta _\ell ) \subset E$
where E is the endomorphism algebra of a supersingular elliptic curve. Then E is a quaternion algebra ramified exactly at
$\mathbb {Q}(\zeta _\ell ) \subset E$
where E is the endomorphism algebra of a supersingular elliptic curve. Then E is a quaternion algebra ramified exactly at
 $\infty , p$
. The only number fields contained in E are quadratic fields inert or ramified at p. This gives a contradiction if
$\infty , p$
. The only number fields contained in E are quadratic fields inert or ramified at p. This gives a contradiction if
 $\ell>3$
or if
$\ell>3$
or if
 $\ell =3$
and
$\ell =3$
and
 $p \equiv 1 \bmod 3.$
$p \equiv 1 \bmod 3.$
The p-rank of Y equals the stable rank of the Cartier operator
![]() $\mathbf {C}$
. If
$\mathbf {C}$
. If
![]() $\omega \in H^0(Y, \Omega ^1)$
, then
$\omega \in H^0(Y, \Omega ^1)$
, then
![]() $\mathbf {C}(\zeta _\ell ^{pi} \omega )=\zeta _\ell ^i\mathbf {C}(\omega )$
. Then
$\mathbf {C}(\zeta _\ell ^{pi} \omega )=\zeta _\ell ^i\mathbf {C}(\omega )$
. Then
![]() $\mathbf {C}(\mathcal {L}_i) \subset \mathcal {L}_{\sigma (i)}$
where
$\mathbf {C}(\mathcal {L}_i) \subset \mathcal {L}_{\sigma (i)}$
where
![]() $\sigma $
is the permutation of
$\sigma $
is the permutation of
![]() $\mathbb {Z}/\ell \mathbb {Z}-\{0\}$
which sends i to
$\mathbb {Z}/\ell \mathbb {Z}-\{0\}$
which sends i to
![]() $p^{-1}i$
. The cycle structure of
$p^{-1}i$
. The cycle structure of
![]() $\sigma $
is determined by the splitting of p in
$\sigma $
is determined by the splitting of p in
![]() $\mathbb {Z}[\zeta _{\ell }]$
. Recall that e is the order of p modulo
$\mathbb {Z}[\zeta _{\ell }]$
. Recall that e is the order of p modulo
![]() $\ell $
. There are
$\ell $
. There are
![]() $(\ell -1)/e$
primes of
$(\ell -1)/e$
primes of
![]() $\mathbb {Z}[\zeta _\ell ]$
lying over p with residual degree e. Each orbit of
$\mathbb {Z}[\zeta _\ell ]$
lying over p with residual degree e. Each orbit of
![]() $\mathbf {C}$
on
$\mathbf {C}$
on
![]() $\{\mathcal {L}_i\}$
has cardinality e. Let O denote the set of orbits. The contribution to the p-rank from each of the e eigenspaces in an orbit
$\{\mathcal {L}_i\}$
has cardinality e. Let O denote the set of orbits. The contribution to the p-rank from each of the e eigenspaces in an orbit
![]() $o \in O$
is bounded by the minimum of
$o \in O$
is bounded by the minimum of
![]() $s_i =\mathrm {dim}(\mathcal {L}_i)$
for
$s_i =\mathrm {dim}(\mathcal {L}_i)$
for
![]() $\mathcal {L}_i$
in o.
$\mathcal {L}_i$
in o.
Bouw used these ideas to find an upper bound on the p-rank, which depends only on p,
![]() $\ell $
, and the inertia type
$\ell $
, and the inertia type
![]() ${\overline {\gamma }}$
; it is
${\overline {\gamma }}$
; it is
 $$ \begin{align} B({\overline{\gamma}}):= \sum_{o \in O} e \cdot \mathrm{min}\{s_i \mid \mathcal{L}_i \in o\}. \end{align} $$
$$ \begin{align} B({\overline{\gamma}}):= \sum_{o \in O} e \cdot \mathrm{min}\{s_i \mid \mathcal{L}_i \in o\}. \end{align} $$
Theorem 2.3 (Bouw)
The integer
![]() $B({\overline {\gamma }})$
is an upper bound for the p-rank of a
$B({\overline {\gamma }})$
is an upper bound for the p-rank of a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover of
$\mathbb {Z}/\ell \mathbb {Z}$
-cover of
![]() ${\mathbb P}^1$
with inertia type
${\mathbb P}^1$
with inertia type
![]() ${\overline {\gamma }}$
[Reference Bouw7, p. 300, (1)]. This upper bound
${\overline {\gamma }}$
[Reference Bouw7, p. 300, (1)]. This upper bound
![]() $B({\overline {\gamma }})$
occurs as the p-rank of a
$B({\overline {\gamma }})$
occurs as the p-rank of a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover of
$\mathbb {Z}/\ell \mathbb {Z}$
-cover of
![]() ${\mathbb P}^1$
with inertia type
${\mathbb P}^1$
with inertia type
![]() ${\overline {\gamma }}$
if
${\overline {\gamma }}$
if
![]() $p \geq \ell (n-3)$
[Reference Bouw7, Th. 6.1], or if
$p \geq \ell (n-3)$
[Reference Bouw7, Th. 6.1], or if
![]() $p = \pm 1 \bmod \ell $
[Reference Bouw7, Props. 7.4 and 7.8], or if
$p = \pm 1 \bmod \ell $
[Reference Bouw7, Props. 7.4 and 7.8], or if
![]() $n=4$
[Reference Bouw7, Prop. 7.7].
$n=4$
[Reference Bouw7, Prop. 7.7].
3 The moduli space of
 $\mathbb {Z}/\ell \mathbb {Z}$
-covers and its boundary
$\mathbb {Z}/\ell \mathbb {Z}$
-covers and its boundary
In this section, we introduce the material needed to study p-ranks of cyclic covers from a moduli-theoretic approach. Recall that
![]() $G=\mathbb {Z}/\ell \mathbb {Z}$
.
$G=\mathbb {Z}/\ell \mathbb {Z}$
.
3.1 Moduli spaces of stable
 $\mathbb {Z}/\ell \mathbb {Z}$
-covers
$\mathbb {Z}/\ell \mathbb {Z}$
-covers
We define moduli functors on the category of schemes over k whose S-points represent the listed objects:
-
1.
 $\overline {{\mathcal T}}_{\ell , g}$
: admissible stable G-curves
$\overline {{\mathcal T}}_{\ell , g}$
: admissible stable G-curves
 $(Y/S, \iota _0)$
with
$(Y/S, \iota _0)$
with
 $Y/S$
of genus g.
$Y/S$
of genus g. -
2.
 ${\widetilde {{\mathcal T}}}_{\ell , g}$
:
${\widetilde {{\mathcal T}}}_{\ell , g}$
:
 $(Y/S, \iota _0)$
as above, together with a labeling
$(Y/S, \iota _0)$
as above, together with a labeling
 $\eta $
of the smooth ramification locus.
$\eta $
of the smooth ramification locus. -
3.
 ${\widetilde {{\mathcal T}}}_{\ell , g; t}$
:
${\widetilde {{\mathcal T}}}_{\ell , g; t}$
:
 $(Y/S, \iota , \eta )$
as above, together with a mark
$(Y/S, \iota , \eta )$
as above, together with a mark
 $R_\Xi $
of degree t such that
$R_\Xi $
of degree t such that
 $(Y/S,R_\Xi )$
is stably marked.
$(Y/S,R_\Xi )$
is stably marked.
Let
![]() ${\mathcal T}_{\ell ,g} \subset \overline {{\mathcal T}}_{\ell , g}$
be the sublocus representing smooth G-curves.
${\mathcal T}_{\ell ,g} \subset \overline {{\mathcal T}}_{\ell , g}$
be the sublocus representing smooth G-curves.
Let
![]() $\gamma : \{1, \ldots , n\} \to (\mathbb {Z}/\ell \mathbb {Z})^*$
be a class vector of length
$\gamma : \{1, \ldots , n\} \to (\mathbb {Z}/\ell \mathbb {Z})^*$
be a class vector of length
![]() $n=n(\gamma )$
. By (1),
$n=n(\gamma )$
. By (1),
![]() $\gamma $
determines the genus
$\gamma $
determines the genus
![]() $g=g(\gamma )=(n-2)(\ell -1)/2$
. Let
$g=g(\gamma )=(n-2)(\ell -1)/2$
. Let
![]() ${\widetilde {{\mathcal T}}}_{\ell , \gamma } \subset {\widetilde {{\mathcal T}}}_{\ell ,g}$
be the substack for which
${\widetilde {{\mathcal T}}}_{\ell , \gamma } \subset {\widetilde {{\mathcal T}}}_{\ell ,g}$
be the substack for which
![]() $(Y/S,\iota _0, \eta )$
has class vector
$(Y/S,\iota _0, \eta )$
has class vector
![]() $\gamma $
. Let
$\gamma $
. Let
![]() ${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}} \subset {\overline {{\mathcal T}}}_{\ell ,g}$
be the substack for which
${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}} \subset {\overline {{\mathcal T}}}_{\ell ,g}$
be the substack for which
![]() $(Y/S,\iota _0)$
has inertia type
$(Y/S,\iota _0)$
has inertia type
![]() ${\overline {\gamma }}$
.
${\overline {\gamma }}$
.
If two class vectors
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
yield the same inertia type, so that
$\gamma '$
yield the same inertia type, so that
![]() ${\overline {\gamma }} = {\overline {\gamma }}'$
, then there is a permutation
${\overline {\gamma }} = {\overline {\gamma }}'$
, then there is a permutation
![]() $\varpi $
of
$\varpi $
of
![]() $\{1, \ldots , n\}$
such that
$\{1, \ldots , n\}$
such that
![]() $\gamma ' = \gamma \circ \varpi $
. This relabeling of the branch locus yields an isomorphism
$\gamma ' = \gamma \circ \varpi $
. This relabeling of the branch locus yields an isomorphism
![]() ${\widetilde {{\mathcal T}}}_{\ell , \gamma } \simeq {\widetilde {{\mathcal T}}}_{\ell , {\gamma \circ \varpi }}$
. Suppose
${\widetilde {{\mathcal T}}}_{\ell , \gamma } \simeq {\widetilde {{\mathcal T}}}_{\ell , {\gamma \circ \varpi }}$
. Suppose
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
differ by an automorphism of G, so that there exists
$\gamma '$
differ by an automorphism of G, so that there exists
![]() $\tau \in \mathrm {Aut}(G)$
such that
$\tau \in \mathrm {Aut}(G)$
such that
![]() $\gamma '= \tau \circ \gamma $
. This relabeling of the G-action yields an isomorphism
$\gamma '= \tau \circ \gamma $
. This relabeling of the G-action yields an isomorphism
![]() ${\widetilde {{\mathcal T}}}_{\ell , \gamma } \simeq {\widetilde {{\mathcal T}}}_{\ell , \tau \circ \gamma }$
.
${\widetilde {{\mathcal T}}}_{\ell , \gamma } \simeq {\widetilde {{\mathcal T}}}_{\ell , \tau \circ \gamma }$
.
Lemma 3.1.
-
1.
 ${\widetilde {{\mathcal T}}}_{\ell ,g}$
and
${\widetilde {{\mathcal T}}}_{\ell ,g}$
and
 ${\overline {{\mathcal T}}}_{\ell , g}$
are smooth, proper Deligne–Mumford stacks over k.
${\overline {{\mathcal T}}}_{\ell , g}$
are smooth, proper Deligne–Mumford stacks over k. -
2.
 ${\mathcal T}_{\ell , g}$
is open and dense in
${\mathcal T}_{\ell , g}$
is open and dense in
 ${\overline {{\mathcal T}}}_{\ell , g}$
.
${\overline {{\mathcal T}}}_{\ell , g}$
. -
3. The forgetful functor
 ${\widetilde {{\mathcal T}}}_{\ell , \gamma } \to {\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
is étale and Galois.
${\widetilde {{\mathcal T}}}_{\ell , \gamma } \to {\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
is étale and Galois. -
4.
 ${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
is an irreducible component of
${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
is an irreducible component of
 ${\overline {{\mathcal T}}}_{\ell , g}$
.
${\overline {{\mathcal T}}}_{\ell , g}$
. -
5. The dimension of
 ${\mathcal T}_{\ell ,{{\overline {\gamma }}} }$
is
${\mathcal T}_{\ell ,{{\overline {\gamma }}} }$
is
 $n-3$
.
$n-3$
.
Proof. See [Reference Achter and Pries3, Lems. 2.2–2.4].
3.2 Clutching maps
We review the clutching maps
![]() $\kappa _{g_1,g_2}$
and
$\kappa _{g_1,g_2}$
and
![]() $\lambda _{g_1,g_2}$
of [Reference Knudsen15]. Each of these is the restriction of a finite, unramified morphism between moduli spaces of labeled curves. They can be described in terms of their images on S-points for an arbitrary k-scheme S. We give explicit descriptions only for sufficiently general S-points and defer to [Reference Knudsen15] for complete definitions. A stable curve Y has compact type if its dual graph is a tree or, equivalently, if
$\lambda _{g_1,g_2}$
of [Reference Knudsen15]. Each of these is the restriction of a finite, unramified morphism between moduli spaces of labeled curves. They can be described in terms of their images on S-points for an arbitrary k-scheme S. We give explicit descriptions only for sufficiently general S-points and defer to [Reference Knudsen15] for complete definitions. A stable curve Y has compact type if its dual graph is a tree or, equivalently, if
![]() $\mathrm {Pic}^0(Y)$
is represented by an abelian scheme.
$\mathrm {Pic}^0(Y)$
is represented by an abelian scheme.
For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\gamma _i$
denote a class vector with length
$\gamma _i$
denote a class vector with length
![]() $n_i=n_i(\gamma _i)$
and let
$n_i=n_i(\gamma _i)$
and let
![]() $g_i=g(\gamma _i)$
.
$g_i=g(\gamma _i)$
.
3.2.1 Clutching maps (compact type)
There is a closed immersion [Reference Knudsen15, Cor. 3.9]
This clutching map glues two curves
![]() $Y_1/S$
and
$Y_1/S$
and
![]() $Y_2/S$
together to form a curve
$Y_2/S$
together to form a curve
![]() $Y/S$
by identifying the last section of
$Y/S$
by identifying the last section of
![]() $Y_1$
and the first section of
$Y_1$
and the first section of
![]() $Y_2$
in an ordinary double point.
$Y_2$
in an ordinary double point.
As seen in [Reference Achter and Pries3, §2.3], the clutching map extends to the moduli space of labeled
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-curves as follows. Let
$\mathbb {Z}/\ell \mathbb {Z}$
-curves as follows. Let
![]() $g=g_1+g_2$
and
$g=g_1+g_2$
and
![]() $n=n_1+n_2-2$
and
$n=n_1+n_2-2$
and
If
![]() $(Y_i/S, \iota _{0,i}, \eta _i)$
is a labeled G-curve with class vector
$(Y_i/S, \iota _{0,i}, \eta _i)$
is a labeled G-curve with class vector
![]() $\gamma _i$
, for
$\gamma _i$
, for
![]() $i=1,2$
, then the clutched curve
$i=1,2$
, then the clutched curve
![]() $Y/S$
has genus g and admits a G-action
$Y/S$
has genus g and admits a G-action
![]() $\iota _0$
and a labeling
$\iota _0$
and a labeling
![]() $\eta $
with class vector
$\eta $
with class vector
![]() $\gamma $
. Moreover,
$\gamma $
. Moreover,
![]() $Y/S$
can be deformed to a smooth G-curve if and only if the G-action is admissible, that is, if and only if
$Y/S$
can be deformed to a smooth G-curve if and only if the G-action is admissible, that is, if and only if
![]() $\gamma _1(n_1)$
and
$\gamma _1(n_1)$
and
![]() $\gamma _2(1)$
are inverses [Reference Ekedahl8, Prop. 2.2]. In this situation, we write
$\gamma _2(1)$
are inverses [Reference Ekedahl8, Prop. 2.2]. In this situation, we write
By [Reference Bosch, Lütkebohmert and Raynaud6, Ex. 9.2.8],
![]() ${\mathop{\mathrm{Pic}}}^0(Y) \simeq {\mathop{\mathrm{Pic}}}^0(Y_1) \times {\mathop{\mathrm{Pic}}}^0(Y_2)$
. In particular, the p-rank of Y is
${\mathop{\mathrm{Pic}}}^0(Y) \simeq {\mathop{\mathrm{Pic}}}^0(Y_1) \times {\mathop{\mathrm{Pic}}}^0(Y_2)$
. In particular, the p-rank of Y is
The signature type of
![]() $(Y/S, \iota _0)$
is the sum of those for
$(Y/S, \iota _0)$
is the sum of those for
![]() $(Y_i/S, \iota _{0,i})$
.
$(Y_i/S, \iota _{0,i})$
.
For
![]() $1 \leq g_1 \leq g-1$
, let
$1 \leq g_1 \leq g-1$
, let
![]() $\Delta _{g_1}[{\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}]$
be the image of
$\Delta _{g_1}[{\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}]$
be the image of
![]() $\kappa _{g_1,g_2}$
in
$\kappa _{g_1,g_2}$
in
![]() ${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
, where
${\overline {{\mathcal T}}}_{\ell , {\overline {\gamma }}}$
, where
![]() $g_2=g-g_1$
and
$g_2=g-g_1$
and
![]() $(\gamma _1, \gamma _2)$
ranges over the appropriate admissible pairs of class vectors.
$(\gamma _1, \gamma _2)$
ranges over the appropriate admissible pairs of class vectors.
3.2.2 Clutching maps (non-compact type)
In this case, let
![]() $g=g_1+g_2 + (\ell -1)$
and
$g=g_1+g_2 + (\ell -1)$
and
![]() $n=n_1+n_2$
and
$n=n_1+n_2$
and
![]() $\gamma = (\gamma _1(1), \ldots , \gamma _1(n_1), \gamma _2(1), \ldots , \gamma _2(n_2))$
. The other clutching maps are
$\gamma = (\gamma _1(1), \ldots , \gamma _1(n_1), \gamma _2(1), \ldots , \gamma _2(n_2))$
. The other clutching maps are
To define
![]() $\lambda _{g_1,g_2}$
, consider a
$\lambda _{g_1,g_2}$
, consider a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-curve
$\mathbb {Z}/\ell \mathbb {Z}$
-curve
![]() $(Y_i/S, \iota _{0,i})$
with a mark
$(Y_i/S, \iota _{0,i})$
with a mark
![]() $P_i$
, for
$P_i$
, for
![]() $i=1,2$
. One can glue these curves together to form a curve
$i=1,2$
. One can glue these curves together to form a curve
![]() $Y/S$
by identifying the orbits of
$Y/S$
by identifying the orbits of
![]() $P_1$
and
$P_1$
and
![]() $P_2$
in
$P_2$
in
![]() $\ell $
ordinary double points. (Specifically, identify
$\ell $
ordinary double points. (Specifically, identify
![]() $\iota _{0,1}(g)(P_1)$
and
$\iota _{0,1}(g)(P_1)$
and
![]() $\iota _{0,2}(g)(P_2)$
for
$\iota _{0,2}(g)(P_2)$
for
![]() $g \in G$
.) Then
$g \in G$
.) Then
![]() $Y/S$
admits a G-action
$Y/S$
admits a G-action
![]() $\iota _0$
and has inertia type
$\iota _0$
and has inertia type
![]() ${\overline {\gamma }}$
.
${\overline {\gamma }}$
.
Since
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
intersect in more than one point, the curve
$Y_2$
intersect in more than one point, the curve
![]() $Y/S$
has non-compact type. By [Reference Bosch, Lütkebohmert and Raynaud6, Ex. 9.2.8],
$Y/S$
has non-compact type. By [Reference Bosch, Lütkebohmert and Raynaud6, Ex. 9.2.8],
![]() ${\mathop{\mathrm{Pic}}}^0(Y)$
is an extension
${\mathop{\mathrm{Pic}}}^0(Y)$
is an extension
where Z is an
![]() $(\ell -1)$
-dimensional torus. Thus, Y has genus g and the p-rank of Y is
$(\ell -1)$
-dimensional torus. Thus, Y has genus g and the p-rank of Y is
There is an action of
![]() $\mathbb {Z}/\ell \mathbb {Z}$
on Z, and each of the nontrivial eigenspaces has dimension
$\mathbb {Z}/\ell \mathbb {Z}$
on Z, and each of the nontrivial eigenspaces has dimension
![]() $1$
; we define the signature type of Z to be
$1$
; we define the signature type of Z to be
![]() $(1, \ldots , 1)$
. The signature type of
$(1, \ldots , 1)$
. The signature type of
![]() $(Y/S, \iota )$
is the sum of those for
$(Y/S, \iota )$
is the sum of those for
![]() $(Y_i/S, \iota _{0,i})$
and Z.
$(Y_i/S, \iota _{0,i})$
and Z.
For
![]() $0 \leq g_1 \leq g-(\ell -1)$
, let
$0 \leq g_1 \leq g-(\ell -1)$
, let
![]() $\Xi _{g_1}[{\overline {{\mathcal T}}}_{\ell , g}] \subset {\overline {{\mathcal T}}}_{\ell , g}$
be the image of
$\Xi _{g_1}[{\overline {{\mathcal T}}}_{\ell , g}] \subset {\overline {{\mathcal T}}}_{\ell , g}$
be the image of
![]() $\lambda _{g_1,g_2}$
, where
$\lambda _{g_1,g_2}$
, where
![]() $g_2=g-g_1-(\ell -1)$
and
$g_2=g-g_1-(\ell -1)$
and
![]() $(\gamma _1, \gamma _2)$
ranges over the appropriate pairs of class vectors. Let
$(\gamma _1, \gamma _2)$
ranges over the appropriate pairs of class vectors. Let
![]() $\Delta _0[{\overline {{\mathcal T}}}_{\ell , g}]$
be the union of
$\Delta _0[{\overline {{\mathcal T}}}_{\ell , g}]$
be the union of
![]() $\Xi _{g_1}[{\overline {{\mathcal T}}}_{\ell , g}]$
for
$\Xi _{g_1}[{\overline {{\mathcal T}}}_{\ell , g}]$
for
![]() $0 \leq g_1 \leq g-(\ell -1)$
. Then
$0 \leq g_1 \leq g-(\ell -1)$
. Then
![]() $\Delta _0[{\overline {{\mathcal T}}}_{\ell , g}]$
is the set of moduli points of stable
$\Delta _0[{\overline {{\mathcal T}}}_{\ell , g}]$
is the set of moduli points of stable
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-curves of genus g which are not of compact type.
$\mathbb {Z}/\ell \mathbb {Z}$
-curves of genus g which are not of compact type.
3.3 Components and dimension of the boundary
The boundary of
![]() ${\overline {{\mathcal T}}}_{\ell , g}$
is
${\overline {{\mathcal T}}}_{\ell , g}$
is
![]() $\delta {\mathcal T}_{\ell , g} = {\overline {{\mathcal T}}}_{\ell , g} - {\mathcal T}_{\ell , g}$
. If
$\delta {\mathcal T}_{\ell , g} = {\overline {{\mathcal T}}}_{\ell , g} - {\mathcal T}_{\ell , g}$
. If
![]() $g \geq 2$
, then
$g \geq 2$
, then
![]() $\delta {\mathcal T}_{\ell , g}$
is the union of
$\delta {\mathcal T}_{\ell , g}$
is the union of
![]() $\Delta _i = \Delta _{i}[{\overline {{\mathcal T}}}_{\ell , g}]$
for
$\Delta _i = \Delta _{i}[{\overline {{\mathcal T}}}_{\ell , g}]$
for
![]() $1 \leq i \leq g-1$
and
$1 \leq i \leq g-1$
and
![]() $\Xi _i = \Xi _i[{\overline {{\mathcal T}}}_{\ell , g}]$
for
$\Xi _i = \Xi _i[{\overline {{\mathcal T}}}_{\ell , g}]$
for
![]() $0 \leq i \leq g-(\ell -1)$
, some of which may be empty. Note that
$0 \leq i \leq g-(\ell -1)$
, some of which may be empty. Note that
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Delta _{g-i}$
(resp.
$\Delta _{g-i}$
(resp.
![]() $\Xi _i$
and
$\Xi _i$
and
![]() $\Xi _{g-i-(\ell -1)}$
) are the same substack of
$\Xi _{g-i-(\ell -1)}$
) are the same substack of
![]() ${\overline {{\mathcal T}}}_{\ell , g}$
.
${\overline {{\mathcal T}}}_{\ell , g}$
.
If
![]() ${\mathcal S}$
is a stack with a map
${\mathcal S}$
is a stack with a map
![]() ${\mathcal S} \to {\overline {{\mathcal T}}}_{\ell , g}$
, let
${\mathcal S} \to {\overline {{\mathcal T}}}_{\ell , g}$
, let
![]() $\Delta _i[{\mathcal S}]={\mathcal S} \times _{{\overline {{\mathcal T}}}_{\ell , g}} \Delta _i[{\overline {{\mathcal T}}}_{\ell ,g}]$
. So,
$\Delta _i[{\mathcal S}]={\mathcal S} \times _{{\overline {{\mathcal T}}}_{\ell , g}} \Delta _i[{\overline {{\mathcal T}}}_{\ell ,g}]$
. So,
![]() $\Delta _i[{\widetilde {{\mathcal T}}}_{\ell , g}] = {\widetilde {{\mathcal T}}}_{\ell , g}\times _{{\overline {{\mathcal T}}}_{\ell , g}} \Delta _i$
. Similar notation is used for
$\Delta _i[{\widetilde {{\mathcal T}}}_{\ell , g}] = {\widetilde {{\mathcal T}}}_{\ell , g}\times _{{\overline {{\mathcal T}}}_{\ell , g}} \Delta _i$
. Similar notation is used for
![]() $\Xi _i$
.
$\Xi _i$
.
Lemma 3.2. Every irreducible component of
![]() ${\partial }{\overline {{\mathcal T}}}_{\ell , g}$
has dimension
${\partial }{\overline {{\mathcal T}}}_{\ell , g}$
has dimension
![]() $\mathrm {dim}({\mathcal T}_{\ell , g})-1$
.
$\mathrm {dim}({\mathcal T}_{\ell , g})-1$
.
Proof. Let W be an irreducible component of
![]() $\delta {\mathcal T}_{\ell , g}$
. There is an inertia type
$\delta {\mathcal T}_{\ell , g}$
. There is an inertia type
![]() ${\overline {\gamma }}$
such that W is either a component of (i)
${\overline {\gamma }}$
such that W is either a component of (i)
![]() $\Delta _i[{\mathcal T}_{\ell , {\overline {\gamma }}}]$
for some
$\Delta _i[{\mathcal T}_{\ell , {\overline {\gamma }}}]$
for some
![]() $0 \leq i \leq g-1$
or (ii)
$0 \leq i \leq g-1$
or (ii)
![]() $\Xi _i[{\mathcal T}_{\ell , {\overline {\gamma }}}]$
for some
$\Xi _i[{\mathcal T}_{\ell , {\overline {\gamma }}}]$
for some
![]() $0 \leq i \leq g-(\ell -1)$
. By Lemma 3.1(5), it suffices to show that
$0 \leq i \leq g-(\ell -1)$
. By Lemma 3.1(5), it suffices to show that
![]() $\mathrm {dim}(W)=n-4$
.
$\mathrm {dim}(W)=n-4$
.
Case (i): In this case, a generic point of W is the moduli point of a singular curve Y with two irreducible components
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
intersecting in one ordinary double point y. Let
$Y_2$
intersecting in one ordinary double point y. Let
![]() ${\overline {\gamma }}_i$
be the inertia type of the restriction of the
${\overline {\gamma }}_i$
be the inertia type of the restriction of the
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-action to
$\mathbb {Z}/\ell \mathbb {Z}$
-action to
![]() $Y_i$
, and let
$Y_i$
, and let
![]() $n_i=n({\overline {\gamma }}_i)$
. Then
$n_i=n({\overline {\gamma }}_i)$
. Then
![]() $n_1+n_2 -2 = n$
since y is a ramification point for the two restrictions. So
$n_1+n_2 -2 = n$
since y is a ramification point for the two restrictions. So
Case (ii): In this case, a generic point of W is the moduli point of a singular curve Y with two irreducible components
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
, of genera i and
$Y_2$
, of genera i and
![]() $g-i-(\ell -1)$
intersecting at one unramified
$g-i-(\ell -1)$
intersecting at one unramified
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-orbit. Let
$\mathbb {Z}/\ell \mathbb {Z}$
-orbit. Let
![]() ${\overline {\gamma }}_i$
be the inertia type of the restriction of the
${\overline {\gamma }}_i$
be the inertia type of the restriction of the
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-action to
$\mathbb {Z}/\ell \mathbb {Z}$
-action to
![]() $Y_i$
, and let
$Y_i$
, and let
![]() $n_i=n({\overline {\gamma }}_i)$
. Then
$n_i=n({\overline {\gamma }}_i)$
. Then
![]() $n_1+n_2=n$
. There is a one-dimensional choice of an unramified orbit on each of
$n_1+n_2=n$
. There is a one-dimensional choice of an unramified orbit on each of
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
. So,
$Y_2$
. So,
The next result is used to find an upper bound on the dimension of the p-rank strata.
Proposition 3.3. If
![]() ${\mathcal S} \subset {\overline {{\mathcal T}}}_{\ell ,g}$
has the property that
${\mathcal S} \subset {\overline {{\mathcal T}}}_{\ell ,g}$
has the property that
![]() ${\mathcal S}$
intersects
${\mathcal S}$
intersects
![]() $\Delta _i$
, then
$\Delta _i$
, then
Proof. A smooth proper stack has the same intersection-theoretic properties as a smooth proper scheme [Reference Vistoli23, p. 614]. In particular, if two closed substacks of
![]() ${\overline {{\mathcal T}}}_g$
intersect, then the codimension of their intersection is at most the sum of their codimensions. Now,
${\overline {{\mathcal T}}}_g$
intersect, then the codimension of their intersection is at most the sum of their codimensions. Now,
![]() $\Delta _i[{\overline {{\mathcal T}}}_{\ell ,g}]$
is a closed substack of
$\Delta _i[{\overline {{\mathcal T}}}_{\ell ,g}]$
is a closed substack of
![]() ${\overline {{\mathcal T}}}_{\ell ,g}$
. It suffices to consider the case that
${\overline {{\mathcal T}}}_{\ell ,g}$
. It suffices to consider the case that
![]() ${\mathcal S}$
is closed. Thus,
${\mathcal S}$
is closed. Thus,
The result follows from Lemma 3.2 since
![]() $\mathrm {codim}(\Delta _i, {\overline {{\mathcal T}}}_{\ell , g})=1$
.
$\mathrm {codim}(\Delta _i, {\overline {{\mathcal T}}}_{\ell , g})=1$
.
3.4 The p-rank stratification
If A is a semi-abelian scheme over a Deligne–Mumford stack
![]() ${\mathcal S}$
, then there is a stratification
${\mathcal S}$
, then there is a stratification
![]() ${\mathcal S} = \cup {\mathcal S}^{f}$
by locally closed reduced substacks such that
${\mathcal S} = \cup {\mathcal S}^{f}$
by locally closed reduced substacks such that
![]() $s \in {\mathcal S}^f(k)$
if and only if
$s \in {\mathcal S}^f(k)$
if and only if
![]() $f(A_s) =f$
[Reference Katz14, Th. 2.3.1] (see also [Reference Achter and Pries4, Lem. 2.1]). For example,
$f(A_s) =f$
[Reference Katz14, Th. 2.3.1] (see also [Reference Achter and Pries4, Lem. 2.1]). For example,
![]() ${{\mathcal T}}_{\ell , g}^f$
is the locally closed reduced substack of
${{\mathcal T}}_{\ell , g}^f$
is the locally closed reduced substack of
![]() ${{\mathcal T}}_{\ell ,g}$
whose points represent smooth
${{\mathcal T}}_{\ell ,g}$
whose points represent smooth
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-curves of genus g with p-rank f.
$\mathbb {Z}/\ell \mathbb {Z}$
-curves of genus g with p-rank f.
We use the following notation for the p-rank f stratum of the boundary:
![]() $\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}]^f:=(\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}])^f$
. These strata are easy to describe using the clutching maps. First, if
$\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}]^f:=(\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}])^f$
. These strata are easy to describe using the clutching maps. First, if
![]() $1 \leq i \leq g-1$
, then (3) implies that
$1 \leq i \leq g-1$
, then (3) implies that
![]() $\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}]^f$
is the union of the images of
$\Delta _i[{\overline {{\mathcal T}}}_{\ell , g}]^f$
is the union of the images of
![]() ${\widetilde {{\mathcal T}}}_{\ell , i}^{f_1} \times {\widetilde {{\mathcal T}}}_{\ell , g-i}^{f_2}$
under
${\widetilde {{\mathcal T}}}_{\ell , i}^{f_1} \times {\widetilde {{\mathcal T}}}_{\ell , g-i}^{f_2}$
under
![]() $\kappa _{i, g-i}$
as
$\kappa _{i, g-i}$
as
![]() $(f_1,f_2)$
ranges over all pairs (satisfying Lemma 2.2) such that
$(f_1,f_2)$
ranges over all pairs (satisfying Lemma 2.2) such that
Second, if
![]() $f \geq 2$
and
$f \geq 2$
and
![]() $0 \leq i \leq g-(\ell -1)$
, then (4) implies that
$0 \leq i \leq g-(\ell -1)$
, then (4) implies that
![]() $\Xi _i[{\overline {{\mathcal T}}}_{\ell , g}]^f$
is the union of the images of
$\Xi _i[{\overline {{\mathcal T}}}_{\ell , g}]^f$
is the union of the images of
![]() ${\overline {{\mathcal T}}}_{\ell , i;1}^{f_1} \times {\overline {{\mathcal T}}}_{\ell , g-(\ell -1)-i;1}^{f_2}$
under
${\overline {{\mathcal T}}}_{\ell , i;1}^{f_1} \times {\overline {{\mathcal T}}}_{\ell , g-(\ell -1)-i;1}^{f_2}$
under
![]() $\lambda _{i, g-(\ell -1)-i}$
as
$\lambda _{i, g-(\ell -1)-i}$
as
![]() $(f_1,f_2)$
ranges over all pairs (satisfying Lemma 2.2) such that
$(f_1,f_2)$
ranges over all pairs (satisfying Lemma 2.2) such that
3.5 Shimura varieties
We briefly review some notation about Shimura varieties that we need in §§5.3 and 6.2. We refer to [Reference Li, Mantovan, Pries and Tang17, §3.3] for a longer explanation.
Notation 3.4. Let
![]() $\ell $
be an odd prime. Consider an inertia type
$\ell $
be an odd prime. Consider an inertia type
![]() ${\overline {\gamma }}$
for
${\overline {\gamma }}$
for
![]() $\ell $
. It determines the number of branch points
$\ell $
. It determines the number of branch points
![]() $n=n({\overline {\gamma }})$
and the genus
$n=n({\overline {\gamma }})$
and the genus
![]() $g=g({\overline {\gamma }})$
as in (1) for a
$g=g({\overline {\gamma }})$
as in (1) for a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover
$\mathbb {Z}/\ell \mathbb {Z}$
-cover
![]() $Y \to {\mathbb P}^1$
with inertia type
$Y \to {\mathbb P}^1$
with inertia type
![]() ${\overline {\gamma }}$
. Furthermore, it determines the signature type of the cover as in Lemma 2.1.
${\overline {\gamma }}$
. Furthermore, it determines the signature type of the cover as in Lemma 2.1.
Recall that
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
is the moduli space of
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
is the moduli space of
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-covers
$\mathbb {Z}/\ell \mathbb {Z}$
-covers
![]() $Y \to {\mathbb P}^1$
with inertia type
$Y \to {\mathbb P}^1$
with inertia type
![]() ${\overline {\gamma }}$
. By Lemma 3.1,
${\overline {\gamma }}$
. By Lemma 3.1,
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
is irreducible and has dimension
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
is irreducible and has dimension
![]() $n({\overline {\gamma }})-3$
.
$n({\overline {\gamma }})-3$
.
Notation 3.5. Let
![]() ${\mathcal A}_g$
be the moduli space of principally polarized abelian varieties of dimension g. Consider the image of
${\mathcal A}_g$
be the moduli space of principally polarized abelian varieties of dimension g. Consider the image of
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
in
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
in
![]() ${\mathcal A}_g$
. Let
${\mathcal A}_g$
. Let
![]() $Z_{{\overline {\gamma }}}=Z(\ell , n, {\overline {\gamma }})$
be the closure of this image; its points represent Jacobians of curves (smooth or of compact type) that admit a
$Z_{{\overline {\gamma }}}=Z(\ell , n, {\overline {\gamma }})$
be the closure of this image; its points represent Jacobians of curves (smooth or of compact type) that admit a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover of
$\mathbb {Z}/\ell \mathbb {Z}$
-cover of
![]() ${\mathbb P}^1$
with inertia type
${\mathbb P}^1$
with inertia type
![]() ${\overline {\gamma }}$
.
${\overline {\gamma }}$
.
Attached to the data of
![]() $\ell $
and the signature type, there is a PEL-type Shimura variety
$\ell $
and the signature type, there is a PEL-type Shimura variety
![]() $\mathrm {Sh}$
. Let
$\mathrm {Sh}$
. Let
![]() $\Sigma _{{\overline {\gamma }}}=\Sigma (\ell , n, {\overline {\gamma }})$
be the irreducible component of
$\Sigma _{{\overline {\gamma }}}=\Sigma (\ell , n, {\overline {\gamma }})$
be the irreducible component of
![]() $\mathrm {Sh}$
that contains
$\mathrm {Sh}$
that contains
![]() $Z_{{\overline {\gamma }}}$
.
$Z_{{\overline {\gamma }}}$
.
4 Intersection of the p-rank
 $0$
stratum with the boundary
$0$
stratum with the boundary
In this section, we study the geometry of the p-rank stratification on the moduli space of cyclic degree
![]() $\ell $
covers of the projective line.
$\ell $
covers of the projective line.
Recall that p is a prime such that
![]() $p \not = \ell $
and e is the order of p modulo
$p \not = \ell $
and e is the order of p modulo
![]() $\ell $
. The formula for the upper bound
$\ell $
. The formula for the upper bound
![]() $B({\overline {\gamma }})$
for the p-rank of a cover with inertia type
$B({\overline {\gamma }})$
for the p-rank of a cover with inertia type
![]() ${\overline {\gamma }}$
is in (2). Let f be a multiple of e such that
${\overline {\gamma }}$
is in (2). Let f be a multiple of e such that
![]() $0 \leq f < B({\overline {\gamma }})$
. Define
$0 \leq f < B({\overline {\gamma }})$
. Define
![]() $\epsilon = 1$
if
$\epsilon = 1$
if
![]() $p \equiv 1 \bmod \ell $
and
$p \equiv 1 \bmod \ell $
and
![]() $\epsilon =0$
otherwise.
$\epsilon =0$
otherwise.
We first give a lower bound on the dimension of the p-rank strata.
Proposition 4.1. Suppose the p-rank f stratum
![]() ${\overline {{\mathcal T}}}^f_{\ell ,{\overline {\gamma }}}$
is non-empty, and let
${\overline {{\mathcal T}}}^f_{\ell ,{\overline {\gamma }}}$
is non-empty, and let
![]() ${\mathcal S}$
be an irreducible component of it. Then
${\mathcal S}$
be an irreducible component of it. Then
Proof. The p-ranks which occur on
![]() ${\overline {{\mathcal T}}}_{\ell ,{\overline {\gamma }}}$
are multiples of e by Lemma 2.2 and are at most
${\overline {{\mathcal T}}}_{\ell ,{\overline {\gamma }}}$
are multiples of e by Lemma 2.2 and are at most
![]() $B({\overline {\gamma }})$
by Theorem 2.3. Furthermore, if
$B({\overline {\gamma }})$
by Theorem 2.3. Furthermore, if
![]() $p \equiv 1 \bmod \ell $
, then
$p \equiv 1 \bmod \ell $
, then
![]() $e=1$
and
$e=1$
and
![]() $f \not = g-1 = B({\overline {\gamma }}) -1$
by Lemma 2.2. So the number of integers
$f \not = g-1 = B({\overline {\gamma }}) -1$
by Lemma 2.2. So the number of integers
![]() $f'$
such that
$f'$
such that
![]() $f < f' \leq B({\overline {\gamma }})$
which can occur as the p-ranks for points of
$f < f' \leq B({\overline {\gamma }})$
which can occur as the p-ranks for points of
![]() ${\overline {{\mathcal T}}}_{\ell ,{\overline {\gamma }}}$
is at most
${\overline {{\mathcal T}}}_{\ell ,{\overline {\gamma }}}$
is at most
![]() $(B({\overline {\gamma }})-f)/e + \epsilon $
. The statement is then an immediate application of the purity result of Oort [Reference Oort20, Lem. 1.6] which states that if the p-rank changes, then it does so on a subspace of codimension
$(B({\overline {\gamma }})-f)/e + \epsilon $
. The statement is then an immediate application of the purity result of Oort [Reference Oort20, Lem. 1.6] which states that if the p-rank changes, then it does so on a subspace of codimension
![]() $1$
.
$1$
.
Remark 4.2. For
![]() $\ell \geq 5$
, the lower bound on the right-hand side of (5) is positive only when f is large relative to g. For example, if
$\ell \geq 5$
, the lower bound on the right-hand side of (5) is positive only when f is large relative to g. For example, if
![]() $\ell =5$
and
$\ell =5$
and
![]() $p \equiv 1 \bmod 5$
, then it is
$p \equiv 1 \bmod 5$
, then it is
![]() $-g/2 + f$
.
$-g/2 + f$
.
In the next result, assuming that the p-rank
![]() $0$
stratum
$0$
stratum
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
is non-empty, we show that it intersects the boundary deeply (in the sense that the intersection contains points corresponding to reducible curves with many components).
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
is non-empty, we show that it intersects the boundary deeply (in the sense that the intersection contains points corresponding to reducible curves with many components).
Theorem 4.3. Suppose
![]() ${\mathcal S}$
is an irreducible component of the p-rank
${\mathcal S}$
is an irreducible component of the p-rank
![]() $0$
stratum
$0$
stratum
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
of
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
of
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
. Let
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
. Let
![]() $\sigma = \mathrm {dim}({\mathcal S})$
. Then there exists
$\sigma = \mathrm {dim}({\mathcal S})$
. Then there exists
![]() $\eta \in {\mathcal S}$
such that the curve
$\eta \in {\mathcal S}$
such that the curve
![]() $Y_\eta $
of compact type represented by
$Y_\eta $
of compact type represented by
![]() $\eta $
is reducible, with at least
$\eta $
is reducible, with at least
![]() $\sigma + 1$
components, such that the
$\sigma + 1$
components, such that the
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-action stabilizes and acts nontrivially on each component.
$\mathbb {Z}/\ell \mathbb {Z}$
-action stabilizes and acts nontrivially on each component.
Before proving this theorem, we explain its significance.
Remark 4.4.
-
1. Recall that
 $\sigma \geq \mathrm {dim}({\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}} }) - B({\overline {\gamma }})/e + \epsilon $
by Proposition 4.1. So, for each irreducible component of the p-rank
$\sigma \geq \mathrm {dim}({\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}} }) - B({\overline {\gamma }})/e + \epsilon $
by Proposition 4.1. So, for each irreducible component of the p-rank
 $0$
stratum, Theorem 4.3 guarantees the existence of a point representing a curve that is reducible, with many components. The existence of a degenerate point of this type can be helpful for studying the p-rank
$0$
stratum, Theorem 4.3 guarantees the existence of a point representing a curve that is reducible, with many components. The existence of a degenerate point of this type can be helpful for studying the p-rank
 $0$
strata. We illustrate this with several applications in §6.2.
$0$
strata. We illustrate this with several applications in §6.2. -
2. Theorem 4.3 is a generalization of [Reference Achter and Pries5, Th. 3.11(c)], which is the case
 $\ell =2$
. Suppose
$\ell =2$
. Suppose
 $\ell =2$
and
$\ell =2$
and
 $g \geq 2$
, in which case there is a unique inertia type
$g \geq 2$
, in which case there is a unique inertia type
 ${\overline {\gamma }}$
for hyperelliptic curves of genus g. In this case, Theorem 4.3 applies to an irreducible component
${\overline {\gamma }}$
for hyperelliptic curves of genus g. In this case, Theorem 4.3 applies to an irreducible component
 ${\mathcal S}$
of the p-rank
${\mathcal S}$
of the p-rank
 $0$
stratum of the locus of hyperelliptic curves of genus g. By [Reference Glass and Pries11, Prop. 2],
$0$
stratum of the locus of hyperelliptic curves of genus g. By [Reference Glass and Pries11, Prop. 2],
 $\sigma = \mathrm {dim}({\mathcal S}) = g-1$
. So Theorem 4.3 shows that
$\sigma = \mathrm {dim}({\mathcal S}) = g-1$
. So Theorem 4.3 shows that
 ${\mathcal S}$
contains a point representing a curve that has g components (each of which has genus
${\mathcal S}$
contains a point representing a curve that has g components (each of which has genus
 $1$
and is thus a supersingular elliptic curve); this is the conclusion of [Reference Achter and Pries5, Th. 3.11(c)].
$1$
and is thus a supersingular elliptic curve); this is the conclusion of [Reference Achter and Pries5, Th. 3.11(c)]. -
3. In contrast, when
 $\ell $
is odd, then usually
$\ell $
is odd, then usually
 $\sigma < g-1$
. Thus, Theorem 4.3 does not imply that
$\sigma < g-1$
. Thus, Theorem 4.3 does not imply that
 ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
contains a point representing a reducible curve with g components. This makes it harder to study the case when
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
contains a point representing a reducible curve with g components. This makes it harder to study the case when
 $\ell $
is odd.
$\ell $
is odd. -
4. It is not possible to prove Theorem 4.3 using results on the boundary of the moduli space of n-marked curves of genus
 $0$
. The reason is that the relationship between the p-rank and the location of the branch points is extremely complicated. As an example of this, see the case that
$0$
. The reason is that the relationship between the p-rank and the location of the branch points is extremely complicated. As an example of this, see the case that
 $\ell =3$
and
$\ell =3$
and
 $g=2$
studied in Lemma 7.1. In other words, it is not clear how to maintain the p-rank
$g=2$
studied in Lemma 7.1. In other words, it is not clear how to maintain the p-rank
 $0$
condition when deforming the curve by moving the branch points.
$0$
condition when deforming the curve by moving the branch points.
Proof.
(Proof of Theorem 4.3). The proof is by induction on the number of branch points
![]() $n=n({\overline {\gamma }})$
. This is equivalent to induction on the genus
$n=n({\overline {\gamma }})$
. This is equivalent to induction on the genus
![]() $g=g({\overline {\gamma }})$
, because
$g=g({\overline {\gamma }})$
, because
![]() $g=(n-2)(\ell -1)/2$
. For the base case, when
$g=(n-2)(\ell -1)/2$
. For the base case, when
![]() $n=3$
and
$n=3$
and
![]() $g=(\ell -1)/2$
, the statement is vacuous since
$g=(\ell -1)/2$
, the statement is vacuous since
![]() ${\mathcal T}_{\ell , {{\overline {\gamma }}} }$
has dimension
${\mathcal T}_{\ell , {{\overline {\gamma }}} }$
has dimension
![]() $0$
.
$0$
.
Suppose that the statement is true for all inertia types
![]() ${\overline {\gamma }}'$
for which the genus
${\overline {\gamma }}'$
for which the genus
![]() $g'$
is less than g. Let
$g'$
is less than g. Let
![]() ${\overline {\gamma }}$
be an inertia type for which the genus is g, and let
${\overline {\gamma }}$
be an inertia type for which the genus is g, and let
![]() ${\mathcal S}$
be an irreducible component of
${\mathcal S}$
be an irreducible component of
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
. When
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
. When
![]() $\sigma =0$
, the statement is vacuous.
$\sigma =0$
, the statement is vacuous.
Suppose
![]() $\sigma> 0$
. Since
$\sigma> 0$
. Since
![]() ${\mathcal T}_{\ell , {{\overline {\gamma }}}}$
is affine,
${\mathcal T}_{\ell , {{\overline {\gamma }}}}$
is affine,
![]() ${\mathcal S}$
intersects a boundary component of
${\mathcal S}$
intersects a boundary component of
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
. The points of
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}$
. The points of
![]() ${\mathcal S}$
represent curves whose p-rank is
${\mathcal S}$
represent curves whose p-rank is
![]() $0$
, and hence (4) implies that
$0$
, and hence (4) implies that
![]() ${\mathcal S}$
does not intersect
${\mathcal S}$
does not intersect
![]() $\Delta _{0}$
. Thus,
$\Delta _{0}$
. Thus,
![]() ${\mathcal S}$
intersects
${\mathcal S}$
intersects
![]() $\Delta _j$
for some
$\Delta _j$
for some
![]() $1 \leq j \leq g-1$
. A point of
$1 \leq j \leq g-1$
. A point of
![]() $\Delta _j[{\mathcal S}]$
represents a curve having at least two components (which completes the proof when
$\Delta _j[{\mathcal S}]$
represents a curve having at least two components (which completes the proof when
![]() $\sigma =1$
).
$\sigma =1$
).
By Proposition 3.3,
![]() $\mathrm {dim}(\Delta _j[{\mathcal S}]) \geq \sigma -1$
. A point
$\mathrm {dim}(\Delta _j[{\mathcal S}]) \geq \sigma -1$
. A point
![]() $\eta _0$
of
$\eta _0$
of
![]() $\Delta _j[{\mathcal S}]$
is in the image of a clutching morphism. Specifically, there is an admissible pair of inertia types
$\Delta _j[{\mathcal S}]$
is in the image of a clutching morphism. Specifically, there is an admissible pair of inertia types
![]() ${{\overline {\gamma }}} _1, {{\overline {\gamma }}} _2$
, and points
${{\overline {\gamma }}} _1, {{\overline {\gamma }}} _2$
, and points
![]() $\xi _i \in \tilde {{\mathcal T}}_{\ell , {{\overline {\gamma }}} _i}$
, for
$\xi _i \in \tilde {{\mathcal T}}_{\ell , {{\overline {\gamma }}} _i}$
, for
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() $\eta _0=\kappa _{j, g-j}(\xi _1, \xi _2)$
. Since
$\eta _0=\kappa _{j, g-j}(\xi _1, \xi _2)$
. Since
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
, there is an irreducible component
${\overline {{\mathcal T}}}_{\ell , {{\overline {\gamma }}}}^0$
, there is an irreducible component
![]() $\Gamma _i$
of
$\Gamma _i$
of
![]() $\tilde {{\mathcal T}}_{\ell , {{\overline {\gamma }}}_i}$
, for
$\tilde {{\mathcal T}}_{\ell , {{\overline {\gamma }}}_i}$
, for
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() $\kappa _{j, g-j}(\Gamma _1, \Gamma _2) \subset \Delta _j[{\mathcal S}]$
.
$\kappa _{j, g-j}(\Gamma _1, \Gamma _2) \subset \Delta _j[{\mathcal S}]$
.
Note that
![]() $g({{\overline {\gamma }}} _i) <g$
. Let
$g({{\overline {\gamma }}} _i) <g$
. Let
![]() $\sigma _i=\mathrm {dim}(\Gamma _i)$
. Then
$\sigma _i=\mathrm {dim}(\Gamma _i)$
. Then
![]() $\sigma _1+\sigma _2 \geq \sigma -1$
. By the inductive hypothesis, for
$\sigma _1+\sigma _2 \geq \sigma -1$
. By the inductive hypothesis, for
![]() $i=1,2$
, there exists
$i=1,2$
, there exists
![]() $\eta _i \in \Gamma _i$
such that the curve
$\eta _i \in \Gamma _i$
such that the curve
![]() $Y_{\eta _i}$
of compact type represented by
$Y_{\eta _i}$
of compact type represented by
![]() $\eta _i$
has at least
$\eta _i$
has at least
![]() $\sigma _i+1$
components. Then
$\sigma _i+1$
components. Then
![]() $\kappa _{j, g-j}(\eta _1, \eta _2) \in \Delta _j[{\mathcal S}]$
has at least
$\kappa _{j, g-j}(\eta _1, \eta _2) \in \Delta _j[{\mathcal S}]$
has at least
![]() $(\sigma _1+1)+(\sigma _2+1) \geq \sigma +1$
components.
$(\sigma _1+1)+(\sigma _2+1) \geq \sigma +1$
components.
5 Trielliptic covers
In this section, we specialize to the case
![]() $\ell = 3$
. Suppose
$\ell = 3$
. Suppose
![]() $p \not = 3$
is prime. We study the p-ranks of trielliptic curves, which are
$p \not = 3$
is prime. We study the p-ranks of trielliptic curves, which are
![]() $\mathbb {Z}/3 \mathbb {Z}$
-covers of
$\mathbb {Z}/3 \mathbb {Z}$
-covers of
![]() ${\mathbb P}^1$
. Suppose
${\mathbb P}^1$
. Suppose
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $(r,s)$
is a signature type for g.
$(r,s)$
is a signature type for g.
In Proposition 5.9, for all primes
![]() $p \geq 5$
, we prove that there exists a trielliptic curve Y defined over
$p \geq 5$
, we prove that there exists a trielliptic curve Y defined over
![]() ${\overline {\mathbb {F}}}_p$
of genus g and signature
${\overline {\mathbb {F}}}_p$
of genus g and signature
![]() $(r,s)$
whose p-rank is smaller than the upper bound
$(r,s)$
whose p-rank is smaller than the upper bound
![]() $B(r,s)$
.
$B(r,s)$
.
In Theorem 5.11, when
![]() $p \equiv 2 \bmod 3$
is odd, we prove that every integer f satisfying the necessary conditions from Lemma 2.2 occurs as the p-rank of a trielliptic curve Y defined over
$p \equiv 2 \bmod 3$
is odd, we prove that every integer f satisfying the necessary conditions from Lemma 2.2 occurs as the p-rank of a trielliptic curve Y defined over
![]() ${\overline {\mathbb {F}}}_p$
of genus g and signature
${\overline {\mathbb {F}}}_p$
of genus g and signature
![]() $(r,s)$
; in addition, we prove that there is an irreducible component of
$(r,s)$
; in addition, we prove that there is an irreducible component of
![]() ${\mathcal T}_{g, (r,s)}^f$
whose dimension equals the lower bound from Proposition 4.1.
${\mathcal T}_{g, (r,s)}^f$
whose dimension equals the lower bound from Proposition 4.1.
5.1 Notation for trielliptic covers
Suppose
![]() $(Y/S, \iota _0)$
is a smooth trielliptic curve. The
$(Y/S, \iota _0)$
is a smooth trielliptic curve. The
![]() $\mathbb {Z}/3 \mathbb {Z}$
-cover
$\mathbb {Z}/3 \mathbb {Z}$
-cover
![]() $\psi :Y \to \mathbb {P}^1$
has an equation of the form:
$\psi :Y \to \mathbb {P}^1$
has an equation of the form:
 $$ \begin{align} y^3=\prod_{i=1}^{d_1} (x-\alpha_i) \prod_{i=1}^{d_2} (x-\beta_i)^2. \end{align} $$
$$ \begin{align} y^3=\prod_{i=1}^{d_1} (x-\alpha_i) \prod_{i=1}^{d_2} (x-\beta_i)^2. \end{align} $$
Without loss of generality, we assume that
![]() $\psi $
is not branched at
$\psi $
is not branched at
![]() $\infty $
. The number of branch points of
$\infty $
. The number of branch points of
![]() $\psi $
is
$\psi $
is
![]() $n=d_1+d_2$
and the genus of Y is
$n=d_1+d_2$
and the genus of Y is
![]() $g=d_1+d_2-2$
. The inertia type of
$g=d_1+d_2-2$
. The inertia type of
![]() $\psi $
is
$\psi $
is
 ${{\overline {\gamma }}} =(\underbrace {1,\ldots ,1}_{d_1},\underbrace {2,\ldots ,2}_{d_2})$
.
${{\overline {\gamma }}} =(\underbrace {1,\ldots ,1}_{d_1},\underbrace {2,\ldots ,2}_{d_2})$
.
Lemma 5.1 [Reference Achter and Pries3, Lem. 2.7]
The set of inertia types
![]() ${{\overline {\gamma }}} $
for a trielliptic curve
${{\overline {\gamma }}} $
for a trielliptic curve
![]() $(Y/S, \iota _0)$
of genus g is in bijection with
$(Y/S, \iota _0)$
of genus g is in bijection with
![]() $\{(d_1,d_2) \mid d_1,d_2 \in \mathbb {Z}^{\geq 0}, \ d_1+d_2=g+2, \ d_1+2d_2 \equiv 0 \bmod 3\}$
.
$\{(d_1,d_2) \mid d_1,d_2 \in \mathbb {Z}^{\geq 0}, \ d_1+d_2=g+2, \ d_1+2d_2 \equiv 0 \bmod 3\}$
.
There is a
![]() $\mathbb {Z}/3 \mathbb {Z}$
-eigenspace decomposition
$\mathbb {Z}/3 \mathbb {Z}$
-eigenspace decomposition
![]() $H^0(Y, \Omega ^1_Y)= \mathcal {L}_1 \oplus \mathcal {L}_2$
where
$H^0(Y, \Omega ^1_Y)= \mathcal {L}_1 \oplus \mathcal {L}_2$
where
![]() $\omega \in \mathcal {L}_i$
if
$\omega \in \mathcal {L}_i$
if
![]() $\zeta _3 \circ \omega = \zeta _3^i \omega $
. The signature type of
$\zeta _3 \circ \omega = \zeta _3^i \omega $
. The signature type of
![]() $(Y/S, \iota _0)$
is
$(Y/S, \iota _0)$
is
![]() $(r,s)$
where
$(r,s)$
where
![]() $r=\dim (\mathcal {L}_1)$
and
$r=\dim (\mathcal {L}_1)$
and
![]() $s=\dim (\mathcal {L}_2)$
.
$s=\dim (\mathcal {L}_2)$
.
If
![]() $(Y/S, \iota _0)$
is a trielliptic curve, then so is
$(Y/S, \iota _0)$
is a trielliptic curve, then so is
![]() $(Y/S, \iota ^{\prime }_0)$
where
$(Y/S, \iota ^{\prime }_0)$
where
![]() $\iota ^{\prime }_0(1)=\iota _0(2)$
. Replacing
$\iota ^{\prime }_0(1)=\iota _0(2)$
. Replacing
![]() $\iota _0$
with
$\iota _0$
with
![]() $\iota ^{\prime }_0$
exchanges the values of
$\iota ^{\prime }_0$
exchanges the values of
![]() $d_1$
and
$d_1$
and
![]() $d_2$
and the values of r and s.
$d_2$
and the values of r and s.
Definition 5.2. A trielliptic signature for
![]() $g \in \mathbb {N}$
is a pair
$g \in \mathbb {N}$
is a pair
![]() $(r,s)$
of integers with
$(r,s)$
of integers with
![]() $r+s=g$
, and
$r+s=g$
, and
![]() $0 \leq \mathrm {max}\{r,s\} \leq 2 \mathrm {min}\{r,s\}+1$
.
$0 \leq \mathrm {max}\{r,s\} \leq 2 \mathrm {min}\{r,s\}+1$
.
The next result follows from Lemma 2.1
Lemma 5.3. There is a bijection between trielliptic signatures
![]() $(r,s)$
for g and inertia types of
$(r,s)$
for g and inertia types of
![]() $\mathbb {Z}/3 \mathbb {Z}$
-Galois covers of
$\mathbb {Z}/3 \mathbb {Z}$
-Galois covers of
![]() $\mathbb {P}^1$
of genus g given by the formulae
$\mathbb {P}^1$
of genus g given by the formulae
In other words,
![]() $r=(2d_1+d_2-3)/3$
and
$r=(2d_1+d_2-3)/3$
and
![]() $s=(d_1+2d_2-3)/3$
.
$s=(d_1+2d_2-3)/3$
.
Example 5.4 (Signature
 $(1,0)$
, inertia type
$(1,0)$
, inertia type
 ${{\overline {\gamma }}} =(1,1,1)$
)
${{\overline {\gamma }}} =(1,1,1)$
)
There is a unique smooth elliptic curve which is trielliptic. It has p-rank
![]() $0$
when
$0$
when
![]() $p \equiv 2 \bmod 3$
and p-rank
$p \equiv 2 \bmod 3$
and p-rank
![]() $1$
when
$1$
when
![]() $p \equiv 1 \bmod 3$
.
$p \equiv 1 \bmod 3$
.
Proof. By [Reference Silverman22, Th. 10.1], an elliptic curve with automorphism of order
![]() $3$
has j-invariant
$3$
has j-invariant
![]() $0$
. The result follows from [Reference Silverman22, Exer. V.5.7 and Exam. V.4.4].
$0$
. The result follows from [Reference Silverman22, Exer. V.5.7 and Exam. V.4.4].
5.2 Components of the moduli space and maximal p-rank
Let
![]() $(r,s)$
be a trielliptic signature for g. Let
$(r,s)$
be a trielliptic signature for g. Let
![]() ${\overline {\gamma }}$
be the inertia type given by
${\overline {\gamma }}$
be the inertia type given by
![]() ${\overline {\gamma }}(i) = d_i$
where
${\overline {\gamma }}(i) = d_i$
where
![]() $d_i$
are as in Lemma 5.3. Let f be an integer
$d_i$
are as in Lemma 5.3. Let f be an integer
![]() $0 \leq f \leq g$
satisfying the conditions of Lemma 2.2, namely, f is even if
$0 \leq f \leq g$
satisfying the conditions of Lemma 2.2, namely, f is even if
![]() $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
![]() $f \not = g-1$
if
$f \not = g-1$
if
![]() $p \equiv 1 \bmod 3$
.
$p \equiv 1 \bmod 3$
.
Consider the moduli space
![]() ${\mathcal T}_{(r,s)}={\mathcal T}_{3, {\overline {\gamma }}}$
of smooth trielliptic curves with signature
${\mathcal T}_{(r,s)}={\mathcal T}_{3, {\overline {\gamma }}}$
of smooth trielliptic curves with signature
![]() $(r,s)$
and inertia type
$(r,s)$
and inertia type
![]() ${\overline {\gamma }}$
. For f as above, let
${\overline {\gamma }}$
. For f as above, let
![]() ${\mathcal T}_{(r,s)}^f$
denote the p-rank f stratum of
${\mathcal T}_{(r,s)}^f$
denote the p-rank f stratum of
![]() ${\mathcal T}_{(r,s)}$
. Similarly, define
${\mathcal T}_{(r,s)}$
. Similarly, define
![]() ${\overline {{\mathcal T}}}^f_{(r,s)}$
by replacing the word smooth by stable.
${\overline {{\mathcal T}}}^f_{(r,s)}$
by replacing the word smooth by stable.
The next result is a special case of Proposition 4.1.
Proposition 5.5. Suppose
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^f$
. If
${\overline {{\mathcal T}}}_{(r,s)}^f$
. If
![]() $p \equiv 2 \bmod 3$
, then
$p \equiv 2 \bmod 3$
, then
![]() $\mathrm {dim}({\mathcal S}) \geq \mathrm {max}\{r,s\} -1 + f/2$
. If
$\mathrm {dim}({\mathcal S}) \geq \mathrm {max}\{r,s\} -1 + f/2$
. If
![]() $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
![]() $f<g$
, then
$f<g$
, then
![]() $\mathrm {dim}({\mathcal S}) \geq f$
.
$\mathrm {dim}({\mathcal S}) \geq f$
.
We first consider the case of maximal p-rank. Define
![]() $B(r,s)=g$
if
$B(r,s)=g$
if
![]() $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
![]() $B(r,s)=2\min \{r,s\}$
if
$B(r,s)=2\min \{r,s\}$
if
![]() $p \equiv 2 \bmod 3$
. By Theorem 2.3, the p-rank of a trielliptic curve of signature
$p \equiv 2 \bmod 3$
. By Theorem 2.3, the p-rank of a trielliptic curve of signature
![]() $(r,s)$
satisfies
$(r,s)$
satisfies
![]() $f \leq B(r,s)$
.
$f \leq B(r,s)$
.
Proposition 5.6 [Bouw]
If
![]() $p \not = 3$
, then there exists a smooth trielliptic curve with signature
$p \not = 3$
, then there exists a smooth trielliptic curve with signature
![]() $(r,s)$
and p-rank
$(r,s)$
and p-rank
![]() $f_{\mathrm {max}}:=B(r,s)$
. The p-rank
$f_{\mathrm {max}}:=B(r,s)$
. The p-rank
![]() $f_{\mathrm {max}}$
strata
$f_{\mathrm {max}}$
strata
![]() ${\mathcal T}_{(r,s)}^{f_{\mathrm {max}}}$
is open and dense in
${\mathcal T}_{(r,s)}^{f_{\mathrm {max}}}$
is open and dense in
![]() ${\mathcal T}_{(r,s)}$
.
${\mathcal T}_{(r,s)}$
.
Proof. The first statement is a special case of [Reference Bouw7, Props. 7.4 and 7.8]. The second statement follows since
![]() ${\mathcal T}_{(r,s)}$
is irreducible and the p-rank is lower semi-continuous.
${\mathcal T}_{(r,s)}$
is irreducible and the p-rank is lower semi-continuous.
5.3 Base cases
Moonen proved there are exactly 20 families of cyclic covers of
![]() ${\mathbb P}^1$
that are special, meaning that the image of the family under the Torelli morphism is open and dense in the associated unitary Shimura variety; these are listed as
${\mathbb P}^1$
that are special, meaning that the image of the family under the Torelli morphism is open and dense in the associated unitary Shimura variety; these are listed as
![]() $M[1]$
–
$M[1]$
–
![]() $M[20]$
in [Reference Moonen19, Table 1]. In [Reference Li, Mantovan, Pries and Tang17, §§4–6], the authors computed the Newton polygons occurring on these families. In [Reference Li, Mantovan, Pries and Tang17, Th. 5.11] and [Reference Li, Mantovan, Pries and Tang16, Th. 7.1], they proved that each of these Newton polygons occurs for the Jacobian of a smooth curve in the family, except possibly the supersingular ones when p is small.
$M[20]$
in [Reference Moonen19, Table 1]. In [Reference Li, Mantovan, Pries and Tang17, §§4–6], the authors computed the Newton polygons occurring on these families. In [Reference Li, Mantovan, Pries and Tang17, Th. 5.11] and [Reference Li, Mantovan, Pries and Tang16, Th. 7.1], they proved that each of these Newton polygons occurs for the Jacobian of a smooth curve in the family, except possibly the supersingular ones when p is small.
For trielliptic covers, there are three families that are special:
![]() $M[3]$
,
$M[3]$
,
![]() $M[6]$
, and
$M[6]$
, and
![]() $M[10]$
. Since the p-rank is an invariant of the Newton polygon, we can find the dimension of the p-rank strata of these families. When the Newton polygon is supersingular (which happens only when
$M[10]$
. Since the p-rank is an invariant of the Newton polygon, we can find the dimension of the p-rank strata of these families. When the Newton polygon is supersingular (which happens only when
![]() $f=0$
), we can remove the requirement that
$f=0$
), we can remove the requirement that
![]() $p>>0$
in all but one case.
$p>>0$
in all but one case.
The results below for the signature
![]() $(r,s)$
are also true for the signature
$(r,s)$
are also true for the signature
![]() $(s,r)$
.
$(s,r)$
.
Lemma 5.7.
-
1.
 $M[3]$
(Signature
$M[3]$
(Signature
 $(1,1)$
, inertia type
$(1,1)$
, inertia type
 ${\overline {\gamma }} =(1,1,2,2)$
).If
${\overline {\gamma }} =(1,1,2,2)$
).If
 $p \geq 5$
and
$p \geq 5$
and
 $f=0$
, then
$f=0$
, then
 ${\mathcal T}_{(1,1)}^0$
is non-empty of dimension
${\mathcal T}_{(1,1)}^0$
is non-empty of dimension
 $0$
.
$0$
. -
2.
 $M[6]$
(Signature
$M[6]$
(Signature
 $(2,1)$
, inertia type
$(2,1)$
, inertia type
 ${\overline {\gamma }} =(1,1,1,1,2)$
).If
${\overline {\gamma }} =(1,1,1,1,2)$
).If
 $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
 $f = 0,1$
, then
$f = 0,1$
, then
 ${\mathcal T}_{(1,2)}^f$
is non-empty of dimension f.If
${\mathcal T}_{(1,2)}^f$
is non-empty of dimension f.If
 $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
 $f=0$
, then
$f=0$
, then
 ${\mathcal T}_{(1,2)}^f$
is non-empty of dimension
${\mathcal T}_{(1,2)}^f$
is non-empty of dimension
 $1$
.
$1$
. -
3.
 $M[10]$
(Signature
$M[10]$
(Signature
 $(3,1)$
, inertia type
$(3,1)$
, inertia type
 ${\overline {\gamma }} =(1,1,1,1,1,1)$
).If
${\overline {\gamma }} =(1,1,1,1,1,1)$
).If
 $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
 $f=0,1,2$
, then
$f=0,1,2$
, then
 ${\mathcal T}_{(1,3)}^f$
is non-empty of dimension f (if
${\mathcal T}_{(1,3)}^f$
is non-empty of dimension f (if
 $p>>0$
when
$p>>0$
when
 $f=0$
).If
$f=0$
).If
 $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
 $f=0$
, then
$f=0$
, then
 ${\mathcal T}_{(1,3)}^0$
is non-empty of dimension
${\mathcal T}_{(1,3)}^0$
is non-empty of dimension
 $2$
.
$2$
.
Proof. The Newton polygons for the curves in the family are listed on [Reference Li, Mantovan, Pries and Tang17, p. 19].
-
1. When
 $f=0$
, then the Newton polygon of a curve in the family is supersingular. If
$f=0$
, then the Newton polygon of a curve in the family is supersingular. If
 $p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang17, Th. 5.11]. The main idea is that, because of Example 5.4, a supersingular curve in the family must be smooth.When
$p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang17, Th. 5.11]. The main idea is that, because of Example 5.4, a supersingular curve in the family must be smooth.When
 $p \equiv 2 \bmod 3$
is odd, the result follows from Lemma 7.1 (or [Reference Li, Mantovan, Pries and Tang16, Th. 7.1] when
$p \equiv 2 \bmod 3$
is odd, the result follows from Lemma 7.1 (or [Reference Li, Mantovan, Pries and Tang16, Th. 7.1] when
 $p>>0$
).
$p>>0$
). -
2. When
 $p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang17, Th. 5.11]; note that the Newton polygon has slopes
$p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang17, Th. 5.11]; note that the Newton polygon has slopes
 $1/3$
and
$1/3$
and
 $2/3$
when
$2/3$
when
 $f=0$
.When
$f=0$
.When
 $p \equiv 2 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang16, Th. 7.1] when
$p \equiv 2 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang16, Th. 7.1] when
 $p>>0$
. Here is an argument that removes the hypothesis
$p>>0$
. Here is an argument that removes the hypothesis
 $p>>0$
. Let S be an irreducible component of the p-rank
$p>>0$
. Let S be an irreducible component of the p-rank
 $0$
locus
$0$
locus
 ${\overline {{\mathcal T}}}_{(2,1)}^0$
. Then
${\overline {{\mathcal T}}}_{(2,1)}^0$
. Then
 $\mathrm {dim}(S)=1$
because
$\mathrm {dim}(S)=1$
because
 ${\overline {{\mathcal T}}}_{(2,1)}$
has dimension
${\overline {{\mathcal T}}}_{(2,1)}$
has dimension
 $2$
and its generic geometric point represents a curve with p-rank
$2$
and its generic geometric point represents a curve with p-rank
 $2$
. The intersection of S with the boundary is contained in
$2$
. The intersection of S with the boundary is contained in
 $\kappa _{1,2}({\widetilde {{\mathcal T}}}_{(1,0)}^0 \times {\widetilde {{\mathcal T}}}_{(1,1)}^0)$
, but that only has dimension
$\kappa _{1,2}({\widetilde {{\mathcal T}}}_{(1,0)}^0 \times {\widetilde {{\mathcal T}}}_{(1,1)}^0)$
, but that only has dimension
 $0$
, so the generic geometric point of S represents a smooth curve.
$0$
, so the generic geometric point of S represents a smooth curve. -
3. When
 $p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang16, Th. 7.1]; we do not know how to remove the hypothesis
$p \equiv 1 \bmod 3$
, the result follows from [Reference Li, Mantovan, Pries and Tang16, Th. 7.1]; we do not know how to remove the hypothesis
 $p>>0$
when
$p>>0$
when
 $f=0$
.When
$f=0$
.When
 $p \equiv 2 \bmod 3$
, then
$p \equiv 2 \bmod 3$
, then
 ${\mathcal T}_{(1,3)}^0$
is non-empty of dimension
${\mathcal T}_{(1,3)}^0$
is non-empty of dimension
 $2$
by [Reference Li, Mantovan, Pries and Tang17, Th. 5.11].
$2$
by [Reference Li, Mantovan, Pries and Tang17, Th. 5.11].
For the family
![]() $M[10]$
, we consider the unitary Shimura variety
$M[10]$
, we consider the unitary Shimura variety
![]() $\mathrm {Sh}$
attached to the data of
$\mathrm {Sh}$
attached to the data of
![]() $\ell =3$
and the signature type
$\ell =3$
and the signature type
![]() $(3,1)$
. As in §3.5, let
$(3,1)$
. As in §3.5, let
![]() $\Sigma $
be the irreducible component of
$\Sigma $
be the irreducible component of
![]() $\mathrm {Sh}$
which contains the Torelli locus.
$\mathrm {Sh}$
which contains the Torelli locus.
Proposition 5.8. Suppose
![]() $p \equiv 2 \bmod 3$
. For the family
$p \equiv 2 \bmod 3$
. For the family
![]() $M[10]$
, the p-rank
$M[10]$
, the p-rank
![]() $0$
stratum
$0$
stratum
![]() $\Sigma ^0$
of
$\Sigma ^0$
of
![]() $\Sigma $
is irreducible and thus
$\Sigma $
is irreducible and thus
![]() ${\mathcal T}_{(1,3)}^0$
is irreducible.
${\mathcal T}_{(1,3)}^0$
is irreducible.
Proof. For each generic geometric point of
![]() $\Sigma ^0$
, we consider the Newton polygon
$\Sigma ^0$
, we consider the Newton polygon
![]() $\nu $
of the abelian variety represented by this point. Applying the Kottwitz method (see [Reference Li, Mantovan, Pries and Tang17, §4.3 and table on p. 19]) shows that
$\nu $
of the abelian variety represented by this point. Applying the Kottwitz method (see [Reference Li, Mantovan, Pries and Tang17, §4.3 and table on p. 19]) shows that
![]() $\nu $
has slopes
$\nu $
has slopes
![]() $1/4$
and
$1/4$
and
![]() $3/4$
when
$3/4$
when
![]() $p \equiv 2 \bmod 3$
; in particular, it is not supersingular. The hypotheses of [Reference Achter1, Th. 1.1] are satisfied; the conclusion of that result is that the stratum of
$p \equiv 2 \bmod 3$
; in particular, it is not supersingular. The hypotheses of [Reference Achter1, Th. 1.1] are satisfied; the conclusion of that result is that the stratum of
![]() $\Sigma $
with Newton polygon
$\Sigma $
with Newton polygon
![]() $\nu $
is irreducible. Since this stratum is open and dense in
$\nu $
is irreducible. Since this stratum is open and dense in
![]() $\Sigma ^0$
, this implies that
$\Sigma ^0$
, this implies that
![]() $\Sigma ^0$
is irreducible.
$\Sigma ^0$
is irreducible.
Since the family
![]() $M[10]$
is special, the image of
$M[10]$
is special, the image of
![]() ${\mathcal T}_{(3,1)}$
is open and dense in
${\mathcal T}_{(3,1)}$
is open and dense in
![]() $\Sigma $
. It follows that
$\Sigma $
. It follows that
![]() ${\mathcal T}_{(3,1)}^0$
is open and dense in
${\mathcal T}_{(3,1)}^0$
is open and dense in
![]() $\Sigma ^0$
. Thus,
$\Sigma ^0$
. Thus,
![]() ${\mathcal T}_{(3,1)}^0$
is irreducible as well.
${\mathcal T}_{(3,1)}^0$
is irreducible as well.
5.4 Trielliptic curves whose p-rank is not maximal
The next result extends Proposition 5.6 by showing, for each prime
![]() $p \geq 5$
, that there exist trielliptic curves of each signature type
$p \geq 5$
, that there exist trielliptic curves of each signature type
![]() $(r,s)$
whose p-rank is not the maximum
$(r,s)$
whose p-rank is not the maximum
![]() $B(r,s)$
. Recall that
$B(r,s)$
. Recall that
![]() $B(r,s) = 2 \mathrm {min}\{r,s\}$
when
$B(r,s) = 2 \mathrm {min}\{r,s\}$
when
![]() $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
![]() $B(r,s)=r+s$
when
$B(r,s)=r+s$
when
![]() $p \equiv 1 \bmod 3$
.
$p \equiv 1 \bmod 3$
.
Proposition 5.9. Let
![]() $p \geq 5$
and
$p \geq 5$
and
![]() $g \geq 2$
. Let
$g \geq 2$
. Let
![]() $(r,s)$
be a trielliptic signature for g. Then
$(r,s)$
be a trielliptic signature for g. Then
![]() ${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, and each of its irreducible components has dimension
${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, and each of its irreducible components has dimension
![]() $g-2$
(codimension
$g-2$
(codimension
![]() $1$
in
$1$
in
![]() ${\mathcal T}_{(r,s)}$
). Thus, there exists a smooth trielliptic curve with signature
${\mathcal T}_{(r,s)}$
). Thus, there exists a smooth trielliptic curve with signature
![]() $(r,s)$
and p-rank
$(r,s)$
and p-rank
![]() $f=B(r,s)-2$
.
$f=B(r,s)-2$
.
Proof. Recall that
![]() $\mathrm {dim}({\mathcal T}_{(r,s)})=g-1$
and the generic geometric point of
$\mathrm {dim}({\mathcal T}_{(r,s)})=g-1$
and the generic geometric point of
![]() ${\mathcal T}_{(r,s)}$
represents a trielliptic curve with p-rank
${\mathcal T}_{(r,s)}$
represents a trielliptic curve with p-rank
![]() $B(r,s)$
by Proposition 5.6. If
$B(r,s)$
by Proposition 5.6. If
![]() ${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, then, by definition, each of its generic geometric points represents a smooth trielliptic curve with signature
${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, then, by definition, each of its generic geometric points represents a smooth trielliptic curve with signature
![]() $(r,s)$
and p-rank
$(r,s)$
and p-rank
![]() $f=B(r,s)-2$
. Furthermore, if
$f=B(r,s)-2$
. Furthermore, if
![]() ${\mathcal S}$
is one of the irreducible components of
${\mathcal S}$
is one of the irreducible components of
![]() ${\mathcal T}_{(r,s)}^{B(r,s)-2}$
, then
${\mathcal T}_{(r,s)}^{B(r,s)-2}$
, then
![]() $\mathrm {dim}({\mathcal S}) \leq g-2$
and Proposition 5.5 implies that
$\mathrm {dim}({\mathcal S}) \leq g-2$
and Proposition 5.5 implies that
![]() $\mathrm {dim}({\mathcal S}) \geq g-2$
, so
$\mathrm {dim}({\mathcal S}) \geq g-2$
, so
![]() $\mathrm {dim}(S)=g-2$
.
$\mathrm {dim}(S)=g-2$
.
It thus suffices to prove that
![]() ${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty. Without loss of generality, suppose
${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty. Without loss of generality, suppose
![]() $r \leq s$
. The proof is by induction on r.
$r \leq s$
. The proof is by induction on r.
If
![]() $r=1$
, then
$r=1$
, then
![]() $1 \leq s \leq 3$
. If
$1 \leq s \leq 3$
. If
![]() $r=1$
and
$r=1$
and
![]() $s=1$
, then
$s=1$
, then
![]() $B(1,1)-2=0$
and the result follows from Lemma 5.7(1) (deferred to Lemma 7.1(1) when
$B(1,1)-2=0$
and the result follows from Lemma 5.7(1) (deferred to Lemma 7.1(1) when
![]() $p \equiv 2 \bmod 3$
). If
$p \equiv 2 \bmod 3$
). If
![]() $r=1$
and
$r=1$
and
![]() $s=2$
, then
$s=2$
, then
![]() $B(1,2)-2=1$
when
$B(1,2)-2=1$
when
![]() $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
![]() $B(1,2)-2=0$
when
$B(1,2)-2=0$
when
![]() $p \equiv 2 \bmod 3$
and the result follows from Lemma 5.7(2). If
$p \equiv 2 \bmod 3$
and the result follows from Lemma 5.7(2). If
![]() $r=1$
and
$r=1$
and
![]() $s=3$
, then
$s=3$
, then
![]() $B(1,3)-2=2$
when
$B(1,3)-2=2$
when
![]() $p \equiv 1 \bmod 3$
and
$p \equiv 1 \bmod 3$
and
![]() $B(1,3)-2=0$
when
$B(1,3)-2=0$
when
![]() $p \equiv 2 \bmod 3$
, and the result follows from Lemma 5.7(3).
$p \equiv 2 \bmod 3$
, and the result follows from Lemma 5.7(3).
Now, suppose
![]() $2 \leq r \leq s$
.
$2 \leq r \leq s$
.
Case 1: Suppose
![]() $s \leq 2r$
. Then
$s \leq 2r$
. Then
![]() $(r-1,s-1)$
is a valid trielliptic signature. Note that
$(r-1,s-1)$
is a valid trielliptic signature. Note that
![]() $B(r-1,s-1)=B(r,s)-2$
. Let
$B(r-1,s-1)=B(r,s)-2$
. Let
![]() ${\mathcal S}_1$
be an irreducible component of
${\mathcal S}_1$
be an irreducible component of
![]() ${\mathcal T}_{(1,1)}^0$
, which is non-empty when
${\mathcal T}_{(1,1)}^0$
, which is non-empty when
![]() $p \geq 5$
by Lemma 5.7(1). Let
$p \geq 5$
by Lemma 5.7(1). Let
![]() ${\mathcal S}_2$
be an irreducible component of
${\mathcal S}_2$
be an irreducible component of
![]() ${\mathcal T}_{(r-1,s-1)}^{B(r-1,s-1)}$
, which is non-empty by Proposition 5.6. Consider an irreducible component
${\mathcal T}_{(r-1,s-1)}^{B(r-1,s-1)}$
, which is non-empty by Proposition 5.6. Consider an irreducible component
![]() ${\widetilde {\mathcal S}}_1$
of
${\widetilde {\mathcal S}}_1$
of
![]() ${\widetilde {{\mathcal T}}}_{(1,1)}^0$
lying above
${\widetilde {{\mathcal T}}}_{(1,1)}^0$
lying above
![]() ${\mathcal S}_1$
and an irreducible component
${\mathcal S}_1$
and an irreducible component
![]() ${\widetilde {\mathcal S}}_2$
of
${\widetilde {\mathcal S}}_2$
of
![]() ${\widetilde {{\mathcal T}}}_{(r-1,s-1)}^{B(r-1,s-1)}$
lying above
${\widetilde {{\mathcal T}}}_{(r-1,s-1)}^{B(r-1,s-1)}$
lying above
![]() ${\mathcal S}_2$
.
${\mathcal S}_2$
.
When
![]() $(r,s)=(1,1)$
, then
$(r,s)=(1,1)$
, then
![]() $d_1=d_2=2$
are both positive. Thus, without loss of generality, we can choose
$d_1=d_2=2$
are both positive. Thus, without loss of generality, we can choose
![]() ${\widetilde {\mathcal S}}_1$
(the labeling of the ramification points) so that the clutching situation below is admissible:
${\widetilde {\mathcal S}}_1$
(the labeling of the ramification points) so that the clutching situation below is admissible:
Let
![]() $K=\kappa _{2, g-2}({\widetilde {{\mathcal S}}}_1 \times {\widetilde {{\mathcal S}}}_2)$
. By construction, K is contained in
$K=\kappa _{2, g-2}({\widetilde {{\mathcal S}}}_1 \times {\widetilde {{\mathcal S}}}_2)$
. By construction, K is contained in
![]() $\Delta _2[{\overline {{\mathcal T}}}_{(r,s)}^{B(r,s) - 2}]$
.
$\Delta _2[{\overline {{\mathcal T}}}_{(r,s)}^{B(r,s) - 2}]$
.
Let W be an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^{B(r,s) - 2}$
which contains K. By the same reasoning as the first paragraph of the proof,
${\overline {{\mathcal T}}}_{(r,s)}^{B(r,s) - 2}$
which contains K. By the same reasoning as the first paragraph of the proof,
![]() $\mathrm {dim}(W) = g-2$
. On the other hand, since
$\mathrm {dim}(W) = g-2$
. On the other hand, since
![]() $\mathrm {dim}({\widetilde {{\mathcal S}}}_1)=0$
and
$\mathrm {dim}({\widetilde {{\mathcal S}}}_1)=0$
and
![]() $\mathrm {dim}({\widetilde {{\mathcal T}}}_{(r-1,s-1)}) = g-3$
, it follows that
$\mathrm {dim}({\widetilde {{\mathcal T}}}_{(r-1,s-1)}) = g-3$
, it follows that
Thus, the generic point of W is not contained in K.
By construction, the generic point of
![]() ${\mathcal S}_1$
represents a smooth curve. The generic point of
${\mathcal S}_1$
represents a smooth curve. The generic point of
![]() ${\overline {{\mathcal T}}}_{(r-1,s-1)}^{B(r-1,s-1)}$
represents a smooth curve by Proposition 5.6 and Lemma 3.2. So the generic point of W is not contained in any other boundary component. Thus, the generic point of W represents a smooth curve and
${\overline {{\mathcal T}}}_{(r-1,s-1)}^{B(r-1,s-1)}$
represents a smooth curve by Proposition 5.6 and Lemma 3.2. So the generic point of W is not contained in any other boundary component. Thus, the generic point of W represents a smooth curve and
![]() ${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, with irreducible components of dimension
${\mathcal T}_{(r,s)}^{B(r,s)-2}$
is non-empty, with irreducible components of dimension
![]() $g-2$
.
$g-2$
.
Case 2: Suppose
![]() $s = 2r+1$
. Then
$s = 2r+1$
. Then
![]() $(r-1,s-2)$
is a valid trielliptic signature. Note that
$(r-1,s-2)$
is a valid trielliptic signature. Note that
![]() $B(r-1,s-2)=2(r-1)$
when
$B(r-1,s-2)=2(r-1)$
when
![]() $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
![]() $B(r-1,s-2)=g-3$
when
$B(r-1,s-2)=g-3$
when
![]() $p \equiv 1 \bmod 3$
. Let
$p \equiv 1 \bmod 3$
. Let
![]() $f'=0$
when
$f'=0$
when
![]() $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
![]() $f'=1$
when
$f'=1$
when
![]() $p \equiv 1 \bmod 3$
. Then
$p \equiv 1 \bmod 3$
. Then
![]() $f'+ B(r-1,s-2)=B(r,s)-2$
.
$f'+ B(r-1,s-2)=B(r,s)-2$
.
Let
![]() ${\mathcal S}_1$
be an irreducible component of
${\mathcal S}_1$
be an irreducible component of
![]() ${\mathcal T}_{(1,2)}^{f'}$
, which is non-empty by Lemma 5.7(2). Let
${\mathcal T}_{(1,2)}^{f'}$
, which is non-empty by Lemma 5.7(2). Let
![]() ${\mathcal S}_2$
be an irreducible component of
${\mathcal S}_2$
be an irreducible component of
![]() ${\mathcal T}_{(r-1,s-2)}^{B(r-1,s-2)}$
, which is non-empty by Proposition 5.6.
${\mathcal T}_{(r-1,s-2)}^{B(r-1,s-2)}$
, which is non-empty by Proposition 5.6.
When
![]() $(r,s)=(1,2)$
, then
$(r,s)=(1,2)$
, then
![]() $d_1=1$
and
$d_1=1$
and
![]() $d_2=4$
, which are both positive. We repeat the argument above, making an admissible clutching of the following form:
$d_2=4$
, which are both positive. We repeat the argument above, making an admissible clutching of the following form:
The rest of the proof is the same.
Remark 5.10. When
![]() $p=2$
, then
$p=2$
, then
![]() ${\mathcal T}_{(1,1)}^0$
is empty, as shown in Lemma 7.1(2). When
${\mathcal T}_{(1,1)}^0$
is empty, as shown in Lemma 7.1(2). When
![]() $p=2$
, it is still true that
$p=2$
, it is still true that
![]() ${\overline {{\mathcal T}}}_{(1,1)}^0$
is non-empty (of dimension
${\overline {{\mathcal T}}}_{(1,1)}^0$
is non-empty (of dimension
![]() $0$
); the same proof as for Proposition 5.9 shows that
$0$
); the same proof as for Proposition 5.9 shows that
![]() ${\overline {{\mathcal T}}}_{(r,s)}^{B(r,s)-2}$
is non-empty and each of its irreducible components has dimension
${\overline {{\mathcal T}}}_{(r,s)}^{B(r,s)-2}$
is non-empty and each of its irreducible components has dimension
![]() $g-2$
(codimension
$g-2$
(codimension
![]() $1$
in
$1$
in
![]() ${\overline {{\mathcal T}}}_{(r,s)}$
), but it is not clear whether any of its points represents a smooth curve.
${\overline {{\mathcal T}}}_{(r,s)}$
), but it is not clear whether any of its points represents a smooth curve.
The case when
![]() $p=3$
is described in Proposition 7.4.
$p=3$
is described in Proposition 7.4.
5.5 Existence of trielliptic curves with given p-rank
In this section, suppose
![]() $p \equiv 2 \bmod 3$
. In this case, the necessary conditions on the p-rank are that f is even and
$p \equiv 2 \bmod 3$
. In this case, the necessary conditions on the p-rank are that f is even and
![]() $0 \leq f \leq 2\mathrm {min}(r,s)$
. For every signature type and for all odd
$0 \leq f \leq 2\mathrm {min}(r,s)$
. For every signature type and for all odd
![]() $p \equiv 2 \bmod 3$
, we prove that every p-rank f satisfying the necessary conditions occurs for a smooth trielliptic curve of that signature in characteristic p. If
$p \equiv 2 \bmod 3$
, we prove that every p-rank f satisfying the necessary conditions occurs for a smooth trielliptic curve of that signature in characteristic p. If
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^f$
, recall from Proposition 5.5 that
${\overline {{\mathcal T}}}_{(r,s)}^f$
, recall from Proposition 5.5 that
![]() $\mathrm {dim}({\mathcal S}) \geq \mathrm {max}\{r,s\} -1 + f/2$
.
$\mathrm {dim}({\mathcal S}) \geq \mathrm {max}\{r,s\} -1 + f/2$
.
Theorem 5.11. Let
![]() $p \equiv 2 \bmod 3$
be odd, and let
$p \equiv 2 \bmod 3$
be odd, and let
![]() $g \geq 2$
. Let
$g \geq 2$
. Let
![]() $(r,s)$
be a trielliptic signature for g. Suppose
$(r,s)$
be a trielliptic signature for g. Suppose
![]() $0 \leq f \leq 2\mathrm {min}\{r,s\}$
is even. Then there exists a smooth trielliptic curve of genus g defined over
$0 \leq f \leq 2\mathrm {min}\{r,s\}$
is even. Then there exists a smooth trielliptic curve of genus g defined over
![]() ${\overline {\mathbb {F}}}_p$
with signature type
${\overline {\mathbb {F}}}_p$
with signature type
![]() $(r,s)$
and p-rank f. More generally,
$(r,s)$
and p-rank f. More generally,
![]() ${\mathcal T}_{(r,s)}^f$
is non-empty and contains an irreducible component
${\mathcal T}_{(r,s)}^f$
is non-empty and contains an irreducible component
![]() ${\mathcal S}={\mathcal S}_{(r,s)}^f$
with
${\mathcal S}={\mathcal S}_{(r,s)}^f$
with
![]() $\dim ({\mathcal S}) = \max \{r,s\}-1 +f/2$
.
$\dim ({\mathcal S}) = \max \{r,s\}-1 +f/2$
.
Proof. The first statement about the existence of the trielliptic curve with signature type
![]() $(r,s)$
and p-rank f is equivalent to the statement that
$(r,s)$
and p-rank f is equivalent to the statement that
![]() ${\mathcal T}_{(r,s)}^f$
is non-empty.
${\mathcal T}_{(r,s)}^f$
is non-empty.
To prove this, without loss of generality, suppose
![]() $r \leq s$
. The proof is by induction on r, with the result being true for
$r \leq s$
. The proof is by induction on r, with the result being true for
![]() $r=1$
by Proposition 5.6 when
$r=1$
by Proposition 5.6 when
![]() $f=2$
and Lemma 5.7 when
$f=2$
and Lemma 5.7 when
![]() $f=0$
. Suppose the result is true for all trielliptic signatures
$f=0$
. Suppose the result is true for all trielliptic signatures
![]() $(r_1,s_1)$
with
$(r_1,s_1)$
with
![]() $1 \leq r_1 < r$
.
$1 \leq r_1 < r$
.
Let
![]() $(r_2,s_2)$
be either (i)
$(r_2,s_2)$
be either (i)
![]() $(1,2)$
or (ii)
$(1,2)$
or (ii)
![]() $(1,1)$
, with choice (i) mandated if
$(1,1)$
, with choice (i) mandated if
![]() $s=2r+1$
and choice (ii) mandated if
$s=2r+1$
and choice (ii) mandated if
![]() $s=r$
. Let
$s=r$
. Let
![]() $g_2=r_2+s_2$
. Let
$g_2=r_2+s_2$
. Let
![]() $r_1=r-r_2$
and
$r_1=r-r_2$
and
![]() $s_1=s-s_2$
, and
$s_1=s-s_2$
, and
![]() $g_1=r_1+s_1$
. Note that
$g_1=r_1+s_1$
. Note that
![]() $(r_1,s_1)$
is a trielliptic signature for
$(r_1,s_1)$
is a trielliptic signature for
![]() $g_1$
and
$g_1$
and
![]() $r_1 \leq s_1$
.
$r_1 \leq s_1$
.
By the hypothesis,
![]() $0 \leq f \leq 2r$
is even. Let
$0 \leq f \leq 2r$
is even. Let
![]() $f_2$
be either (a) 2 or (b) 0, with choice (a) mandated if
$f_2$
be either (a) 2 or (b) 0, with choice (a) mandated if
![]() $f=2r$
and choice (b) mandated if
$f=2r$
and choice (b) mandated if
![]() $f=0$
. Let
$f=0$
. Let
![]() $f_1=f-f_2$
. Then
$f_1=f-f_2$
. Then
![]() $0 \leq f_1 \leq 2r_1$
and
$0 \leq f_1 \leq 2r_1$
and
![]() $f_1$
is even.
$f_1$
is even.
It follows that
![]() ${\mathcal T}_{(r_i,s_i)}^{f_i}$
is non-empty and contains an irreducible component
${\mathcal T}_{(r_i,s_i)}^{f_i}$
is non-empty and contains an irreducible component
![]() ${\mathcal S}_i$
with
${\mathcal S}_i$
with
![]() $\dim ({\mathcal S}_i) = s_i-1 +f_i/2$
(by the inductive hypothesis when
$\dim ({\mathcal S}_i) = s_i-1 +f_i/2$
(by the inductive hypothesis when
![]() $i=1$
, Propositions 5.6 and 5.9 when
$i=1$
, Propositions 5.6 and 5.9 when
![]() $i=2$
). One can add a labeling of the smooth ramification points by choosing an irreducible component
$i=2$
). One can add a labeling of the smooth ramification points by choosing an irreducible component
![]() $\tilde {{\mathcal S}}_i$
of
$\tilde {{\mathcal S}}_i$
of
![]() $\tilde {{\mathcal T}}_{(r_i,s_i)}$
above
$\tilde {{\mathcal T}}_{(r_i,s_i)}$
above
![]() ${\mathcal S}_i$
.
${\mathcal S}_i$
.
By construction,
![]() $K=\kappa _{g_1, g_2}(\tilde {{\mathcal S}}_1 \times \tilde {{\mathcal S}}_2)$
is contained in
$K=\kappa _{g_1, g_2}(\tilde {{\mathcal S}}_1 \times \tilde {{\mathcal S}}_2)$
is contained in
![]() $\overline {{\mathcal T}}_{(r,s)}^f$
and
$\overline {{\mathcal T}}_{(r,s)}^f$
and
Then K is contained in a component W of
![]() $\overline {{\mathcal T}}_{(r,s)}^f$
. By Proposition 5.5,
$\overline {{\mathcal T}}_{(r,s)}^f$
. By Proposition 5.5,
![]() $\mathrm {dim}(W) \geq s-1 + f/2$
. By Proposition 3.3,
$\mathrm {dim}(W) \geq s-1 + f/2$
. By Proposition 3.3,
![]() $\mathrm {dim}(W) \leq s-1 + f/2$
. Thus,
$\mathrm {dim}(W) \leq s-1 + f/2$
. Thus,
![]() $\mathrm {dim}(W) = s-1 + f/2$
.
$\mathrm {dim}(W) = s-1 + f/2$
.
Finally, the generic point of W is not contained in K. Since the generic points of
![]() ${\mathcal S}_1$
and
${\mathcal S}_1$
and
![]() ${\mathcal S}_2$
represent smooth curves (this requires the hypothesis
${\mathcal S}_2$
represent smooth curves (this requires the hypothesis
![]() $p \not = 2$
for case (ii)), the generic point of W is not contained in any other boundary component. Thus, the generic point of W represents a smooth curve. It follows that
$p \not = 2$
for case (ii)), the generic point of W is not contained in any other boundary component. Thus, the generic point of W represents a smooth curve. It follows that
![]() ${\mathcal S}=W \cap {\mathcal T}_{(r,s)}^f$
is open and dense in W and thus is non-empty with dimension
${\mathcal S}=W \cap {\mathcal T}_{(r,s)}^f$
is open and dense in W and thus is non-empty with dimension
![]() $s-1 + f/2$
.
$s-1 + f/2$
.
Remark 5.12. When
![]() $p \equiv 1 \bmod 3$
, we were not able to prove an analogue of Theorem 5.11. Then main reason is that if
$p \equiv 1 \bmod 3$
, we were not able to prove an analogue of Theorem 5.11. Then main reason is that if
![]() $f< g$
and if
$f< g$
and if
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^f$
, then Proposition 5.5 states that
${\overline {{\mathcal T}}}_{(r,s)}^f$
, then Proposition 5.5 states that
![]() $\mathrm {dim}({\mathcal S}) \geq f$
. When
$\mathrm {dim}({\mathcal S}) \geq f$
. When
![]() $f=0$
, the expected dimension is
$f=0$
, the expected dimension is
![]() $0$
, which makes it difficult to work with the p-rank
$0$
, which makes it difficult to work with the p-rank
![]() $0$
stratum inductively.
$0$
stratum inductively.
6 Cases where all p-rank
 $0$
strata have the same dimension
$0$
strata have the same dimension
Suppose
![]() $p \equiv 2 \bmod 3$
is odd. Let
$p \equiv 2 \bmod 3$
is odd. Let
![]() $g \geq 2$
. Let
$g \geq 2$
. Let
![]() $(r,s)$
be a trielliptic signature for g. Let f be an even integer such that
$(r,s)$
be a trielliptic signature for g. Let f be an even integer such that
![]() $0 \leq f \leq 2\mathrm {min}\{r,s\}$
. If
$0 \leq f \leq 2\mathrm {min}\{r,s\}$
. If
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\mathcal T}_{(r,s)}^f$
, then
${\mathcal T}_{(r,s)}^f$
, then
![]() $\dim ({\mathcal S}) \geq \max \{r,s\}-1 +f/2$
by Proposition 5.5.
$\dim ({\mathcal S}) \geq \max \{r,s\}-1 +f/2$
by Proposition 5.5.
We proved in Theorem 5.11 that
![]() ${\mathcal T}_{(r,s)}^f$
is non-empty and contains an irreducible component with
${\mathcal T}_{(r,s)}^f$
is non-empty and contains an irreducible component with
![]() $\dim ({\mathcal S}) = \max \{r,s\}-1 +f/2$
. Motivated by a result in the hyperelliptic case [Reference Glass and Pries11, Prop. 2], we tried to prove that every component of
$\dim ({\mathcal S}) = \max \{r,s\}-1 +f/2$
. Motivated by a result in the hyperelliptic case [Reference Glass and Pries11, Prop. 2], we tried to prove that every component of
![]() ${\mathcal T}_{(r,s)}^f$
has the same dimension. This is true when
${\mathcal T}_{(r,s)}^f$
has the same dimension. This is true when
![]() $\mathrm {min}\{r, s\} =1$
by Lemma 5.7. In this section, we prove it is also true when
$\mathrm {min}\{r, s\} =1$
by Lemma 5.7. In this section, we prove it is also true when
![]() $\mathrm {min}\{r, s\} = 2$
(see Corollary 6.4).
$\mathrm {min}\{r, s\} = 2$
(see Corollary 6.4).
Here are some of the reasons the trielliptic case is more difficult than the hyperelliptic case. First, it is possible that there are components of
![]() ${\overline {{\mathcal T}}}_{r,s}^f$
that are fully contained in the boundary. This does not happen in the hyperelliptic case by [Reference Achter and Pries5, Lem. 3.2]. We describe this in §7.2.
${\overline {{\mathcal T}}}_{r,s}^f$
that are fully contained in the boundary. This does not happen in the hyperelliptic case by [Reference Achter and Pries5, Lem. 3.2]. We describe this in §7.2.
Second, in the hyperelliptic case, every irreducible component of the p-rank
![]() $0$
stratum
$0$
stratum
![]() ${\overline {{\mathcal H}}}^0_g$
contains the moduli point of a tree of g (supersingular) elliptic curves [Reference Achter and Pries5, Th. 3.11(c)]. The analogous result in the trielliptic case is weaker. By Theorem 4.3, every irreducible component of
${\overline {{\mathcal H}}}^0_g$
contains the moduli point of a tree of g (supersingular) elliptic curves [Reference Achter and Pries5, Th. 3.11(c)]. The analogous result in the trielliptic case is weaker. By Theorem 4.3, every irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^0$
contains the moduli point of a tree of
${\overline {{\mathcal T}}}_{(r,s)}^0$
contains the moduli point of a tree of
![]() $\mathrm {max}\{r,s\}$
trielliptic curves, but
$\mathrm {max}\{r,s\}$
trielliptic curves, but
![]() $\mathrm {max}\{r,s\}$
is strictly less than g.
$\mathrm {max}\{r,s\}$
is strictly less than g.
6.1 Balanced degenerations
In this section, we introduce balanced degenerations which are helpful for finding an upper bound for the dimension of irreducible components. The reason for the balanced condition is that
![]() $B(r,s)$
is not additive in general. When
$B(r,s)$
is not additive in general. When
![]() $p \equiv 2 \bmod 3$
and
$p \equiv 2 \bmod 3$
and
![]() $r \leq s$
, then
$r \leq s$
, then
![]() $B(r,s)=B(r_1,s_1)+B(r_2,s_2)$
if and only if
$B(r,s)=B(r_1,s_1)+B(r_2,s_2)$
if and only if
![]() $r_1 \leq s_1$
and
$r_1 \leq s_1$
and
![]() $r_2 \leq s_2$
.
$r_2 \leq s_2$
.
Definition 6.1. Let S be an irreducible component of
![]() ${\overline {{\mathcal T}}}^f_{(r,s)}$
with
${\overline {{\mathcal T}}}^f_{(r,s)}$
with
![]() $r \leq s$
. We say S degenerates to
$r \leq s$
. We say S degenerates to
![]() $\Delta ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
if S intersects
$\Delta ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
if S intersects
![]() $\kappa (\tilde {\mathcal T}^{f_1}_{(r_1,s_1)} \times \tilde {\mathcal T}^{f_2}_{(r_2,s_2)})$
.
$\kappa (\tilde {\mathcal T}^{f_1}_{(r_1,s_1)} \times \tilde {\mathcal T}^{f_2}_{(r_2,s_2)})$
.
We say the degeneration is balanced if
![]() $r_1 \leq s_1$
and
$r_1 \leq s_1$
and
![]() $r_2 \leq s_2$
.
$r_2 \leq s_2$
.
In Definition 6.1, we implicitly require that
![]() $(r_1,s_1)$
and
$(r_1,s_1)$
and
![]() $(r_2,s_2)$
are trielliptic signatures, that
$(r_2,s_2)$
are trielliptic signatures, that
![]() $r_1+r_2=r$
and
$r_1+r_2=r$
and
![]() $s_1+s_2=s$
, that
$s_1+s_2=s$
, that
![]() $f_i$
are even with
$f_i$
are even with
![]() $0 \leq f_i \leq 2r_i$
, and that
$0 \leq f_i \leq 2r_i$
, and that
![]() $f_1 + f_2 \leq f$
.
$f_1 + f_2 \leq f$
.
Proposition 6.2. Suppose S has a balanced degeneration to
![]() $\Delta ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
. Suppose, for
$\Delta ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
. Suppose, for
![]() $i=1,2$
, that
$i=1,2$
, that
Then
![]() $\dim (S)= s-1 +f/2$
and S contains
$\dim (S)= s-1 +f/2$
and S contains
![]() $\kappa (S_1 \times S_2)$
, where
$\kappa (S_1 \times S_2)$
, where
![]() $S_i$
denotes a component of
$S_i$
denotes a component of
![]() $\tilde {\mathcal T}^{f_i}_{(r_i,s_i)}$
for
$\tilde {\mathcal T}^{f_i}_{(r_i,s_i)}$
for
![]() $i=1,2$
.
$i=1,2$
.
Proof. By Theorem 5.5,
![]() $\dim (S) \geq s - 1 +f/2$
. By Proposition 3.3,
$\dim (S) \geq s - 1 +f/2$
. By Proposition 3.3,
Since the degeneration is balanced,
![]() $r_i \leq s_i$
. By hypothesis,
$r_i \leq s_i$
. By hypothesis,
So,
Thus,
![]() $\dim (S) = s-1+f/2$
. Furthermore, S contains
$\dim (S) = s-1+f/2$
. Furthermore, S contains
![]() $\kappa (S_1 \times S_2)$
in order for equality to hold in the dimension count.
$\kappa (S_1 \times S_2)$
in order for equality to hold in the dimension count.
There is an analogous result for the other boundary components, which we do not need in this paper. In this case, we say S degenerates to
![]() $\Xi ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
if S intersects
$\Xi ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
if S intersects
![]() $\lambda ({\overline {{\mathcal T}}}^{f_1}_{(r_1,s_1);1} \times \tilde {\mathcal T}^{f_2}_{(r_2,s_2);1})$
. In this case, we allow
$\lambda ({\overline {{\mathcal T}}}^{f_1}_{(r_1,s_1);1} \times \tilde {\mathcal T}^{f_2}_{(r_2,s_2);1})$
. In this case, we allow
![]() $(r_1,s_1)=(0,0)$
to be a valid trielliptic signature, and require that
$(r_1,s_1)=(0,0)$
to be a valid trielliptic signature, and require that
![]() $r_1+r_2=r-1$
and
$r_1+r_2=r-1$
and
![]() $s_1+s_2=s-1$
, and
$s_1+s_2=s-1$
, and
![]() $f_1 + f_2 \leq f-2$
.
$f_1 + f_2 \leq f-2$
.
Proposition 6.3. Suppose S has a balanced degeneration to
![]() $\Xi ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
. For
$\Xi ((r_1,s_1)^{f_1}, (r_2, s_2)^{f_2})$
. For
![]() $i=1,2$
, suppose (7) is true. Then
$i=1,2$
, suppose (7) is true. Then
![]() $\dim (S)= s-1 +f/2$
and S contains
$\dim (S)= s-1 +f/2$
and S contains
![]() $\lambda (S_1 \times S_2)$
, where
$\lambda (S_1 \times S_2)$
, where
![]() $S_i$
denotes a component of
$S_i$
denotes a component of
![]() ${\overline {{\mathcal T}}}^{f_i}_{(r_i,s_i);1}$
for
${\overline {{\mathcal T}}}^{f_i}_{(r_i,s_i);1}$
for
![]() $i=1,2$
.
$i=1,2$
.
Proof. The proof is almost the same as for Proposition 6.2. For a
![]() $\Xi $
-degeneration, recall that
$\Xi $
-degeneration, recall that
![]() $s_1+s_2=s-1$
,
$s_1+s_2=s-1$
,
![]() $r_1+r_2=r-1$
, and
$r_1+r_2=r-1$
, and
![]() $f_1+f_2 \leq f-2$
. Marking an orbit increases the dimension by 1, so
$f_1+f_2 \leq f-2$
. Marking an orbit increases the dimension by 1, so
![]() $\mathrm {dim}({\overline {{\mathcal T}}}^{f_1}_{(r_1,s_1);1})=s_i+f_i/2$
. Then
$\mathrm {dim}({\overline {{\mathcal T}}}^{f_1}_{(r_1,s_1);1})=s_i+f_i/2$
. Then
so
6.2 A partial generalization of Proposition 5.9
When
![]() $f=B(r,s)-2$
, then the p-rank f stratum has codimension
$f=B(r,s)-2$
, then the p-rank f stratum has codimension
![]() $1$
in
$1$
in
![]() ${\mathcal T}_{(r,s)}$
, by Proposition 5.9. When
${\mathcal T}_{(r,s)}$
, by Proposition 5.9. When
![]() $p \equiv 2 \bmod 3$
is odd, by Theorem 5.11,
$p \equiv 2 \bmod 3$
is odd, by Theorem 5.11,
![]() ${\mathcal T}_{(r,s)}^f$
is non-empty for each
${\mathcal T}_{(r,s)}^f$
is non-empty for each
![]() $0 \leq f \leq 2\mathrm {min}\{r,s\}$
with f even.
$0 \leq f \leq 2\mathrm {min}\{r,s\}$
with f even.
When
![]() $p \equiv 2 \bmod 3$
is odd, we would like to generalize Proposition 5.9 by showing that every component of the p-rank
$p \equiv 2 \bmod 3$
is odd, we would like to generalize Proposition 5.9 by showing that every component of the p-rank
![]() $f=B(r,s)-4$
stratum has codimension
$f=B(r,s)-4$
stratum has codimension
![]() $2$
in
$2$
in
![]() ${\mathcal T}_{(r,s)}$
. One reason this is hard to show is because it is not known whether the p-rank strata are nested in each other; specifically, it is not known whether every component of the
${\mathcal T}_{(r,s)}$
. One reason this is hard to show is because it is not known whether the p-rank strata are nested in each other; specifically, it is not known whether every component of the
![]() $f=B(r,s)-4$
stratum is contained in the closure of the
$f=B(r,s)-4$
stratum is contained in the closure of the
![]() $f=B(r,s)-2$
stratum.
$f=B(r,s)-2$
stratum.
In the next result, we are able to extend Proposition 5.9 in this desired way but only under the strong restriction that
![]() $\mathrm {min}\{r,s\}=2$
.
$\mathrm {min}\{r,s\}=2$
.
Corollary 6.4. Let
![]() $p \equiv 2 \bmod 3$
be odd. Let
$p \equiv 2 \bmod 3$
be odd. Let
![]() $(r,s)$
be a trielliptic signature with
$(r,s)$
be a trielliptic signature with
![]() $\mathrm {min}\{r,s\}=2$
. Let
$\mathrm {min}\{r,s\}=2$
. Let
![]() $f=0$
. If
$f=0$
. If
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(r,s)}^0$
, then
${\overline {{\mathcal T}}}_{(r,s)}^0$
, then
![]() $\dim ({\mathcal S}) = \max \{r,s\}-1$
.
$\dim ({\mathcal S}) = \max \{r,s\}-1$
.
In the rest of the section, we prove Corollary 6.4. By symmetry, it suffices to suppose
![]() $r=2$
; then
$r=2$
; then
![]() $s=2,3,4,5$
, and we handle these cases separately.
$s=2,3,4,5$
, and we handle these cases separately.
Corollary 6.4 is an application of Theorem 4.3, which we restate in the trielliptic context: suppose
![]() ${\mathcal S}$
is an irreducible component of the p-rank
${\mathcal S}$
is an irreducible component of the p-rank
![]() $0$
stratum
$0$
stratum
![]() ${\overline {{\mathcal T}}}_{(r,s)}^0$
of
${\overline {{\mathcal T}}}_{(r,s)}^0$
of
![]() ${\overline {{\mathcal T}}}_{(r,s)}$
; let
${\overline {{\mathcal T}}}_{(r,s)}$
; let
![]() $\sigma = \mathrm {dim}({\mathcal S})$
; then there exists
$\sigma = \mathrm {dim}({\mathcal S})$
; then there exists
![]() $\eta \in {\mathcal S}$
such that the curve
$\eta \in {\mathcal S}$
such that the curve
![]() $Y_\eta $
of compact type represented by
$Y_\eta $
of compact type represented by
![]() $\eta $
is reducible, with at least
$\eta $
is reducible, with at least
![]() $\sigma + 1$
components, such that the
$\sigma + 1$
components, such that the
![]() $\mathbb {Z}/3 \mathbb {Z}$
-action stabilizes and acts nontrivially on each component.
$\mathbb {Z}/3 \mathbb {Z}$
-action stabilizes and acts nontrivially on each component.
6.2.1 The case
 $r=2$
and
$r=2$
and
 $s=3$
$s=3$
Lemma 6.5. If S is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(2,3)}^0$
, then
${\overline {{\mathcal T}}}_{(2,3)}^0$
, then
![]() $\dim (S)=2$
.
$\dim (S)=2$
.
Proof. When the signature is
![]() $(2,3)$
, the inertia type is
$(2,3)$
, the inertia type is
![]() ${\overline {\gamma }}=(1,1,2,2,2,2,2)$
.
${\overline {\gamma }}=(1,1,2,2,2,2,2)$
.
By Theorem 5.5,
![]() $\dim (S) \geq 2$
. Since
$\dim (S) \geq 2$
. Since
![]() ${\mathcal T}_{(2,3)}$
is affine, S intersects either
${\mathcal T}_{(2,3)}$
is affine, S intersects either
![]() $\Delta _1=\Delta _4$
or
$\Delta _1=\Delta _4$
or
![]() $\Delta _2=\Delta _3$
. If S intersects
$\Delta _2=\Delta _3$
. If S intersects
![]() $\Delta _2$
, then S has a balanced degeneration to
$\Delta _2$
, then S has a balanced degeneration to
![]() $\Delta ((1,1)^0, (1,2)^0)$
. By Lemma 5.7, the hypothesis in (7) is true and so
$\Delta ((1,1)^0, (1,2)^0)$
. By Lemma 5.7, the hypothesis in (7) is true and so
![]() $\dim (S)=2$
by Proposition 6.2.
$\dim (S)=2$
by Proposition 6.2.
We assume that S does not intersect
![]() $\Delta _2$
and that
$\Delta _2$
and that
![]() $\dim (S) \geq 3$
and find a contradiction. By Theorem 4.3, S contains a point
$\dim (S) \geq 3$
and find a contradiction. By Theorem 4.3, S contains a point
![]() $\eta $
representing a curve
$\eta $
representing a curve
![]() $Y_\eta $
with at least four components. Since
$Y_\eta $
with at least four components. Since
![]() $Y_\eta $
has genus
$Y_\eta $
has genus
![]() $5$
, it has three components of genus
$5$
, it has three components of genus
![]() $1$
and one component
$1$
and one component
![]() $Y_0$
of genus
$Y_0$
of genus
![]() $2$
(which is possibly reducible).
$2$
(which is possibly reducible).
In the dual graph of
![]() $Y_\eta $
, we replace the vertex representing
$Y_\eta $
, we replace the vertex representing
![]() $Y_0$
by two vertices connected by a marked edge. This is illustrated in Figure 1: the schematic represents the four components of the curve, with the branch points marked by their canonical generators of inertia (the admissible condition implies that the two canonical generators of inertia are inverses at each ordinary double point); the schematic in Figure 2 represents the dual graph of Y.
$Y_0$
by two vertices connected by a marked edge. This is illustrated in Figure 1: the schematic represents the four components of the curve, with the branch points marked by their canonical generators of inertia (the admissible condition implies that the two canonical generators of inertia are inverses at each ordinary double point); the schematic in Figure 2 represents the dual graph of Y.

Figure 1 Picture of the singular curve
![]() $Y_\eta $
$Y_\eta $

Figure 2 The dual graph of
![]() $Y_\eta $
$Y_\eta $
The moduli point of Y is in
![]() $\kappa (\tilde {\mathcal T}^0_{(1,0)} \times \tilde {\mathcal T}^0_{(1,3)})$
, but this is not a balanced degeneration. Note that
$\kappa (\tilde {\mathcal T}^0_{(1,0)} \times \tilde {\mathcal T}^0_{(1,3)})$
, but this is not a balanced degeneration. Note that
![]() $\mathrm {dim}(\tilde {\mathcal T}^0_{(1,0)})=0$
and
$\mathrm {dim}(\tilde {\mathcal T}^0_{(1,0)})=0$
and
![]() $\mathrm {dim}(\tilde {\mathcal T}^0_{(1,3)})=2$
by Lemma 5.7.
$\mathrm {dim}(\tilde {\mathcal T}^0_{(1,3)})=2$
by Lemma 5.7.
By Proposition 3.3,
![]() $\mathrm {dim}(S) \leq 3$
. If
$\mathrm {dim}(S) \leq 3$
. If
![]() $\mathrm {dim}(S) = 2$
, the proof is complete. If
$\mathrm {dim}(S) = 2$
, the proof is complete. If
![]() $\mathrm {dim}(S) =3$
, then there is a component
$\mathrm {dim}(S) =3$
, then there is a component
![]() $S_1$
of
$S_1$
of
![]() $\tilde {\mathcal T}^0_{(1,0)}$
and a component
$\tilde {\mathcal T}^0_{(1,0)}$
and a component
![]() $S_2$
of
$S_2$
of
![]() $\tilde {\mathcal T}^0_{(1,3)}$
such that S contains
$\tilde {\mathcal T}^0_{(1,3)}$
such that S contains
![]() $\kappa (S_1 \times S_2)$
.
$\kappa (S_1 \times S_2)$
.
Consider the unitary Shimura variety
![]() $\mathrm {Sh}$
attached to the data of
$\mathrm {Sh}$
attached to the data of
![]() $\ell =3$
and the signature type
$\ell =3$
and the signature type
![]() $(1,3)$
; let
$(1,3)$
; let
![]() $\Sigma $
be the irreducible component of
$\Sigma $
be the irreducible component of
![]() $\mathrm {Sh}$
which contains the Torelli locus; and let
$\mathrm {Sh}$
which contains the Torelli locus; and let
![]() $\Sigma ^0$
denote the p-rank
$\Sigma ^0$
denote the p-rank
![]() $0$
stratum of
$0$
stratum of
![]() $\Sigma $
. By Proposition 5.8,
$\Sigma $
. By Proposition 5.8,
![]() $\Sigma ^0$
is irreducible.
$\Sigma ^0$
is irreducible.
Consider a (labeled) tree
![]() $\eta '$
of four elliptic curves (with dual graph in Figure 3); this is a singular trielliptic curve with signature type
$\eta '$
of four elliptic curves (with dual graph in Figure 3); this is a singular trielliptic curve with signature type
![]() $(1,3)$
and p-rank
$(1,3)$
and p-rank
![]() $0$
. Its Jacobian is represented by a point of
$0$
. Its Jacobian is represented by a point of
![]() $\Sigma ^0$
, and thus by a point in the closure of
$\Sigma ^0$
, and thus by a point in the closure of
![]() $S_2$
. This implies that the point
$S_2$
. This implies that the point
![]() $\kappa (S_1 \times \eta ')$
is in
$\kappa (S_1 \times \eta ')$
is in
![]() $\Delta _2[S]$
, which is a contradiction.
$\Delta _2[S]$
, which is a contradiction.

Figure 3 A point
![]() $\eta '$
of
$\eta '$
of
![]() ${\overline {{\mathcal T}}}^0_{1,3}$
${\overline {{\mathcal T}}}^0_{1,3}$
6.2.2 The case
 $r=2$
and
$r=2$
and
 $s=4$
$s=4$
Lemma 6.6. If S is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(2,4)}^0$
, then
${\overline {{\mathcal T}}}_{(2,4)}^0$
, then
![]() $\dim (S)=3$
.
$\dim (S)=3$
.
Proof. By Theorem 5.5,
![]() $\dim (S) \geq 3$
. Since
$\dim (S) \geq 3$
. Since
![]() ${\mathcal T}_{(2,4)}$
is affine, S intersects either
${\mathcal T}_{(2,4)}$
is affine, S intersects either
![]() $\Delta _1$
or
$\Delta _1$
or
![]() $\Delta _2$
or
$\Delta _2$
or
![]() $\Delta _3$
. Then S has a balanced degeneration to either
$\Delta _3$
. Then S has a balanced degeneration to either
![]() $\Delta ((0,1)^0, (2,3)^0)$
or
$\Delta ((0,1)^0, (2,3)^0)$
or
![]() $\Delta ((1,1)^0, (1,3)^0)$
or
$\Delta ((1,1)^0, (1,3)^0)$
or
![]() $\Delta ((1,2)^0, (1,2)^0)$
. The result follows from Proposition 6.2, with the hypothesis in (7) verified by Lemmas 5.7 and 6.5.
$\Delta ((1,2)^0, (1,2)^0)$
. The result follows from Proposition 6.2, with the hypothesis in (7) verified by Lemmas 5.7 and 6.5.
6.2.3 The case
 $(r,s)=(2,5)$
$(r,s)=(2,5)$
Lemma 6.7. If S is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(2,5)}^0$
, then
${\overline {{\mathcal T}}}_{(2,5)}^0$
, then
![]() $\dim (S)=4$
.
$\dim (S)=4$
.
Proof. By Theorem 5.5,
![]() $\dim (S) \geq 4$
. We assume
$\dim (S) \geq 4$
. We assume
![]() $\dim (S) \geq 5$
and find a contradiction. By Theorem 4.3, there exists a point
$\dim (S) \geq 5$
and find a contradiction. By Theorem 4.3, there exists a point
![]() $\eta \in S$
such that the curve
$\eta \in S$
such that the curve
![]() $Y=C_\eta $
has at least six components. Since Y has genus
$Y=C_\eta $
has at least six components. Since Y has genus
![]() $7$
, it has five components of genus
$7$
, it has five components of genus
![]() $1$
and one component of genus 2 (which is possibly reducible).
$1$
and one component of genus 2 (which is possibly reducible).
In the dual graph of Y, we replace the vertex representing the curve of genus
![]() $2$
by two vertices connected by a marked edge. One possibility for the dual graph is seen in Figure 4.
$2$
by two vertices connected by a marked edge. One possibility for the dual graph is seen in Figure 4.

Figure 4 The dual graph from the proof of Lemma 6.7.
Regardless of the location of the marked edge,
![]() $\eta $
is in
$\eta $
is in
![]() $\kappa (\tilde {\mathcal T}^0_{(1,2)} \times \tilde {\mathcal T}^0_{(1,3)})$
. Thus, S has a balanced degeneration to
$\kappa (\tilde {\mathcal T}^0_{(1,2)} \times \tilde {\mathcal T}^0_{(1,3)})$
. Thus, S has a balanced degeneration to
![]() $\Delta ((1,2)^0, (1,3)^0)$
. By Proposition 6.2(1),
$\Delta ((1,2)^0, (1,3)^0)$
. By Proposition 6.2(1),
![]() $\dim (S) \leq 4$
, which gives a contradiction. Hence,
$\dim (S) \leq 4$
, which gives a contradiction. Hence,
![]() $\dim (S) = 4$
.
$\dim (S) = 4$
.
6.2.4 The case
 $(r,s)=(2,2)$
$(r,s)=(2,2)$
The situation for the trielliptic signature
![]() $(2,2)$
is more complicated; as seen in Example 7.2,
$(2,2)$
is more complicated; as seen in Example 7.2,
![]() $\Delta _1[{\overline {{\mathcal T}}}^0_{2,2}]$
has dimension
$\Delta _1[{\overline {{\mathcal T}}}^0_{2,2}]$
has dimension
![]() $1$
, which is larger than expected. To avoid issues raised by problem, we use some results about the Shimura variety
$1$
, which is larger than expected. To avoid issues raised by problem, we use some results about the Shimura variety
![]() $\mathrm {Sh}$
attached to the data
$\mathrm {Sh}$
attached to the data
![]() $\ell =3$
and signature type
$\ell =3$
and signature type
![]() $(2,2)$
.
$(2,2)$
.
Lemma 6.8. If S is an irreducible component of
![]() ${\overline {{\mathcal T}}}^0_{(2,2)}$
, then
${\overline {{\mathcal T}}}^0_{(2,2)}$
, then
![]() $\dim (S)=1$
.
$\dim (S)=1$
.
Proof. If S intersects
![]() $\Delta _2$
, then S has a balanced degeneration to
$\Delta _2$
, then S has a balanced degeneration to
![]() $\Delta ((1,1)^0, (1, 1)^0)$
. Then
$\Delta ((1,1)^0, (1, 1)^0)$
. Then
![]() $\dim (S)=1$
by Proposition 6.2(1).
$\dim (S)=1$
by Proposition 6.2(1).
Suppose that S does not intersect
![]() $\Delta _2$
. Then S intersects
$\Delta _2$
. Then S intersects
![]() $\Delta _1$
and S degenerates to
$\Delta _1$
and S degenerates to
![]() $\Delta ((1,0)^0, (1, 2)^0)$
. Then
$\Delta ((1,0)^0, (1, 2)^0)$
. Then
![]() $\dim (S)=1$
or
$\dim (S)=1$
or
![]() $\dim (S)=2$
by Proposition 6.2(2).
$\dim (S)=2$
by Proposition 6.2(2).
Assume
![]() $\dim (S) =2$
. Under this assumption, we prove that S intersects
$\dim (S) =2$
. Under this assumption, we prove that S intersects
![]() $\Delta _2$
, which gives a contradiction. By Theorem 4.3, S contains a point
$\Delta _2$
, which gives a contradiction. By Theorem 4.3, S contains a point
![]() $\eta $
representing a trielliptic curve
$\eta $
representing a trielliptic curve
![]() $C_\eta $
of compact type with at least three components. Then
$C_\eta $
of compact type with at least three components. Then
![]() $C_{\eta }$
has one irreducible component of genus 2 with two elliptic tails, since S does not intersect
$C_{\eta }$
has one irreducible component of genus 2 with two elliptic tails, since S does not intersect
![]() $\Delta _2$
.
$\Delta _2$
.
Consider the Shimura variety
![]() $\mathrm {Sh}$
attached to the data
$\mathrm {Sh}$
attached to the data
![]() $\ell =3$
and signature type
$\ell =3$
and signature type
![]() $(2,2)$
. Let
$(2,2)$
. Let
![]() $\Sigma $
be the irreducible component of
$\Sigma $
be the irreducible component of
![]() $\mathrm {Sh}$
containing the image of the Torelli locus. Let
$\mathrm {Sh}$
containing the image of the Torelli locus. Let
![]() $S'$
be the image of S under the embedding
$S'$
be the image of S under the embedding
![]() ${\overline {{\mathcal T}}}^0_{2,2} \to \Sigma $
. Then
${\overline {{\mathcal T}}}^0_{2,2} \to \Sigma $
. Then
![]() $S'$
is contained in the supersingular locus N of
$S'$
is contained in the supersingular locus N of
![]() $\Sigma $
. Each of the supersingular components of
$\Sigma $
. Each of the supersingular components of
![]() $\Sigma $
has dimension
$\Sigma $
has dimension
![]() $2$
by [Reference Howard and Pappas12, Th. B]. It follows that
$2$
by [Reference Howard and Pappas12, Th. B]. It follows that
![]() $S'$
is a component of N. By [Reference Howard and Pappas12, Th. 3.12], every component of N contains a point
$S'$
is a component of N. By [Reference Howard and Pappas12, Th. 3.12], every component of N contains a point
![]() $\xi $
where N intersects another component of N. The point
$\xi $
where N intersects another component of N. The point
![]() $\xi $
parameterizes an abelian variety A which decomposes, together with the polarization, into a direct sum of the form
$\xi $
parameterizes an abelian variety A which decomposes, together with the polarization, into a direct sum of the form
![]() $A_1 \oplus A_2$
where
$A_1 \oplus A_2$
where
![]() $\mathrm {dim}(A_i)=2$
and
$\mathrm {dim}(A_i)=2$
and
![]() $\mathbb {Z}[\zeta _3] \subset \mathrm {End}(A_i)$
. Then A is the Jacobian of a curve in
$\mathbb {Z}[\zeta _3] \subset \mathrm {End}(A_i)$
. Then A is the Jacobian of a curve in
![]() $\Delta _2[{\overline {{\mathcal T}}}^0_{2,2}]$
, which gives a contradiction.
$\Delta _2[{\overline {{\mathcal T}}}^0_{2,2}]$
, which gives a contradiction.
7 Concluding remarks
In Section 7.1, we complete the proof of the base case used in some results in the paper, such as Proposition 5.9. In the remaining sections, we explain some of the reasons why Theorem 5.11 is hard to generalize.
7.1 A computational approach to the base case
In this section, we prove that
![]() ${\mathcal T}^0_{(1,1)}$
is non-empty when
${\mathcal T}^0_{(1,1)}$
is non-empty when
![]() $p \equiv 2 \bmod 3$
is odd; this completes the proof of Lemma 5.7(1).
$p \equiv 2 \bmod 3$
is odd; this completes the proof of Lemma 5.7(1).
Suppose
![]() $\psi :Y \to {\mathbb P}^1$
is a
$\psi :Y \to {\mathbb P}^1$
is a
![]() $\mathbb {Z}/\ell \mathbb {Z}$
-cover. In [Reference Elkin9, §§2 and 3], Elkin determines formulas for the action of the Cartier operator
$\mathbb {Z}/\ell \mathbb {Z}$
-cover. In [Reference Elkin9, §§2 and 3], Elkin determines formulas for the action of the Cartier operator
![]() $\mathbf {C}$
on
$\mathbf {C}$
on
![]() $H^0(Y, \Omega ^1)$
. The Cartier operator is a semi-linear operator, and the p-rank is the rank of its gth iterate. For small
$H^0(Y, \Omega ^1)$
. The Cartier operator is a semi-linear operator, and the p-rank is the rank of its gth iterate. For small
![]() $\ell $
, g, and p, it is possible to compute the p-rank from Elkin’s work. We note that there are several choices involved in setting up the computation of iterates of the Cartier operator; these have led to mistakes in the literature, and the reader is advised to consult [Reference Achter and Howe2] to avoid repeating these.
$\ell $
, g, and p, it is possible to compute the p-rank from Elkin’s work. We note that there are several choices involved in setting up the computation of iterates of the Cartier operator; these have led to mistakes in the literature, and the reader is advised to consult [Reference Achter and Howe2] to avoid repeating these.
We restrict to the case that
![]() $\ell =3$
. Without loss of generality, we can suppose that
$\ell =3$
. Without loss of generality, we can suppose that
![]() $\psi $
is not branched above
$\psi $
is not branched above
![]() $\infty $
. As in (6), there is an equation
$\infty $
. As in (6), there is an equation
![]() $y^3 = p_1(x)p_2(x)^2$
for
$y^3 = p_1(x)p_2(x)^2$
for
![]() $\psi $
, where
$\psi $
, where
![]() $p_1(x), p_2(x) \in k[x]$
are square-free, monic, and relatively prime. Let
$p_1(x), p_2(x) \in k[x]$
are square-free, monic, and relatively prime. Let
![]() $d_1=\mathrm {deg}(p_1(x))$
and
$d_1=\mathrm {deg}(p_1(x))$
and
![]() $d_2=\mathrm {deg}(p_2(x))$
. From Lemma 5.3, recall that the trielliptic signature for
$d_2=\mathrm {deg}(p_2(x))$
. From Lemma 5.3, recall that the trielliptic signature for
![]() $\psi $
is given by
$\psi $
is given by
![]() $(r,s)$
where
$(r,s)$
where
![]() $r=(2d_1+d_2-3)/3$
and
$r=(2d_1+d_2-3)/3$
and
![]() $s = (d_1+2d_2-3)/3$
. Moreover,
$s = (d_1+2d_2-3)/3$
. Moreover,
![]() $g=d_1+d_2 - 2$
.
$g=d_1+d_2 - 2$
.
We restrict to the case
![]() $(r,s)=(1,1)$
and
$(r,s)=(1,1)$
and
![]() $g=2$
. Then
$g=2$
. Then
![]() $H^0(Y, \Omega ^1) = \mathcal {L}_1 \oplus \mathcal {L}_2$
where
$H^0(Y, \Omega ^1) = \mathcal {L}_1 \oplus \mathcal {L}_2$
where
We suppose that
![]() $p \equiv 2 \bmod 3$
; then the Cartier operator
$p \equiv 2 \bmod 3$
; then the Cartier operator
![]() $\mathbf {C}$
permutes
$\mathbf {C}$
permutes
![]() $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
![]() $\mathcal {L}_2$
.
$\mathcal {L}_2$
.
Let
![]() $e_1=(2p-1)/3$
and
$e_1=(2p-1)/3$
and
![]() $e_2 = (p-2)/3$
. Note that
$e_2 = (p-2)/3$
. Note that
![]() $e_1+e_2=p-1$
. Let
$e_1+e_2=p-1$
. Let
When
![]() $r=s=1$
, then
$r=s=1$
, then
![]() $\mathrm {deg}(h_1(x)) = \mathrm {deg}(h_2(x)) = 2p-2$
. In this case, for
$\mathrm {deg}(h_1(x)) = \mathrm {deg}(h_2(x)) = 2p-2$
. In this case, for
![]() $i=1,2$
, there is only one monomial
$i=1,2$
, there is only one monomial
![]() $x^e$
in
$x^e$
in
![]() $h_i(x)$
such that
$h_i(x)$
such that
![]() $e \equiv -1 \bmod p$
; let
$e \equiv -1 \bmod p$
; let
![]() $A_i$
be the coefficient of
$A_i$
be the coefficient of
![]() $x^{p-1}$
in
$x^{p-1}$
in
![]() $h_i(x)$
. By a special case of [Reference Elkin9, Th. 3.4],
$h_i(x)$
. By a special case of [Reference Elkin9, Th. 3.4],
Lemma 7.1.
-
1. If
 $p \equiv 2 \bmod 3$
is odd, then
$p \equiv 2 \bmod 3$
is odd, then
 ${\mathcal T}^0_{(1,1)}$
is non-empty: there exists a smooth trielliptic curve Y over
${\mathcal T}^0_{(1,1)}$
is non-empty: there exists a smooth trielliptic curve Y over
 $\overline {\mathbb {F}}_p$
with genus
$\overline {\mathbb {F}}_p$
with genus
 $2$
and p-rank
$2$
and p-rank
 $0$
.
$0$
. -
2. If
 $p=2$
, then
$p=2$
, then
 ${\mathcal T}^0_{(1,1)}$
is empty: there does not exist a smooth trielliptic curve Y over
${\mathcal T}^0_{(1,1)}$
is empty: there does not exist a smooth trielliptic curve Y over
 $\overline {\mathbb {F}}_2$
with genus
$\overline {\mathbb {F}}_2$
with genus
 $2$
and
$2$
and
 $2$
-rank
$2$
-rank
 $0$
.
$0$
.
Proof.
-
1. Let
 $p_1(x)=x^2-1$
and
$p_1(x)=x^2-1$
and
 $p_2(x)=x^2+1$
. We compute that By (8),
$p_2(x)=x^2+1$
. We compute that By (8), $$ \begin{align*} h_1(x) & = (x^2-1)^{e_1}(x^2+1)^{e_2} \\ & = \left(\sum_{j=0}^{e_1} (-1)^{e_1 -j}\dbinom{e_1}{j} x^{2j} \right) \left(\sum_{i=0}^{e_2} \dbinom{e_2}{i} x^{2i} \right). \end{align*} $$
$$ \begin{align*} h_1(x) & = (x^2-1)^{e_1}(x^2+1)^{e_2} \\ & = \left(\sum_{j=0}^{e_1} (-1)^{e_1 -j}\dbinom{e_1}{j} x^{2j} \right) \left(\sum_{i=0}^{e_2} \dbinom{e_2}{i} x^{2i} \right). \end{align*} $$
 $\mathbf {C}(\omega _{1,1})= A_1 \omega _{2,1}$
where
$\mathbf {C}(\omega _{1,1})= A_1 \omega _{2,1}$
where
 $A_1$
is the coefficient of
$A_1$
is the coefficient of
 $x^{p-1}$
in
$x^{p-1}$
in
 $h_1(x)$
. A pair
$h_1(x)$
. A pair
 $(i,j)$
contributes to this coefficient exactly when
$(i,j)$
contributes to this coefficient exactly when
 $2i+2j=p-1$
, or
$2i+2j=p-1$
, or
 $j=(p-1)/2 -i$
. Thus, The sum has an even number of terms. One can check that the ith and
$j=(p-1)/2 -i$
. Thus, The sum has an even number of terms. One can check that the ith and $$\begin{align*}A_1= \sum \limits_{i=0}^{e_2} (-1)^{\frac{p+1}{6}+i}\dbinom{e_1}{\frac{p-1}{2}-i}\dbinom{e_2}{i} .\end{align*}$$
$$\begin{align*}A_1= \sum \limits_{i=0}^{e_2} (-1)^{\frac{p+1}{6}+i}\dbinom{e_1}{\frac{p-1}{2}-i}\dbinom{e_2}{i} .\end{align*}$$
 $(e_2-i)$
th terms cancel, because
$(e_2-i)$
th terms cancel, because
 $((p-1)/2 -i)+((p-1)/2 - (e_2-i))=e_1$
and because i and
$((p-1)/2 -i)+((p-1)/2 - (e_2-i))=e_1$
and because i and
 $e_2-i$
have opposite parities. Thus,
$e_2-i$
have opposite parities. Thus,
 $A_1=0$
.The same argument, with the roles of
$A_1=0$
.The same argument, with the roles of
 $e_1$
and
$e_1$
and
 $e_2$
switched, shows that
$e_2$
switched, shows that
 $A_2=0$
. Thus,
$A_2=0$
. Thus,
 $\mathbf {C}$
is the zero operator (implying that Y is superspecial) and so Y has p-rank
$\mathbf {C}$
is the zero operator (implying that Y is superspecial) and so Y has p-rank
 $0$
.
$0$
.
-
2. Let
 $p=2$
. After an automorphism of
$p=2$
. After an automorphism of
 ${\mathbb P}^1$
, one can suppose that
${\mathbb P}^1$
, one can suppose that
 $p_1(x)=x^2+x+1$
and
$p_1(x)=x^2+x+1$
and
 $p_2(x)=(x-1)(x-a)$
for some
$p_2(x)=(x-1)(x-a)$
for some
 $a \in {\overline {\mathbb {F}}}_2$
. Then
$a \in {\overline {\mathbb {F}}}_2$
. Then
 $h_1(x)=p_1(x)$
and
$h_1(x)=p_1(x)$
and
 $h_2(x)=p_2(x)$
, so
$h_2(x)=p_2(x)$
, so
 $A_1=1$
and
$A_1=1$
and
 $A_2=-(a+1)$
. The determinant of the matrix of
$A_2=-(a+1)$
. The determinant of the matrix of
 $\mathbf {C}$
is
$\mathbf {C}$
is
 $a+1$
. If Y has
$a+1$
. If Y has
 $2$
-rank
$2$
-rank
 $0$
, then this determinant is zero, so
$0$
, then this determinant is zero, so
 $a \equiv 1 \bmod 2$
. Then
$a \equiv 1 \bmod 2$
. Then
 $p_2(x)$
is not square-free, so Y is singular.
$p_2(x)$
is not square-free, so Y is singular.
Elkin provides similar formulas for any prime degree
![]() $\ell $
and inertia type
$\ell $
and inertia type
![]() ${\overline {\gamma }}$
; unfortunately, this does not provide a viable way to study the p-rank strata when
${\overline {\gamma }}$
; unfortunately, this does not provide a viable way to study the p-rank strata when
![]() $g> 2$
and p is large for any
$g> 2$
and p is large for any
![]() $\ell $
, because the equations are algebraically complicated.
$\ell $
, because the equations are algebraically complicated.
7.2 Possibility of components fully contained in the boundary
Here is an important fact about the p-rank stratification of the hyperelliptic locus. When p is odd, the generic geometric point of each irreducible component of
![]() ${\overline {{\mathcal H}}}^f_g$
represents a smooth hyperelliptic curve, by [Reference Achter and Pries5, Lem. 3.1].
${\overline {{\mathcal H}}}^f_g$
represents a smooth hyperelliptic curve, by [Reference Achter and Pries5, Lem. 3.1].
The analogue of this fact is not true in general for the trielliptic locus. For example, when
![]() $p=2$
, then every point of
$p=2$
, then every point of
![]() ${\overline {{\mathcal T}}}^0_{(1,1)}$
represents a singular trielliptic curve by Lemma 7.1(2). This is the key reason for the restriction that p is odd in Proposition 5.9 and Theorem 5.11.
${\overline {{\mathcal T}}}^0_{(1,1)}$
represents a singular trielliptic curve by Lemma 7.1(2). This is the key reason for the restriction that p is odd in Proposition 5.9 and Theorem 5.11.
We give some other examples where this type of problem may occur.
Example 7.2. Let
![]() $p \equiv 2 \bmod 3$
be odd. Let
$p \equiv 2 \bmod 3$
be odd. Let
![]() $r=s=2$
and
$r=s=2$
and
![]() $f=0$
. Suppose
$f=0$
. Suppose
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^0$
. By Proposition 5.5,
${\overline {{\mathcal T}}}_{(2,2)}^0$
. By Proposition 5.5,
![]() $\mathrm {dim}({\mathcal S}) \geq 1$
.
$\mathrm {dim}({\mathcal S}) \geq 1$
.
Every component
![]() ${\widetilde {S}}_1$
of
${\widetilde {S}}_1$
of
![]() ${\widetilde {{\mathcal T}}}_{(1,0)}^0$
has dimension
${\widetilde {{\mathcal T}}}_{(1,0)}^0$
has dimension
![]() $0$
, and every component
$0$
, and every component
![]() ${\widetilde {S}}_2$
of
${\widetilde {S}}_2$
of
![]() ${\widetilde {{\mathcal T}}}_{(1,2)}^0$
has dimension
${\widetilde {{\mathcal T}}}_{(1,2)}^0$
has dimension
![]() $1$
. This means that
$1$
. This means that
![]() $\Delta _1[{\overline {{\mathcal T}}}_{(2,2)}^0]$
contains a component
$\Delta _1[{\overline {{\mathcal T}}}_{(2,2)}^0]$
contains a component
![]() $\kappa _{1,3}({\widetilde {S}}_1 \times {\widetilde {S}}_2)$
of dimension
$\kappa _{1,3}({\widetilde {S}}_1 \times {\widetilde {S}}_2)$
of dimension
![]() $1$
. In other words, there is a component
$1$
. In other words, there is a component
![]() ${\mathcal S}$
of
${\mathcal S}$
of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^0$
which has one of the following two problems: either
${\overline {{\mathcal T}}}_{(2,2)}^0$
which has one of the following two problems: either
![]() $\mathrm {dim}({\mathcal S})> 1$
(bigger than expected) or the generic point of
$\mathrm {dim}({\mathcal S})> 1$
(bigger than expected) or the generic point of
![]() ${\mathcal S}$
is contained in the boundary of
${\mathcal S}$
is contained in the boundary of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^0$
.
${\overline {{\mathcal T}}}_{(2,2)}^0$
.
The reason for the problem in Example 7.2 is that the pair
![]() $(1,0)$
and
$(1,0)$
and
![]() $(1,2)$
is not balanced, as in Definition 6.1. The inductive step for producing smooth trielliptic curves of larger genus and given p-rank works only when the pair of signatures is balanced.
$(1,2)$
is not balanced, as in Definition 6.1. The inductive step for producing smooth trielliptic curves of larger genus and given p-rank works only when the pair of signatures is balanced.
More generally, the problem seen in Example 7.2 arises when
![]() $p \equiv 2 \bmod 3$
is odd if
$p \equiv 2 \bmod 3$
is odd if
![]() $r \leq s \leq 2r-1$
and
$r \leq s \leq 2r-1$
and
![]() $f \leq 2r-2$
and when
$f \leq 2r-2$
and when
![]() $p=2$
if
$p=2$
if
![]() $3 \leq r \leq s \leq 2r -2$
.
$3 \leq r \leq s \leq 2r -2$
.
Example 7.3. Let
![]() $p \equiv 1 \bmod 3$
. Let
$p \equiv 1 \bmod 3$
. Let
![]() $r=s=2$
and
$r=s=2$
and
![]() $f=1$
. Suppose
$f=1$
. Suppose
![]() ${\mathcal S}$
is an irreducible component of
${\mathcal S}$
is an irreducible component of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^1$
. By Proposition 5.5,
${\overline {{\mathcal T}}}_{(2,2)}^1$
. By Proposition 5.5,
![]() $\mathrm {dim}({\mathcal S}) \geq 1$
.
$\mathrm {dim}({\mathcal S}) \geq 1$
.
Every component
![]() ${\widetilde {S}}_1$
of
${\widetilde {S}}_1$
of
![]() ${\widetilde {{\mathcal T}}}_{(1,1)}^0$
has dimension
${\widetilde {{\mathcal T}}}_{(1,1)}^0$
has dimension
![]() $0$
, and every component
$0$
, and every component
![]() ${\widetilde {S}}_2$
of
${\widetilde {S}}_2$
of
![]() ${\widetilde {{\mathcal T}}}_{(1,1)}^1$
has dimension
${\widetilde {{\mathcal T}}}_{(1,1)}^1$
has dimension
![]() $1$
. This means that
$1$
. This means that
![]() $\Delta _1[{\overline {{\mathcal T}}}_{(2,2)}^1]$
contains a component
$\Delta _1[{\overline {{\mathcal T}}}_{(2,2)}^1]$
contains a component
![]() $\kappa _{2,2}({\widetilde {S}}_1 \times {\widetilde {S}}_2)$
of dimension
$\kappa _{2,2}({\widetilde {S}}_1 \times {\widetilde {S}}_2)$
of dimension
![]() $1$
. In other words, there is a component
$1$
. In other words, there is a component
![]() ${\mathcal S}$
of
${\mathcal S}$
of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^1$
which has one of the following two problems: either
${\overline {{\mathcal T}}}_{(2,2)}^1$
which has one of the following two problems: either
![]() $\mathrm {dim}({\mathcal S})> 1$
(bigger than expected) or the generic point of
$\mathrm {dim}({\mathcal S})> 1$
(bigger than expected) or the generic point of
![]() ${\mathcal S}$
is contained in the boundary of
${\mathcal S}$
is contained in the boundary of
![]() ${\overline {{\mathcal T}}}_{(2,2)}^1$
.
${\overline {{\mathcal T}}}_{(2,2)}^1$
.
7.3 The wild case
 $p=3$
$p=3$
We include the case of trielliptic covers when
![]() $p=3$
.
$p=3$
.
Proposition 7.4. Suppose
![]() $k=\overline {{\mathbb F}}_3$
. Then there exists a
$k=\overline {{\mathbb F}}_3$
. Then there exists a
![]() $\mathbb {Z}/3 \mathbb {Z}$
-cover of
$\mathbb {Z}/3 \mathbb {Z}$
-cover of
![]() ${\mathbb P}^1_k$
having genus g and
${\mathbb P}^1_k$
having genus g and
![]() $3$
-rank
$3$
-rank
![]() $0$
if and only if
$0$
if and only if
![]() $g \not \equiv 2 \bmod 3$
. For
$g \not \equiv 2 \bmod 3$
. For
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $1 \leq e \leq g/2$
, there exists a
$1 \leq e \leq g/2$
, there exists a
![]() $\mathbb {Z}/3 \mathbb {Z}$
-cover of
$\mathbb {Z}/3 \mathbb {Z}$
-cover of
![]() ${\mathbb P}^1_k$
having genus g and
${\mathbb P}^1_k$
having genus g and
![]() $3$
-rank
$3$
-rank
![]() $2e$
.
$2e$
.
Proof. Suppose
![]() $\phi :Y \to {\mathbb P}^1_k$
is a
$\phi :Y \to {\mathbb P}^1_k$
is a
![]() $\mathbb {Z}/3\mathbb {Z}$
-cover. Then
$\mathbb {Z}/3\mathbb {Z}$
-cover. Then
![]() $\phi $
is given by an Artin–Schreier equation of the form
$\phi $
is given by an Artin–Schreier equation of the form
![]() $y^3-y=f(x)$
for some
$y^3-y=f(x)$
for some
![]() $f(x) \in k(x)$
. Suppose
$f(x) \in k(x)$
. Suppose
![]() $\mathrm {div}_\infty (f(x))=\sum _{j=0}^{e} d_j P_j$
is the pole divisor of
$\mathrm {div}_\infty (f(x))=\sum _{j=0}^{e} d_j P_j$
is the pole divisor of
![]() $f(x)$
. By Artin–Schreier theory, one can suppose that
$f(x)$
. By Artin–Schreier theory, one can suppose that
![]() $3 \nmid d_j$
for each j. Let
$3 \nmid d_j$
for each j. Let
![]() $e_j=d_j+1$
.
$e_j=d_j+1$
.
The Riemann–Hurwitz formula and the Deuring–Shafarevich formula imply that the genus of Y is
![]() $g=-2+\sum _{j=0}^{e} e_j$
and the
$g=-2+\sum _{j=0}^{e} e_j$
and the
![]() $3$
-rank of Y is
$3$
-rank of Y is
![]() $2e$
[Reference Pries and Zhu21, Lem. 2.6]. Consider the
$2e$
[Reference Pries and Zhu21, Lem. 2.6]. Consider the
![]() $3$
-rank f strata
$3$
-rank f strata
![]() ${\mathcal A}_{g}^f$
of the moduli space of genus g Artin–Schreier covers of
${\mathcal A}_{g}^f$
of the moduli space of genus g Artin–Schreier covers of
![]() ${\mathbb P}^1_k$
. By [Reference Pries and Zhu21, Th. 1.1], the irreducible components of
${\mathbb P}^1_k$
. By [Reference Pries and Zhu21, Th. 1.1], the irreducible components of
![]() ${\mathcal A}_{g}^f$
are in bijection with partitions
${\mathcal A}_{g}^f$
are in bijection with partitions
![]() $\sum _{j=0}^{e} e_j$
of
$\sum _{j=0}^{e} e_j$
of
![]() $g+2$
such that
$g+2$
such that
![]() $e_j \not \equiv 1 \bmod 3$
and the dimension of the component is
$e_j \not \equiv 1 \bmod 3$
and the dimension of the component is
![]() $g-1-\sum _{j=0}^{e} \lfloor \frac {d_j}{3} \rfloor $
.
$g-1-\sum _{j=0}^{e} \lfloor \frac {d_j}{3} \rfloor $
.
Thus, when
![]() $p=3$
, there exists a
$p=3$
, there exists a
![]() $\mathbb {Z}/3\mathbb {Z}$
-cover of
$\mathbb {Z}/3\mathbb {Z}$
-cover of
![]() ${\mathbb P}^1_k$
having genus g and
${\mathbb P}^1_k$
having genus g and
![]() $3$
-rank
$3$
-rank
![]() $0$
if and only if
$0$
if and only if
![]() $g \not \equiv 2 \bmod 3$
. By an inductive argument, one can show: for
$g \not \equiv 2 \bmod 3$
. By an inductive argument, one can show: for
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $1 \leq e \leq g/2$
, there exists a partition
$1 \leq e \leq g/2$
, there exists a partition
![]() $\sum _{j=0}^r e_j$
of
$\sum _{j=0}^r e_j$
of
![]() $g+2$
into
$g+2$
into
![]() $r+1$
positive integers such that
$r+1$
positive integers such that
![]() $e_j \not \equiv 1 \bmod 3$
and thus there exists a
$e_j \not \equiv 1 \bmod 3$
and thus there exists a
![]() $\mathbb {Z}/3\mathbb {Z}$
-cover of
$\mathbb {Z}/3\mathbb {Z}$
-cover of
![]() ${\mathbb P}^1_k$
having genus g and
${\mathbb P}^1_k$
having genus g and
![]() $3$
-rank
$3$
-rank
![]() $2r$
.
$2r$
.
Acknowledgment
We thank the anonymous referees for helpful comments.