Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T00:04:55.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Conditions for the Heat Equation in a Several-Dimensional Region*

Published online by Cambridge University Press:  22 January 2016

G. Gallavotti  and
H. P. McKean
G. Gallavotti
Affiliation:
Universita di Roma, Roma, Italy, Courant Institute of Mathematical Sciences, New York University, New York, U.S.A.
H. P. McKean
Affiliation:
Universita di Roma, Roma, Italy, Courant Institute of Mathematical Sciences, New York University, New York, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

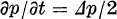The heat equation is to be solved in a severaldimensional region D with 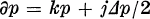on the boundary B of D. The elementary solution (Green’s function) is interpreted as the transition density of an associated Brownian motion. The latter is built up pathwise from the free Brownian motion by simple geometric and probabilistic transformations.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 47 , September 1972 , pp. 1 - 14
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

Footnotes

*

The work of the second author was supported in part by the Office of Naval Research, Contract N00014-67-A-0467-0014. Reproduction in whole or in part is permitted for any purpose of the United States Government.

References

[1] Bers, L., John, F., and Schechter, M., Partial Differential Equations, Interscience, New York, 1964.Google Scholar
[2] Fukushima, M., Boundary conditions for multi-dimensional Brownian motion with symmetric resolvent densities, J. Math. Soc. Japan, 21, 58–93 (1969).Google Scholar
[3] Itô, K., and McKean, H. P., Brownian motion on a half-line, Illinois J. Math., 7, 181–231 (1963).CrossRefGoogle Scholar
[4] Itô, K., and McKean, H. P., Diffusion Processes and their Sample Paths, J. Springer, Berlin, 1965.Google Scholar
[5] Levy, P., Processus Stochastiques et Mouvement Brownien, Gauthier-Villars, Paris, 1948.Google Scholar
[6] McKean, H. P., Stochastic Integrals, Academic Press, New York, 1969.Google Scholar
[7] Sommerfeld, A., Partial Differential Equations in Physics, Academic Press, New York, 1949.Google Scholar