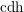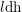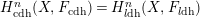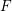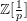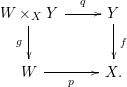1 Introduction
Context—motives of singular schemes (with compact support). In [Reference VoevodskyVoe00], Voevodsky constructed a triangulated category of motives
![]() $DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
using smooth schemes. In order to
$DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
using smooth schemes. In order to
∙ extend the motive functor
 $M:\mathsf{Sm}_{k}\rightarrow DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
from smooth
$M:\mathsf{Sm}_{k}\rightarrow DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
from smooth
 $k$
-schemes to all separated finite type
$k$
-schemes to all separated finite type
 $k$
-schemes, and
$k$
-schemes, and∙ have access to a well-defined theory of motives with compact support
 $M^{c}:\mathsf{Sch}_{k}^{\operatorname{prop}}\rightarrow DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
,
$M^{c}:\mathsf{Sch}_{k}^{\operatorname{prop}}\rightarrow DM_{\operatorname{gm}}^{\operatorname{eff}}(k)$
,
he proves a
![]() $\operatorname{cdh}$
-descent result. However, his proof only works in the presence of strong resolution of singularities (for example, in characteristic zero). In [Reference KellyKel17], the resolution of singularities assumption was removed, at least if one works with
$\operatorname{cdh}$
-descent result. However, his proof only works in the presence of strong resolution of singularities (for example, in characteristic zero). In [Reference KellyKel17], the resolution of singularities assumption was removed, at least if one works with
![]() $\mathbb{Z}[\frac{1}{p}]$
-coefficients, where
$\mathbb{Z}[\frac{1}{p}]$
-coefficients, where
![]() $p$
is the exponential characteristic of the base field. The proof in [Reference KellyKel17] has two main steps, namely [Reference KellyKel17, Corollary 2.5.4] and [Reference KellyKel17, Theorem 3.2.12]. This present article provides a shortcut to the first one. For more details about the strategy of [Reference KellyKel17] we recommend consulting [Reference KellyKel17, Chapter 1] and/or [Reference KellyKel17, Chapter 4].
$p$
is the exponential characteristic of the base field. The proof in [Reference KellyKel17] has two main steps, namely [Reference KellyKel17, Corollary 2.5.4] and [Reference KellyKel17, Theorem 3.2.12]. This present article provides a shortcut to the first one. For more details about the strategy of [Reference KellyKel17] we recommend consulting [Reference KellyKel17, Chapter 1] and/or [Reference KellyKel17, Chapter 4].
Main result. The main theorem of this article is:
Theorem 1. (cf. Theorem 30)
Suppose
![]() $S$
is a finite dimensional Noetherian separated scheme of positive characteristic
$S$
is a finite dimensional Noetherian separated scheme of positive characteristic
![]() $p\neq l$
,
$p\neq l$
,
![]() $\mathsf{Sch}_{S}$
the category of separated finite type
$\mathsf{Sch}_{S}$
the category of separated finite type
![]() $S$
-schemes, and
$S$
-schemes, and
![]() $F$
a presheaf of
$F$
a presheaf of
![]() $\mathbb{Z}_{(l)}$
-modules on
$\mathbb{Z}_{(l)}$
-modules on
![]() $\mathsf{Sch}_{S}$
satisfying all of:
$\mathsf{Sch}_{S}$
satisfying all of:
- (
 $\operatorname{uh}$
-invariance)
$\operatorname{uh}$
-invariance)  $F(X)\cong F(Y)$
for any universal homeomorphism
$F(X)\cong F(Y)$
for any universal homeomorphism
 $Y\rightarrow X$
.
$Y\rightarrow X$
.- (Traces)
 $F$
has covariant “trace” morphisms associated to finite flat surjective morphisms, see Definition 13.
$F$
has covariant “trace” morphisms associated to finite flat surjective morphisms, see Definition 13.- (G1)
 $F(R)\subseteq F(\operatorname{Frac}(R))$
for every finite rank Hensel valuation ringFootnote
1
$F(R)\subseteq F(\operatorname{Frac}(R))$
for every finite rank Hensel valuation ringFootnote
1
 $R$
.
$R$
.- (G2)
 $F(R)\rightarrow F(R/\mathfrak{p})$
is surjective for every finite rank Hensel valuation ring
$F(R)\rightarrow F(R/\mathfrak{p})$
is surjective for every finite rank Hensel valuation ring
 $R$
and prime
$R$
and prime
 $\mathfrak{p}\subset R$
.
$\mathfrak{p}\subset R$
.
Then the canonical comparison morphism is an isomorphism:
However, the main result of this article is its proof. The proof of [Reference KellyKel17, Corollary 2.5.4] is a poorly structured collection of lemmas, which are difficult to arrange into some kind global narrative, and the hypotheses of [Reference KellyKel17, Corollary 2.5.4] are an awkward list of very special properties that do not give much insight into why the cohomologies should agree.
The proof of Theorem 30 on the other hand, is shortFootnote
2
and linear, and one can mostly explain how its hypotheses are used in the proof:
![]() $\mathbb{Z}_{(l)}$
-linearity and traces are to give descent for finite-flat-surjective-prime-to-
$\mathbb{Z}_{(l)}$
-linearity and traces are to give descent for finite-flat-surjective-prime-to-
![]() $l$
morphisms (cf. Lemma 2), universal homeomorphism invariance is to correct non-Nagataness of Hensel valuation rings (cf. Lemma 3), and (G2) is to control
$l$
morphisms (cf. Lemma 2), universal homeomorphism invariance is to correct non-Nagataness of Hensel valuation rings (cf. Lemma 3), and (G2) is to control
![]() $\text{}\underline{H}_{l\operatorname{dh}}^{1}F$
(cf. Equation (2) on page 204). Unfortunately, (G1) remains a little mysterious. It is easy to say how it is used in the proof (it produces inclusions
$\text{}\underline{H}_{l\operatorname{dh}}^{1}F$
(cf. Equation (2) on page 204). Unfortunately, (G1) remains a little mysterious. It is easy to say how it is used in the proof (it produces inclusions
![]() $F(X)\subseteq F_{l\operatorname{dh}}(X)\subseteq \prod _{x\in X}F(x)$
, cf. Lemma 28, Proposition 29), but not why it should be a necessary ingredient. See also Remark 23 for more on this.
$F(X)\subseteq F_{l\operatorname{dh}}(X)\subseteq \prod _{x\in X}F(x)$
, cf. Lemma 28, Proposition 29), but not why it should be a necessary ingredient. See also Remark 23 for more on this.
The class of presheaves covered by the hypotheses of Theorem 30 is reasonably large. Any cohomology theory representable in the motivic stable homotopy category is invariant under universal homeomorphisms (at least with
![]() $\mathbb{Z}[\frac{1}{p}]$
-coefficients), [Reference Elmanto and KhanEK18], [Reference Cisinski and DégliseCD15, Lemma 3.15]. It is quite common for cohomology theories in algebraic geometry to have some kind of trace or transfer morphisms, see Example 14 for a list of examples. Many cohomology theories in algebraic geometry satisfy (G1), see also Gersten’s Conjecture for algebraic
$\mathbb{Z}[\frac{1}{p}]$
-coefficients), [Reference Elmanto and KhanEK18], [Reference Cisinski and DégliseCD15, Lemma 3.15]. It is quite common for cohomology theories in algebraic geometry to have some kind of trace or transfer morphisms, see Example 14 for a list of examples. Many cohomology theories in algebraic geometry satisfy (G1), see also Gersten’s Conjecture for algebraic
![]() $K$
-theory [Reference QuillenQui73, Theorem 7.5.11], or Cousin complexes in the Bloch–Ogus–Gabber theorem [Reference Colliot-Thélene, Hoobler and KahnCTHK]. In particular, the cohomology theories representable in the motivic stable homotopy category that we are interested in satisfy (G1), [Reference Kelly and MorrowKM18, Remark 3.2], [Reference KellyKel17, Theorem 3.3.1].
$K$
-theory [Reference QuillenQui73, Theorem 7.5.11], or Cousin complexes in the Bloch–Ogus–Gabber theorem [Reference Colliot-Thélene, Hoobler and KahnCTHK]. In particular, the cohomology theories representable in the motivic stable homotopy category that we are interested in satisfy (G1), [Reference Kelly and MorrowKM18, Remark 3.2], [Reference KellyKel17, Theorem 3.3.1].
Condition (G2) seems newer. It is true for algebraic
![]() $K$
-theory, or more generally, for nilpotent invariant theories commuting with filtered colimits which satisfy “Milnor” excision, [Reference Kelly and MorrowKM18, Lemma 3.5]. The author is currently working with Elmanto, Hoyois, and Iwasa to prove “Milnor” excision for
$K$
-theory, or more generally, for nilpotent invariant theories commuting with filtered colimits which satisfy “Milnor” excision, [Reference Kelly and MorrowKM18, Lemma 3.5]. The author is currently working with Elmanto, Hoyois, and Iwasa to prove “Milnor” excision for
![]() $SH$
with
$SH$
with
![]() $\mathbb{Z}[\frac{1}{p}]$
-coefficients. See also Bhatt and Mathew’s newly minted arc-topology [Reference Bhatt and MathewBM18, Theorem 1.6].
$\mathbb{Z}[\frac{1}{p}]$
-coefficients. See also Bhatt and Mathew’s newly minted arc-topology [Reference Bhatt and MathewBM18, Theorem 1.6].
The problem—non-Nagataness. One of the first things one might try when comparing the cohomology of a finer topology
![]() $\unicode[STIX]{x1D706}$
with a coarser one
$\unicode[STIX]{x1D706}$
with a coarser one
![]() $\unicode[STIX]{x1D70E}$
is the change of topology spectral sequence
$\unicode[STIX]{x1D70E}$
is the change of topology spectral sequence
If one can show that
![]() $H_{\unicode[STIX]{x1D706}}^{p}(P,F_{\unicode[STIX]{x1D706}})=0$
(for
$H_{\unicode[STIX]{x1D706}}^{p}(P,F_{\unicode[STIX]{x1D706}})=0$
(for
![]() $p>0$
and
$p>0$
and
![]() $F_{\unicode[STIX]{x1D706}}(P)=F(P)$
) for schemes
$F_{\unicode[STIX]{x1D706}}(P)=F(P)$
) for schemes
![]() $P$
in a family inducing a conservative family of fiber functors of the
$P$
in a family inducing a conservative family of fiber functors of the
![]() $\unicode[STIX]{x1D70E}$
-topos, it follows that
$\unicode[STIX]{x1D70E}$
-topos, it follows that
![]() $(\text{}\underline{H}_{\unicode[STIX]{x1D706}}^{q}F)_{\unicode[STIX]{x1D70E}}=0$
(for
$(\text{}\underline{H}_{\unicode[STIX]{x1D706}}^{q}F)_{\unicode[STIX]{x1D70E}}=0$
(for
![]() $p>0$
and
$p>0$
and
![]() $F_{\unicode[STIX]{x1D70E}}=F_{\unicode[STIX]{x1D706}}$
), the spectral sequence collapses, and one is done. If
$F_{\unicode[STIX]{x1D70E}}=F_{\unicode[STIX]{x1D706}}$
), the spectral sequence collapses, and one is done. If
![]() $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706})=(\text{Zariski},\acute{\text{e}}\text{tale})$
then this would be to show that
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706})=(\text{Zariski},\acute{\text{e}}\text{tale})$
then this would be to show that
![]() $H_{\operatorname{et}}^{p}(-,F_{\operatorname{et}})$
vanishes on all local rings. In our setting where
$H_{\operatorname{et}}^{p}(-,F_{\operatorname{et}})$
vanishes on all local rings. In our setting where
![]() $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706})=(\operatorname{cdh},l\operatorname{dh})$
it amounts to showing that
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706})=(\operatorname{cdh},l\operatorname{dh})$
it amounts to showing that
![]() $H_{l\operatorname{dh}}^{p}(-,F_{l\operatorname{dh}})$
vanishes on finite rank Hensel valuation rings, (Appendix B).
$H_{l\operatorname{dh}}^{p}(-,F_{l\operatorname{dh}})$
vanishes on finite rank Hensel valuation rings, (Appendix B).
To prove this vanishing, one would like to use a structure of trace morphisms on
![]() $F$
(as formalized in Definition 13) and the well-known fact that every
$F$
(as formalized in Definition 13) and the well-known fact that every
![]() $l\operatorname{dh}$
-covering of (the spectrum of) a Hensel valuation ring is refinable by a finite flat surjective morphism of degree prime to
$l\operatorname{dh}$
-covering of (the spectrum of) a Hensel valuation ring is refinable by a finite flat surjective morphism of degree prime to
![]() $l$
, via something like the following well-known lemma:
$l$
, via something like the following well-known lemma:
Lemma 2. (Lemma 15, [Reference KellyKel17, Lemma 2.1.8])
Suppose that
![]() $F$
is a
$F$
is a
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces in the sense of Definition 13, and
$\mathbb{Z}_{(l)}$
-linear presheaf with traces in the sense of Definition 13, and
![]() $f:Y\rightarrow X$
a finite flat surjective morphism of degree prime to
$f:Y\rightarrow X$
a finite flat surjective morphism of degree prime to
![]() $l$
. Then the complex
$l$
. Then the complex
is exact.
The problem is that finite flat algebras over Hensel valuation rings are not necessarily products of Hensel valuation rings. We can try to return to Hensel valuation rings by normalizing (cf. Lemma 16), but then this takes us out of the category of finite algebras. To summarize:
Problem. Given a Hensel valuation ring
![]() $R$
and a finite faithfully flat
$R$
and a finite faithfully flat
![]() $R$
-algebra
$R$
-algebra
![]() $R\rightarrow A$
, in general, there is no
$R\rightarrow A$
, in general, there is no
![]() $A$
-algebra
$A$
-algebra
![]() $A^{\prime }$
such that
$A^{\prime }$
such that
![]() $R\rightarrow A^{\prime }$
is finite faithfully flat and
$R\rightarrow A^{\prime }$
is finite faithfully flat and
![]() $A^{\prime }$
is a product of Hensel valuation rings.
$A^{\prime }$
is a product of Hensel valuation rings.
The normalization
![]() $R\rightarrow \widetilde{A}$
is a product of Hensel valuation rings, and faithfully flat, but unless
$R\rightarrow \widetilde{A}$
is a product of Hensel valuation rings, and faithfully flat, but unless
![]() $\operatorname{Frac}(\widetilde{A})/\operatorname{Frac}(R)$
is finite separable and
$\operatorname{Frac}(\widetilde{A})/\operatorname{Frac}(R)$
is finite separable and
![]() $R$
is discrete [Reference BourbakiBou64, Chapter 6, Section 8, No. 5, Theorem 2, Corollary 1], the morphism
$R$
is discrete [Reference BourbakiBou64, Chapter 6, Section 8, No. 5, Theorem 2, Corollary 1], the morphism
![]() $R\rightarrow \widetilde{A}$
is in general no longer finite, not even for a general discrete valuation ring
$R\rightarrow \widetilde{A}$
is in general no longer finite, not even for a general discrete valuation ring
![]() $R$
(cf. Example 18).
$R$
(cf. Example 18).
The solution—pseudo-normalizations. The observation which rescues us is that
![]() $\mathbb{Z}[\frac{1}{p}]$
-motivic cohomology, and more generally the sheaves we are interested in, are invariant under universal homeomorphism. Since we can restrict our attention to finite rank Hensel valuation rings (cf. Corollary A.3), and all residue field extensions of a finite extension of valuation rings are finite, we do not have to normalize to catch all the information in the normalization that we need.
$\mathbb{Z}[\frac{1}{p}]$
-motivic cohomology, and more generally the sheaves we are interested in, are invariant under universal homeomorphism. Since we can restrict our attention to finite rank Hensel valuation rings (cf. Corollary A.3), and all residue field extensions of a finite extension of valuation rings are finite, we do not have to normalize to catch all the information in the normalization that we need.
Lemma 3. (See Lemma 20)
Suppose
![]() $R$
is a finite rank Hensel valuation ring and
$R$
is a finite rank Hensel valuation ring and
![]() $R\rightarrow A$
a finite faithfully flat algebra. Then there exists an
$R\rightarrow A$
a finite faithfully flat algebra. Then there exists an
![]() $A$
-algebra
$A$
-algebra
![]() $A^{\prime }$
such that
$A^{\prime }$
such that
![]() $R\rightarrow A^{\prime }$
is finite faithfully flat and
$R\rightarrow A^{\prime }$
is finite faithfully flat and
![]() $\operatorname{Spec}(\widetilde{A^{\prime }})\rightarrow \operatorname{Spec}(A^{\prime })$
induces an isomorphism on underlying topological spaces and all residue fields.
$\operatorname{Spec}(\widetilde{A^{\prime }})\rightarrow \operatorname{Spec}(A^{\prime })$
induces an isomorphism on underlying topological spaces and all residue fields.
Since our sheaves do not distinguish between
![]() $A^{\prime }$
and the (product of) valuation ring(s)
$A^{\prime }$
and the (product of) valuation ring(s)
![]() $\widetilde{A^{\prime }}$
, we can use
$\widetilde{A^{\prime }}$
, we can use
![]() $A^{\prime }$
as though it were a valuation ring. To work with this lemma we introduce the notion of pseudo-normalization.
$A^{\prime }$
as though it were a valuation ring. To work with this lemma we introduce the notion of pseudo-normalization.
Definition 4. (See Definition 19)
Let
![]() $A$
be a ring and
$A$
be a ring and
![]() $A\rightarrow B$
an
$A\rightarrow B$
an
![]() $A$
-algebra. Define a pseudo-integral closure
Footnote
3
of
$A$
-algebra. Define a pseudo-integral closure
Footnote
3
of
![]() $A$
in
$A$
in
![]() $B$
to be a finite sub-
$B$
to be a finite sub-
![]() $A$
-algebra
$A$
-algebra
of the integral closure
![]() $B^{\operatorname{ic}}$
of
$B^{\operatorname{ic}}$
of
![]() $A$
in
$A$
in
![]() $B$
such that
$B$
such that
![]() $\operatorname{Spec}(B^{\operatorname{pic}})\rightarrow \operatorname{Spec}(B^{\operatorname{ic}})$
induces an isomorphism on topological spaces and residue fields. A pseudo-normalization of
$\operatorname{Spec}(B^{\operatorname{pic}})\rightarrow \operatorname{Spec}(B^{\operatorname{ic}})$
induces an isomorphism on topological spaces and residue fields. A pseudo-normalization of
![]() $A$
is a pseudo-integral closure of
$A$
is a pseudo-integral closure of
![]() $A$
in its normalization
$A$
in its normalization
So the lemma above now becomes:
Lemma 5. (See Lemma 20)
Every finite faithfully flat algebra
![]() $A$
over a finite rank Hensel valuation ring admits a pseudo-normalization
$A$
over a finite rank Hensel valuation ring admits a pseudo-normalization
![]() $A\rightarrow \breve{A}$
.
$A\rightarrow \breve{A}$
.
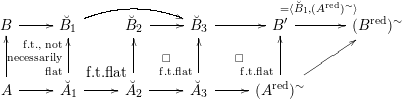
Outline. In Section 2 (resp. 3, resp. 4), we recall some well-known material on universal homeomorphisms (resp. presheaves with traces, resp. Hensel valuation rings). An interesting observation is that a morphism of schemes becomes an isomorphism of
![]() $l\operatorname{dh}$
-sheaves under Yoneda if and only if it is a universal homeomorphism, Corollary 9, Remark 10, (valid for any
$l\operatorname{dh}$
-sheaves under Yoneda if and only if it is a universal homeomorphism, Corollary 9, Remark 10, (valid for any
![]() $l\neq p$
). The
$l\neq p$
). The
![]() $h$
-version of this statement is well-known and due to Voevodsky [Reference VoevodskyVoe96] for excellent Noetherian schemes and Rydh [Reference RydhRyd10] in general.
$h$
-version of this statement is well-known and due to Voevodsky [Reference VoevodskyVoe96] for excellent Noetherian schemes and Rydh [Reference RydhRyd10] in general.
In Section 5, we introduce the notion of pseudo-integral closure and pseudo-normalization, and develop some basic properties.
Sections 6–8 (pages 199–205) contain our proof.
In Section 6, the condition (G1) appears, and we use it to show that for Hensel valuation rings
![]() $R$
we have
$R$
we have
![]() $F(R)\cong F_{l\operatorname{dh}}(R)$
, Proposition 24.
$F(R)\cong F_{l\operatorname{dh}}(R)$
, Proposition 24.
In Section 7, we continue using (G1) to show that traces on
![]() $F$
induce traces on
$F$
induce traces on
![]() $F_{l\operatorname{dh}}$
, Proposition 29.
$F_{l\operatorname{dh}}$
, Proposition 29.
Section 8 (pages 203–205) contains our main theorem (Theorem 30) and the rest of its proof.
In Appendix A, we recall the definitions of the
![]() $\operatorname{cdh}$
- and
$\operatorname{cdh}$
- and
![]() $l\operatorname{dh}$
-topologies, and observe that for finite dimensional Noetherian schemes, the class of finite dimensional Hensel valuation rings induces a conservative family of fiber functors.
$l\operatorname{dh}$
-topologies, and observe that for finite dimensional Noetherian schemes, the class of finite dimensional Hensel valuation rings induces a conservative family of fiber functors.
In Appendix B, we confirm that everything we need passes from finite type separated
![]() $S$
-schemes to all quasi-compact separated
$S$
-schemes to all quasi-compact separated
![]() $S$
-schemes just as one would expect.
$S$
-schemes just as one would expect.
Convention. We work with a base scheme
![]() $S$
which will almost always be separated and Noetherian, and often of finite dimension. We write:
$S$
which will almost always be separated and Noetherian, and often of finite dimension. We write:
 $\mathsf{Sch}_{S}$
for the category of separated finite type
$\mathsf{Sch}_{S}$
for the category of separated finite type
 $S$
-schemes. Unless otherwise indicated, presheaf means a presheaf on
$S$
-schemes. Unless otherwise indicated, presheaf means a presheaf on
 $\mathsf{Sch}_{S}$
which is extended to the category
$\mathsf{Sch}_{S}$
which is extended to the category $\mathsf{SCH}_{S}$
of all quasi-compact separated
$\mathsf{SCH}_{S}$
of all quasi-compact separated
 $S$
-schemes by left Kan extension. That is
$S$
-schemes by left Kan extension. That is
 $F(T)=\mathop{\varinjlim }\nolimits_{T\rightarrow X\rightarrow S}F(X)$
where the colimit is over factorizations through
$F(T)=\mathop{\varinjlim }\nolimits_{T\rightarrow X\rightarrow S}F(X)$
where the colimit is over factorizations through
 $X\in \mathsf{Sch}_{S}$
. Another way of saying this, (when
$X\in \mathsf{Sch}_{S}$
. Another way of saying this, (when
 $S$
is quasi-compact and quasi-separated), is that
$S$
is quasi-compact and quasi-separated), is thatpresheaf means an additive functor
 $F:\mathsf{SCH}_{S}^{\operatorname{op}}\rightarrow \operatorname{Ab}$
that commutes with filtered colimits. For more on this see Appendix B.
$F:\mathsf{SCH}_{S}^{\operatorname{op}}\rightarrow \operatorname{Ab}$
that commutes with filtered colimits. For more on this see Appendix B.We use
 $h_{-}:C\rightarrow \mathsf{PreShv}(C);X\mapsto h_{X}$
for the Yoneda functor, and
$h_{-}:C\rightarrow \mathsf{PreShv}(C);X\mapsto h_{X}$
for the Yoneda functor, and $(-)_{\unicode[STIX]{x1D70F}}:\mathsf{PreShv}(C)\rightarrow \mathsf{Shv}_{\unicode[STIX]{x1D70F}}(C);F\mapsto F_{\unicode[STIX]{x1D70F}}$
for the sheafification functor. We write
$(-)_{\unicode[STIX]{x1D70F}}:\mathsf{PreShv}(C)\rightarrow \mathsf{Shv}_{\unicode[STIX]{x1D70F}}(C);F\mapsto F_{\unicode[STIX]{x1D70F}}$
for the sheafification functor. We write $\text{}\underline{H}_{\unicode[STIX]{x1D70F}}^{n}F$
for the presheaf
$\text{}\underline{H}_{\unicode[STIX]{x1D70F}}^{n}F$
for the presheaf
 $H_{\unicode[STIX]{x1D70F}}^{n}(-,F_{\unicode[STIX]{x1D70F}})$
associated to a presheaf
$H_{\unicode[STIX]{x1D70F}}^{n}(-,F_{\unicode[STIX]{x1D70F}})$
associated to a presheaf
 $F$
. This paper’s topologies (principally
$F$
. This paper’s topologies (principally
 $\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
) are classically defined on
$\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
) are classically defined on
 $\mathsf{Sch}_{S}$
for
$\mathsf{Sch}_{S}$
for
 $S$
Noetherian. We extend them to
$S$
Noetherian. We extend them to
 $\mathsf{SCH}_{S}$
in the canonical way (cf. Appendix B).
$\mathsf{SCH}_{S}$
in the canonical way (cf. Appendix B). $Q(A)$
is the total ring of fractions of a ring
$Q(A)$
is the total ring of fractions of a ring
 $A$
. We will only ever apply this to reduced rings.
$A$
. We will only ever apply this to reduced rings. $l$
and
$l$
and
 $p$
are always distinct primes.
$p$
are always distinct primes.
2 Universal homeomorphisms
In this section, we recall some basic material on universal homeomorphisms (
![]() $\operatorname{uh}$
), and show that
$\operatorname{uh}$
), and show that
![]() $l\operatorname{dh}$
-sheafification preserves
$l\operatorname{dh}$
-sheafification preserves
![]() $\operatorname{uh}$
-invariances. For some background on the
$\operatorname{uh}$
-invariances. For some background on the
![]() $l\operatorname{dh}$
-topology for Noetherian, and non-Noetherian schemes, we direct the reader to appendices A and B, respectively.
$l\operatorname{dh}$
-topology for Noetherian, and non-Noetherian schemes, we direct the reader to appendices A and B, respectively.
Definition 6. A morphism of schemes
![]() $f:Y\rightarrow X$
is a universal homeomorphism or
$f:Y\rightarrow X$
is a universal homeomorphism or
![]() $\operatorname{uh}$
if it satisfies the following equivalent conditions.
$\operatorname{uh}$
if it satisfies the following equivalent conditions.
(1) For every
 $X$
-scheme
$X$
-scheme
 $T\rightarrow X$
, the morphism
$T\rightarrow X$
, the morphism
 $T\times _{X}Y\rightarrow T$
induces a homeomorphism on the underlying topological spaces.
$T\times _{X}Y\rightarrow T$
induces a homeomorphism on the underlying topological spaces.(2) [Stacks, Tag 01S4, Tag 01S3]
 $f$
is a homeomorphism, and for every
$f$
is a homeomorphism, and for every
 $y\in Y$
, the field extension
$y\in Y$
, the field extension
 $k(y)/k(f(y))$
is purely inseparable.
$k(y)/k(f(y))$
is purely inseparable.(3) [Reference GrothendieckEGAIV4, Corollary 18.12.11]
 $f$
is integral, surjective and universally injective.
$f$
is integral, surjective and universally injective.(4) [Stacks, Tag 01WM]
 $f$
is affine, surjective, and universally injective.
$f$
is affine, surjective, and universally injective.
Note there are no finiteness conditions. There are universal homeomorphisms that are not of finite type, pertinently Example 18, and finite universal homeomorphisms that are not finitely presented. For example,
![]() $A=\mathop{\varinjlim }\nolimits_{n\rightarrow \infty }\mathbb{F}_{p}[x_{1},\ldots ,x_{n}]/\langle x_{i}x_{j}:i\neq j\rangle$
and the map
$A=\mathop{\varinjlim }\nolimits_{n\rightarrow \infty }\mathbb{F}_{p}[x_{1},\ldots ,x_{n}]/\langle x_{i}x_{j}:i\neq j\rangle$
and the map
![]() $\unicode[STIX]{x1D719}:A\rightarrow A;x_{1}\mapsto x_{1}^{p}$
. To generate the kernel of
$\unicode[STIX]{x1D719}:A\rightarrow A;x_{1}\mapsto x_{1}^{p}$
. To generate the kernel of
![]() $A[y]\rightarrow A;\sum a_{m}y^{m}\mapsto \sum \unicode[STIX]{x1D719}(a_{m})x_{1}^{m}$
, in addition to
$A[y]\rightarrow A;\sum a_{m}y^{m}\mapsto \sum \unicode[STIX]{x1D719}(a_{m})x_{1}^{m}$
, in addition to
![]() $y^{p}-x_{1}$
one needs all the
$y^{p}-x_{1}$
one needs all the
![]() $yx_{n}$
for
$yx_{n}$
for
![]() $n>1$
.
$n>1$
.
Lemma 7. Suppose that
![]() $Y\rightarrow X$
is a universal homeomorphism, and
$Y\rightarrow X$
is a universal homeomorphism, and
![]() ${\mathcal{A}}\subseteq {\mathcal{O}}_{Y}$
is a sub-
${\mathcal{A}}\subseteq {\mathcal{O}}_{Y}$
is a sub-
![]() ${\mathcal{O}}_{X}$
-algebra. Then both of
${\mathcal{O}}_{X}$
-algebra. Then both of
![]() $Y\rightarrow \text{}\underline{\operatorname{Spec}}({\mathcal{A}})\rightarrow X$
are universal homeomorphisms.
$Y\rightarrow \text{}\underline{\operatorname{Spec}}({\mathcal{A}})\rightarrow X$
are universal homeomorphisms.
Proof. By Definition 6(3) it suffices to prove that
![]() $Y\rightarrow \text{}\underline{\operatorname{Spec}}({\mathcal{A}})$
is surjective. But this follows from integrality and injectivity of
$Y\rightarrow \text{}\underline{\operatorname{Spec}}({\mathcal{A}})$
is surjective. But this follows from integrality and injectivity of
![]() ${\mathcal{A}}\subseteq {\mathcal{O}}_{Y}$
, [Stacks, Tag 00GQ].◻
${\mathcal{A}}\subseteq {\mathcal{O}}_{Y}$
, [Stacks, Tag 00GQ].◻
Recall that a morphism of schemes
![]() $Y\rightarrow X$
is completely decomposed if it induces a surjection
$Y\rightarrow X$
is completely decomposed if it induces a surjection
![]() $Y(K)\rightarrow X(K)$
of
$Y(K)\rightarrow X(K)$
of
![]() $K$
-points for every field
$K$
-points for every field
![]() $K$
.
$K$
.
Lemma 8. Let
![]() $S$
be a Noetherian separated scheme of positive characteristic
$S$
be a Noetherian separated scheme of positive characteristic
![]() $p$
. Every universal homeomorphism
$p$
. Every universal homeomorphism
![]() $Y\rightarrow X$
in
$Y\rightarrow X$
in
![]() $\mathsf{Sch}_{S}$
is refinable by a composition
$\mathsf{Sch}_{S}$
is refinable by a composition
![]() $Y_{1}\rightarrow Y_{0}\rightarrow X$
such that
$Y_{1}\rightarrow Y_{0}\rightarrow X$
such that
![]() $Y_{0}\rightarrow X$
is proper and completely decomposed, and
$Y_{0}\rightarrow X$
is proper and completely decomposed, and
![]() $Y_{1}\rightarrow Y_{0}$
is finite flat surjective and locally of degree a power of
$Y_{1}\rightarrow Y_{0}$
is finite flat surjective and locally of degree a power of
![]() $p$
.
$p$
.
Proof. We reproduce the standard proof using Raynaud–Gruson flatification and induction on the dimension. The initial case is dimension
![]() $-1$
, that is, the empty scheme. Suppose that
$-1$
, that is, the empty scheme. Suppose that
![]() $Y\rightarrow X$
is a universal homeomorphism with
$Y\rightarrow X$
is a universal homeomorphism with
![]() $\dim X=n\geqslant 0$
, and suppose that the statement is true for a target scheme of dimension
$\dim X=n\geqslant 0$
, and suppose that the statement is true for a target scheme of dimension
![]() ${<}n$
. Replacing
${<}n$
. Replacing
![]() $X$
and
$X$
and
![]() $Y$
with their reductions, we can assume that
$Y$
with their reductions, we can assume that
![]() $Y\rightarrow X$
is generically flat. In this case, by Raynaud–Gruson flatification [Reference Raynaud and GrusonRG71, Theorem 5.2.2], there exists a nowhere dense closed subscheme
$Y\rightarrow X$
is generically flat. In this case, by Raynaud–Gruson flatification [Reference Raynaud and GrusonRG71, Theorem 5.2.2], there exists a nowhere dense closed subscheme
![]() $Z\subset X$
such that the strict transform
$Z\subset X$
such that the strict transform
![]() $Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is globally flat. On the other hand, as
$Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is globally flat. On the other hand, as
![]() $Y\rightarrow X$
is an integral morphism of finite type, it is finite. Therefore,
$Y\rightarrow X$
is an integral morphism of finite type, it is finite. Therefore,
![]() $Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is flat and finite. Moreover, as
$Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is flat and finite. Moreover, as
![]() $Y\rightarrow X$
is a universal homeomorphism, for each generic point
$Y\rightarrow X$
is a universal homeomorphism, for each generic point
![]() $\unicode[STIX]{x1D709}\in X$
with corresponding point
$\unicode[STIX]{x1D709}\in X$
with corresponding point
![]() $\unicode[STIX]{x1D702}\in Y$
, the finite field extension
$\unicode[STIX]{x1D702}\in Y$
, the finite field extension
![]() $k(\unicode[STIX]{x1D702})/k(\unicode[STIX]{x1D709})$
is purely inseparable. In particular, as
$k(\unicode[STIX]{x1D702})/k(\unicode[STIX]{x1D709})$
is purely inseparable. In particular, as
![]() $Y^{\prime }$
and
$Y^{\prime }$
and
![]() $\operatorname{Bl}_{Z}X$
are reduced,
$\operatorname{Bl}_{Z}X$
are reduced,
![]() $Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is locally of degree a power of
$Y^{\prime }\rightarrow \operatorname{Bl}_{Z}X$
is locally of degree a power of
![]() $p$
. Using the Noetherian inductive hypothesis to choose a refinement
$p$
. Using the Noetherian inductive hypothesis to choose a refinement
![]() $W_{1}\rightarrow W_{0}\rightarrow Z$
of the universal homeomorphism
$W_{1}\rightarrow W_{0}\rightarrow Z$
of the universal homeomorphism
![]() $Y\times _{X}Z\rightarrow Z$
, we have produced the desired refinement
$Y\times _{X}Z\rightarrow Z$
, we have produced the desired refinement
![]() $W_{1}\sqcup Y^{\prime }\rightarrow W_{0}\sqcup \operatorname{Bl}_{Z}X\rightarrow X$
of
$W_{1}\sqcup Y^{\prime }\rightarrow W_{0}\sqcup \operatorname{Bl}_{Z}X\rightarrow X$
of
![]() $Y\rightarrow X$
.◻
$Y\rightarrow X$
.◻
Corollary 9. Let
![]() $S$
be a Noetherian scheme of positive characteristic
$S$
be a Noetherian scheme of positive characteristic
![]() $p\neq l$
and
$p\neq l$
and
![]() $f:Y\rightarrow X$
a universal homeomorphism in
$f:Y\rightarrow X$
a universal homeomorphism in
![]() $\mathsf{Sch}_{S}$
. Then the image
$\mathsf{Sch}_{S}$
. Then the image
![]() $(h_{f})_{l\operatorname{dh}}\in \mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
of
$(h_{f})_{l\operatorname{dh}}\in \mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
of
![]() $f$
is an isomorphism.
$f$
is an isomorphism.
Remark 10. In fact, the converse is also true: [Reference VoevodskyVoe96, Theorem 3.2.9] and [Reference RydhRyd10, Theorem 8.16] say that the image of
![]() $(h)_{\operatorname{h}}:\mathsf{Sch}_{S}\rightarrow \mathsf{Shv}_{\operatorname{h}}(\mathsf{Sch}_{S})$
is equivalent to the localization of
$(h)_{\operatorname{h}}:\mathsf{Sch}_{S}\rightarrow \mathsf{Shv}_{\operatorname{h}}(\mathsf{Sch}_{S})$
is equivalent to the localization of
![]() $\mathsf{Sch}_{S}$
at the class
$\mathsf{Sch}_{S}$
at the class
![]() $\operatorname{uh}$
. As
$\operatorname{uh}$
. As
![]() $\operatorname{uh}$
is a right multiplicative system and satisfies the 2-out-of-6 property, it follows that a morphism in
$\operatorname{uh}$
is a right multiplicative system and satisfies the 2-out-of-6 property, it follows that a morphism in
![]() $\mathsf{Sch}_{S}$
is in
$\mathsf{Sch}_{S}$
is in
![]() $\operatorname{uh}$
if and only if it becomes an isomorphism in
$\operatorname{uh}$
if and only if it becomes an isomorphism in
![]() $\mathsf{Sch}_{\operatorname{h}}(\mathsf{Sch}_{S})$
, [Reference Kashiwara and SchapiraKS06, 7.1.20]. Since
$\mathsf{Sch}_{\operatorname{h}}(\mathsf{Sch}_{S})$
, [Reference Kashiwara and SchapiraKS06, 7.1.20]. Since
![]() $\mathsf{Sch}_{S}\rightarrow \mathsf{Shv}_{\operatorname{h}}(\mathsf{Sch}_{S})$
factors through
$\mathsf{Sch}_{S}\rightarrow \mathsf{Shv}_{\operatorname{h}}(\mathsf{Sch}_{S})$
factors through
![]() $\mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
, the converse of Corollary 9 follows.
$\mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
, the converse of Corollary 9 follows.
Proof. Surjectivity is a result of
![]() $f$
being (refinable by) an
$f$
being (refinable by) an
![]() $l\operatorname{dh}$
-cover, Lemma 8. For injectivity, consider some
$l\operatorname{dh}$
-cover, Lemma 8. For injectivity, consider some
![]() $s,s^{\prime }\in (h_{Y})_{l\operatorname{dh}}(T)$
sent to the same element of
$s,s^{\prime }\in (h_{Y})_{l\operatorname{dh}}(T)$
sent to the same element of
![]() $(h_{X})_{l\operatorname{dh}}(T)$
. Let
$(h_{X})_{l\operatorname{dh}}(T)$
. Let
![]() $T^{\prime }\rightarrow T$
be an
$T^{\prime }\rightarrow T$
be an
![]() $l\operatorname{dh}$
-cover such that
$l\operatorname{dh}$
-cover such that
![]() $s,s^{\prime }$
can be represented by some morphisms
$s,s^{\prime }$
can be represented by some morphisms
![]() $t,t^{\prime }:T^{\prime }\rightarrow Y$
in
$t,t^{\prime }:T^{\prime }\rightarrow Y$
in
![]() $\mathsf{Sch}_{S}$
with
$\mathsf{Sch}_{S}$
with
![]() $T^{\prime }$
reduced. Possibly refining
$T^{\prime }$
reduced. Possibly refining
![]() $T^{\prime }$
, we can assume that
$T^{\prime }$
, we can assume that
![]() $ft=ft^{\prime }$
. Let
$ft=ft^{\prime }$
. Let
![]() $\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}$
be the generic points of
$\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}$
be the generic points of
![]() $T^{\prime }$
. As
$T^{\prime }$
. As
![]() $f:Y\rightarrow X$
is a universal homeomorphism, it is injective on the underlying topological space, and all residue field extensions are purely inseparable. Consequently,
$f:Y\rightarrow X$
is a universal homeomorphism, it is injective on the underlying topological space, and all residue field extensions are purely inseparable. Consequently,
![]() $\hom (\amalg \unicode[STIX]{x1D702}_{i},Y)\rightarrow \hom (\amalg \unicode[STIX]{x1D702}_{i},X)$
is injective, so
$\hom (\amalg \unicode[STIX]{x1D702}_{i},Y)\rightarrow \hom (\amalg \unicode[STIX]{x1D702}_{i},X)$
is injective, so
![]() $t|_{\amalg \unicode[STIX]{x1D702}_{i}}=t^{\prime }|_{\amalg \unicode[STIX]{x1D702}_{i}}$
. But
$t|_{\amalg \unicode[STIX]{x1D702}_{i}}=t^{\prime }|_{\amalg \unicode[STIX]{x1D702}_{i}}$
. But
![]() $Y\rightarrow X$
is separated, and
$Y\rightarrow X$
is separated, and
![]() $T^{\prime }$
reduced, so
$T^{\prime }$
reduced, so
![]() $t=t^{\prime }$
.◻
$t=t^{\prime }$
.◻
Corollary 11. Let
![]() $S$
be a Noetherian scheme of positive characteristic
$S$
be a Noetherian scheme of positive characteristic
![]() $p\neq l$
. For any presheaf
$p\neq l$
. For any presheaf
![]() $F$
and
$F$
and
![]() $n\geqslant 0$
, the associated presheaf
$n\geqslant 0$
, the associated presheaf
![]() $(\text{}\underline{H}_{l\operatorname{dh}}^{n}F)(-)=H_{l\operatorname{dh}}^{n}(-,F_{l\operatorname{dh}})$
is
$(\text{}\underline{H}_{l\operatorname{dh}}^{n}F)(-)=H_{l\operatorname{dh}}^{n}(-,F_{l\operatorname{dh}})$
is
![]() $\operatorname{uh}$
-invariant.
$\operatorname{uh}$
-invariant.
Proof. Let
![]() $F_{l\operatorname{dh}}\rightarrow I^{\bullet }$
be an injective resolution in
$F_{l\operatorname{dh}}\rightarrow I^{\bullet }$
be an injective resolution in
![]() $\mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
. Then we have
$\mathsf{Shv}_{l\operatorname{dh}}(\mathsf{Sch}_{S})$
. Then we have
![]() $(\text{}\underline{H}_{l\operatorname{dh}}^{n}F)(-)=H^{n}(\hom _{\mathsf{Shv}_{l\operatorname{dh}}}((h_{-})_{l\operatorname{dh}},I^{\bullet }))$
. But Corollary 9 says that
$(\text{}\underline{H}_{l\operatorname{dh}}^{n}F)(-)=H^{n}(\hom _{\mathsf{Shv}_{l\operatorname{dh}}}((h_{-})_{l\operatorname{dh}},I^{\bullet }))$
. But Corollary 9 says that
![]() $(h_{-})_{l\operatorname{dh}}$
sends universal homeomorphisms to isomorphisms. Hence, the same is true of
$(h_{-})_{l\operatorname{dh}}$
sends universal homeomorphisms to isomorphisms. Hence, the same is true of
![]() $\text{}\underline{H}_{l\operatorname{dh}}^{n}F$
.◻
$\text{}\underline{H}_{l\operatorname{dh}}^{n}F$
.◻
3 Traces and
 $\operatorname{fps}l^{\prime }$
-descent
$\operatorname{fps}l^{\prime }$
-descent
This section contains material on presheaves with traces from [Reference KellyKel17] included for the convenience of the reader.
Definition 12. We abbreviate finite flat surjective to
![]() $\operatorname{fps}$
, and finite flat surjective of degree prime to
$\operatorname{fps}$
, and finite flat surjective of degree prime to
![]() $l$
to
$l$
to
![]() $\operatorname{fps}l^{\prime }$
.
$\operatorname{fps}l^{\prime }$
.
Definition 13. [Reference KellyKel17, Definition 2.1.3]
Let
![]() ${\mathcal{S}}$
be a category of schemes admitting fiber products. A structure of traces on a presheaf
${\mathcal{S}}$
be a category of schemes admitting fiber products. A structure of traces on a presheaf
![]() $F:{\mathcal{S}}^{op}\rightarrow Ab$
is a morphism
$F:{\mathcal{S}}^{op}\rightarrow Ab$
is a morphism
![]() $\operatorname{Tr}_{f}:F(Y)\rightarrow F(X)$
for every
$\operatorname{Tr}_{f}:F(Y)\rightarrow F(X)$
for every
![]() $\operatorname{fps}$
morphism
$\operatorname{fps}$
morphism
![]() $f:Y\rightarrow X$
, satisfying the following axioms.
$f:Y\rightarrow X$
, satisfying the following axioms.
(1) (Add) We have
 $\operatorname{Tr}_{f\amalg f^{\prime }}=\operatorname{Tr}_{f}\oplus \operatorname{Tr}_{f^{\prime }}$
for every pair
$\operatorname{Tr}_{f\amalg f^{\prime }}=\operatorname{Tr}_{f}\oplus \operatorname{Tr}_{f^{\prime }}$
for every pair
 $Y\stackrel{f}{\rightarrow }X$
,
$Y\stackrel{f}{\rightarrow }X$
,
 $Y^{\prime }\stackrel{f^{\prime }}{\rightarrow }X^{\prime }$
of
$Y^{\prime }\stackrel{f^{\prime }}{\rightarrow }X^{\prime }$
of
 $\operatorname{fps}$
morphisms.
$\operatorname{fps}$
morphisms.(2) (Fon) We have
 $\operatorname{Tr}_{f}\circ \operatorname{Tr}_{g}=\operatorname{Tr}_{f\circ g}$
for every composable pair
$\operatorname{Tr}_{f}\circ \operatorname{Tr}_{g}=\operatorname{Tr}_{f\circ g}$
for every composable pair
 $W\stackrel{g}{\rightarrow }Y\stackrel{f}{\rightarrow }X$
of
$W\stackrel{g}{\rightarrow }Y\stackrel{f}{\rightarrow }X$
of
 $\operatorname{fps}$
morphisms.
$\operatorname{fps}$
morphisms.(3) (CdB) We have
 $F(p)\circ \operatorname{Tr}_{f}=\operatorname{Tr}_{g}\circ F(q)$
for every
$F(p)\circ \operatorname{Tr}_{f}=\operatorname{Tr}_{g}\circ F(q)$
for every
 $\operatorname{fps}$
morphism
$\operatorname{fps}$
morphism
 $f:Y\rightarrow X$
and every cartesian square
$f:Y\rightarrow X$
and every cartesian square 
(4) (Deg) We have
 $\operatorname{Tr}_{f}\circ F(f)=d\cdot \operatorname{id}_{F(X)}$
for every
$\operatorname{Tr}_{f}\circ F(f)=d\cdot \operatorname{id}_{F(X)}$
for every
 $\operatorname{fps}$
morphism
$\operatorname{fps}$
morphism
 $f:Y\rightarrow X$
of constant degree
$f:Y\rightarrow X$
of constant degree
 $d$
.
$d$
.
A presheaf equipped with a structure of traces is called a presheaf with traces. A presheaf with traces taking values in the category of
![]() $R$
-modules for some ring
$R$
-modules for some ring
![]() $R$
, is called a presheaf of
$R$
, is called a presheaf of
![]() $R$
-modules with traces or an
$R$
-modules with traces or an
![]() $R$
-linear presheaf with traces.
$R$
-linear presheaf with traces.
Example 14. (For these and more examples see [Reference KellyKel17, Example 2.1.4])
(1) Every constant additive presheaf has a unique structure of traces determined by the axioms (Add) and (Deg).
(2) The trace and determinant equip
 $({\mathcal{O}},+)$
and
$({\mathcal{O}},+)$
and
 $({\mathcal{O}}^{\ast },\ast )$
respectively with a structure of traces, [Reference KellyKel17, Example 2.1.4(vii)].
$({\mathcal{O}}^{\ast },\ast )$
respectively with a structure of traces, [Reference KellyKel17, Example 2.1.4(vii)].(3) If
 $F$
is a presheaf with traces, then the associated Nisnevich sheaf
$F$
is a presheaf with traces, then the associated Nisnevich sheaf
 $F_{\mathsf{Nis}}$
inherits a unique structure of traces compatible with the canonical morphism
$F_{\mathsf{Nis}}$
inherits a unique structure of traces compatible with the canonical morphism
 $F\rightarrow F_{\mathsf{Nis}}$
, [Reference KellyKel17, Corollary 2.1.13]. This is essentially because a finite algebra over a Hensel local ring is a product of Hensel local rings.
$F\rightarrow F_{\mathsf{Nis}}$
, [Reference KellyKel17, Corollary 2.1.13]. This is essentially because a finite algebra over a Hensel local ring is a product of Hensel local rings.(4) Pushforward of vector bundles would induce a structure of traces on higher
 $K$
-theory
$K$
-theory
 $K_{n}$
and homotopy invariant
$K_{n}$
and homotopy invariant
 $K$
-theory
$K$
-theory
 $KH_{n}$
for every
$KH_{n}$
for every
 $n\in \mathbb{Z}$
, except (Deg) is only satisfied Zariski locally. The Nisnevich sheafifications of these sheaves
$n\in \mathbb{Z}$
, except (Deg) is only satisfied Zariski locally. The Nisnevich sheafifications of these sheaves
 $(K_{n})_{\mathsf{Nis}}$
and
$(K_{n})_{\mathsf{Nis}}$
and
 $(KH_{n})_{\mathsf{Nis}}$
have canonical structures of traces (cf. [Reference KellyKel14, Proof of Lemma 3.1]).
$(KH_{n})_{\mathsf{Nis}}$
have canonical structures of traces (cf. [Reference KellyKel14, Proof of Lemma 3.1]).
Lemma 15. (cf. [Reference KellyKel17, Lemma 2.1.8])
Suppose that
![]() $F$
is a
$F$
is a
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces, and
$\mathbb{Z}_{(l)}$
-linear presheaf with traces, and
![]() $X_{\bullet }\rightarrow X_{-1}$
is a simplicial
$X_{\bullet }\rightarrow X_{-1}$
is a simplicial
![]() $X_{-1}$
-scheme such that each
$X_{-1}$
-scheme such that each
![]() $X_{n+1}\rightarrow (\operatorname{cosk}_{n}X_{\bullet })_{n+1}$
is an
$X_{n+1}\rightarrow (\operatorname{cosk}_{n}X_{\bullet })_{n+1}$
is an
![]() $\operatorname{fps}l^{\prime }$
-morphism of constant degree, for example,
$\operatorname{fps}l^{\prime }$
-morphism of constant degree, for example,
![]() $X_{n-1}=Y^{\times _{X}n}$
for some
$X_{n-1}=Y^{\times _{X}n}$
for some
![]() $\operatorname{fps}l^{\prime }$
-morphism of constant degree
$\operatorname{fps}l^{\prime }$
-morphism of constant degree
![]() $Y\rightarrow X$
. Then the complex
$Y\rightarrow X$
. Then the complex
is exact. Here the morphisms are
![]() $\sum (-1)^{i}d_{i}$
.
$\sum (-1)^{i}d_{i}$
.
Consequently,
![]() $F$
is a
$F$
is a
![]() $\operatorname{fps}l^{\prime }$
-sheaf, and we have both
$\operatorname{fps}l^{\prime }$
-sheaf, and we have both
![]() $\check{H}_{\operatorname{fps}l^{\prime }}^{n}(-,F)=0$
, and
$\check{H}_{\operatorname{fps}l^{\prime }}^{n}(-,F)=0$
, and
![]() $H_{\operatorname{fps}l^{\prime }}^{n}(-,F_{\operatorname{fps}l^{\prime }})=0$
for
$H_{\operatorname{fps}l^{\prime }}^{n}(-,F_{\operatorname{fps}l^{\prime }})=0$
for
![]() $n>0$
.
$n>0$
.
Proof. For each
![]() $0\leqslant i<j\leqslant n$
we have the commutative diagram
$0\leqslant i<j\leqslant n$
we have the commutative diagram

All morphisms are
![]() $\operatorname{fps}l^{\prime }$
-morphisms of constant degree, [Stacks, Tag 01GN ]. Setting,
$\operatorname{fps}l^{\prime }$
-morphisms of constant degree, [Stacks, Tag 01GN ]. Setting,
![]() $D_{m}=\deg (X_{m}\rightarrow X_{-1})/\deg (X_{m-1}\rightarrow X_{-1})=\deg (X_{m}\stackrel{d_{i}}{\rightarrow }X_{m-1})$
, the composition
$D_{m}=\deg (X_{m}\rightarrow X_{-1})/\deg (X_{m-1}\rightarrow X_{-1})=\deg (X_{m}\stackrel{d_{i}}{\rightarrow }X_{m-1})$
, the composition
![]() $ba$
is of degree
$ba$
is of degree
![]() $D_{n+1}/D_{n}$
. Now, it follows from the above diagram, that
$D_{n+1}/D_{n}$
. Now, it follows from the above diagram, that
 $$\begin{eqnarray}\displaystyle \frac{1}{D_{n+1}}Tr_{d_{i}}F(d_{j})\stackrel{(Fon)}{=}\frac{1}{D_{n+1}}Tr_{pr_{1}}Tr_{ba}F(ba)F(pr_{2}) & \stackrel{(\text{Deg})}{=} & \displaystyle \frac{1}{D_{n}}Tr_{pr_{1}}F(pr_{2})\nonumber\\ \displaystyle & \stackrel{(CdB)}{=} & \displaystyle \frac{1}{D_{n}}F(d_{j-1})Tr_{d_{i}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{D_{n+1}}Tr_{d_{i}}F(d_{j})\stackrel{(Fon)}{=}\frac{1}{D_{n+1}}Tr_{pr_{1}}Tr_{ba}F(ba)F(pr_{2}) & \stackrel{(\text{Deg})}{=} & \displaystyle \frac{1}{D_{n}}Tr_{pr_{1}}F(pr_{2})\nonumber\\ \displaystyle & \stackrel{(CdB)}{=} & \displaystyle \frac{1}{D_{n}}F(d_{j-1})Tr_{d_{i}}.\nonumber\end{eqnarray}$$
In particular,
![]() $(1/D_{\bullet })Tr_{d_{0}}$
is a chain homotopy between the zero morphism and the identity morphism of the chain complex in the statement.
$(1/D_{\bullet })Tr_{d_{0}}$
is a chain homotopy between the zero morphism and the identity morphism of the chain complex in the statement.
For the second statement, notice that any
![]() $\operatorname{fps}l^{\prime }$
-morphism is refinable by an
$\operatorname{fps}l^{\prime }$
-morphism is refinable by an
![]() $\operatorname{fps}l^{\prime }$
-morphism of constant degree. Hence, the Čech cohomologies of these two classes of morphisms are the same, and moreover, they generate the same topology. Since the colimit over all hypercovers calculates sheaf cohomology, [SGA42, Theorem 7.4.1(2)], vanishing of sheaf cohomology also follows from exactness of the sequence.◻
$\operatorname{fps}l^{\prime }$
-morphism of constant degree. Hence, the Čech cohomologies of these two classes of morphisms are the same, and moreover, they generate the same topology. Since the colimit over all hypercovers calculates sheaf cohomology, [SGA42, Theorem 7.4.1(2)], vanishing of sheaf cohomology also follows from exactness of the sequence.◻
4 Hensel valuation rings
Recall that an integral domain
![]() $R$
is a valuation ring if for all nonzero
$R$
is a valuation ring if for all nonzero
![]() $a\in \operatorname{Frac}(R)$
, we have
$a\in \operatorname{Frac}(R)$
, we have
![]() $a\in R$
or
$a\in R$
or
![]() $a^{-1}\in R$
. Equivalently, the set of ideals of
$a^{-1}\in R$
. Equivalently, the set of ideals of
![]() $R$
is totally ordered by inclusion, [Reference BourbakiBou64, Chapitre VI, §1.2, Théorème 1].
$R$
is totally ordered by inclusion, [Reference BourbakiBou64, Chapitre VI, §1.2, Théorème 1].
A valuation ring
![]() $R$
is a Hensel valuation ring or hvr if it extends uniquely to every finite field extension, [Reference Engler and PrestelEP05, §4.1]. That is, for every finite field extension
$R$
is a Hensel valuation ring or hvr if it extends uniquely to every finite field extension, [Reference Engler and PrestelEP05, §4.1]. That is, for every finite field extension
![]() $L/\operatorname{Frac}(R)$
, there exists a unique valuation ring
$L/\operatorname{Frac}(R)$
, there exists a unique valuation ring
![]() $R^{\prime }\subseteq L$
such that
$R^{\prime }\subseteq L$
such that
![]() $L=\operatorname{Frac}(R^{\prime })$
and
$L=\operatorname{Frac}(R^{\prime })$
and
![]() $R=L\cap R^{\prime }$
. A valuation ring is a hvr if and only if it satisfies Hensel’s Lemma, [Reference Engler and PrestelEP05, Theorem 4.1.3].
$R=L\cap R^{\prime }$
. A valuation ring is a hvr if and only if it satisfies Hensel’s Lemma, [Reference Engler and PrestelEP05, Theorem 4.1.3].
We will frequently use the following lemma. Recall that
![]() $Q(-)$
denotes the total ring of fractions.
$Q(-)$
denotes the total ring of fractions.
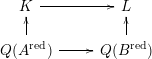
Lemma 16. Let
![]() $R$
be a hvr, let
$R$
be a hvr, let
![]() $R\rightarrow A$
be a finite
$R\rightarrow A$
be a finite
![]() $R$
-algebra, and let
$R$
-algebra, and let
![]() $Q(A^{\operatorname{red}})\rightarrow L$
be a finite morphism with
$Q(A^{\operatorname{red}})\rightarrow L$
be a finite morphism with
![]() $L$
reduced. Then the integral closure
$L$
reduced. Then the integral closure
![]() $A^{\operatorname{ic}}$
of
$A^{\operatorname{ic}}$
of
![]() $A^{\operatorname{red}}$
in
$A^{\operatorname{red}}$
in
![]() $L$
is a product of valuation rings. If
$L$
is a product of valuation rings. If
![]() $A$
and
$A$
and
![]() $L$
are integral domains the induced morphism
$L$
are integral domains the induced morphism
![]() $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)$
is a homeomorphism.
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)$
is a homeomorphism.
Proof. The integral closure
![]() $A^{\operatorname{ic}}$
is the product of the integral closures of the images of
$A^{\operatorname{ic}}$
is the product of the integral closures of the images of
![]() $A^{\operatorname{red}}$
in the residue fields of
$A^{\operatorname{red}}$
in the residue fields of
![]() $L$
, so we can assume
$L$
, so we can assume
![]() $A$
is an integral domain and
$A$
is an integral domain and
![]() $L$
a field. Replacing
$L$
a field. Replacing
![]() $R$
with its imageFootnote
4
in
$R$
with its imageFootnote
4
in
![]() $A$
, we can assume
$A$
, we can assume
![]() $R\rightarrow A$
is injective. Note that since
$R\rightarrow A$
is injective. Note that since
![]() $A$
is finite, the integral closure of
$A$
is finite, the integral closure of
![]() $A$
in
$A$
in
![]() $L$
is equal to the integral closure of
$L$
is equal to the integral closure of
![]() $R$
in
$R$
in
![]() $L$
. Now the first claim follows from the facts that the integral closure of a valuation ring is the intersection of the extensions [Reference Engler and PrestelEP05, Corollary 3.1.4], and since
$L$
. Now the first claim follows from the facts that the integral closure of a valuation ring is the intersection of the extensions [Reference Engler and PrestelEP05, Corollary 3.1.4], and since
![]() $R$
is Henselian, by definition there is a unique extension to
$R$
is Henselian, by definition there is a unique extension to
![]() $L$
. Now,
$L$
. Now,
![]() $R\subseteq A\subseteq A^{\operatorname{ic}}$
are integral extensions of rings so
$R\subseteq A\subseteq A^{\operatorname{ic}}$
are integral extensions of rings so
![]() $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)\rightarrow \operatorname{Spec}(R)$
are surjective [Stacks, Tag 00GQ ]. Since
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)\rightarrow \operatorname{Spec}(R)$
are surjective [Stacks, Tag 00GQ ]. Since
![]() $R\subseteq A\subseteq A^{\operatorname{ic}}$
are integral extensions, the incomparability property implies that
$R\subseteq A\subseteq A^{\operatorname{ic}}$
are integral extensions, the incomparability property implies that
![]() $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)\rightarrow \operatorname{Spec}(R)$
are injective. Finally, since the prime ideals of
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)\rightarrow \operatorname{Spec}(R)$
are injective. Finally, since the prime ideals of
![]() $A^{\operatorname{ic}}$
and
$A^{\operatorname{ic}}$
and
![]() $R$
are totally ordered, the bijection
$R$
are totally ordered, the bijection
![]() $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)$
is a homeomorphism.◻
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A)$
is a homeomorphism.◻
Lemma 17. Suppose that
![]() $R$
is a hvr of characteristic
$R$
is a hvr of characteristic
![]() $p$
with fraction field
$p$
with fraction field
![]() $K$
, and suppose that
$K$
, and suppose that
![]() $K\rightarrow K^{\prime }$
is a purely inseparable extension, and
$K\rightarrow K^{\prime }$
is a purely inseparable extension, and
![]() $R^{\prime }$
the integral closure of
$R^{\prime }$
the integral closure of
![]() $R$
in
$R$
in
![]() $K^{\prime }$
. Then
$K^{\prime }$
. Then
![]() $\operatorname{Spec}(R^{\prime })\rightarrow \operatorname{Spec}(R)$
is a universal homeomorphism.
$\operatorname{Spec}(R^{\prime })\rightarrow \operatorname{Spec}(R)$
is a universal homeomorphism.
Proof. The extension
![]() $R\rightarrow R^{\prime }$
is integral by definition, and
$R\rightarrow R^{\prime }$
is integral by definition, and
![]() $\operatorname{Spec}(R^{\prime })\rightarrow \operatorname{Spec}(R)$
is surjective as it is dominant and satisfies the going up property. So it remains to see that it is injective, and each extension of residue fields is purely inseparable. As
$\operatorname{Spec}(R^{\prime })\rightarrow \operatorname{Spec}(R)$
is surjective as it is dominant and satisfies the going up property. So it remains to see that it is injective, and each extension of residue fields is purely inseparable. As
![]() $R$
is Henselian,
$R$
is Henselian,
![]() $R^{\prime }$
is a valuation ring, and so its poset of primes is totally ordered. By the incomparability property, it follows that there is exactly one prime of
$R^{\prime }$
is a valuation ring, and so its poset of primes is totally ordered. By the incomparability property, it follows that there is exactly one prime of
![]() $R^{\prime }$
lying over any prime of
$R^{\prime }$
lying over any prime of
![]() $R$
. Let
$R$
. Let
![]() $\mathfrak{p}\subset R$
be a prime and
$\mathfrak{p}\subset R$
be a prime and
![]() $\mathfrak{p}^{\prime }\subset R^{\prime }$
the prime lying over it. Localizing at
$\mathfrak{p}^{\prime }\subset R^{\prime }$
the prime lying over it. Localizing at
![]() $\mathfrak{p}$
we can assume both are maximal ideals. Then a given
$\mathfrak{p}$
we can assume both are maximal ideals. Then a given
![]() $a\in k(\mathfrak{p}^{\prime })=R^{\prime }/\mathfrak{p}^{\prime }$
, lifts to some
$a\in k(\mathfrak{p}^{\prime })=R^{\prime }/\mathfrak{p}^{\prime }$
, lifts to some
![]() $b\in R^{\prime }$
, and since
$b\in R^{\prime }$
, and since
![]() $K^{\prime }/K$
is purely inseparable,
$K^{\prime }/K$
is purely inseparable,
![]() $b^{p^{i}}\in K$
for some
$b^{p^{i}}\in K$
for some
![]() $i$
. Now
$i$
. Now
![]() $R^{\prime }$
is the integral closure of
$R^{\prime }$
is the integral closure of
![]() $R$
in
$R$
in
![]() $K^{\prime }$
, so
$K^{\prime }$
, so
![]() $b$
satisfies some monic
$b$
satisfies some monic
![]() $f(T)\in R[T]$
. But then
$f(T)\in R[T]$
. But then
![]() $b^{p^{i}}$
satisfies the monic
$b^{p^{i}}$
satisfies the monic
![]() $f(T)^{p^{i}}$
. Since valuation rings are normal, it follows that
$f(T)^{p^{i}}$
. Since valuation rings are normal, it follows that
![]() $b^{p^{i}}\in R$
. Consequently,
$b^{p^{i}}\in R$
. Consequently,
![]() $a^{p^{i}}\in k(\mathfrak{p})=R/\mathfrak{p}$
. So
$a^{p^{i}}\in k(\mathfrak{p})=R/\mathfrak{p}$
. So
![]() $k(\mathfrak{p}^{\prime })/k(\mathfrak{p})$
is purely inseparable.◻
$k(\mathfrak{p}^{\prime })/k(\mathfrak{p})$
is purely inseparable.◻
5 Pseudo-normalization
One of the obstacles to using valuation rings to study finite type morphisms of Noetherian schemes is non-Nagataness: Suppose
![]() $R$
is a hvr and
$R$
is a hvr and
![]() $R\subset A$
a finite extension with
$R\subset A$
a finite extension with
![]() $A$
an integral domain. Then the normalization
$A$
an integral domain. Then the normalization
![]() $\widetilde{A}$
of
$\widetilde{A}$
of
![]() $A$
is a valuation ring, Lemma 16. If
$A$
is a valuation ring, Lemma 16. If
![]() $\operatorname{Frac}(A)/\operatorname{Frac}(R)$
is finite separable and
$\operatorname{Frac}(A)/\operatorname{Frac}(R)$
is finite separable and
![]() $R$
is discrete then the morphism
$R$
is discrete then the morphism
![]() $R\rightarrow \widetilde{A}$
is also finite [Reference BourbakiBou64, Chapter 6, Section 8, No. 5, Theorem 2, Corollary 1]. However, in general, the morphism
$R\rightarrow \widetilde{A}$
is also finite [Reference BourbakiBou64, Chapter 6, Section 8, No. 5, Theorem 2, Corollary 1]. However, in general, the morphism
![]() $R\rightarrow \widetilde{A}$
may not be finite.
$R\rightarrow \widetilde{A}$
may not be finite.
Example 18. [Reference BourbakiBou64, Chapter 6, Section 8, Exercise 3b]
Let
![]() $k=\mathbb{F}_{p}(X_{n})_{n\in \mathbb{N}}$
, and equip
$k=\mathbb{F}_{p}(X_{n})_{n\in \mathbb{N}}$
, and equip
![]() $K=k(U,V)$
, with the (discrete) valuation induced by
$K=k(U,V)$
, with the (discrete) valuation induced by
![]() $\unicode[STIX]{x1D719}:k(U,V)\rightarrow k((U));V\mapsto \sum _{i=0}^{\infty }X_{i}^{p}U^{ip}$
. Let
$\unicode[STIX]{x1D719}:k(U,V)\rightarrow k((U));V\mapsto \sum _{i=0}^{\infty }X_{i}^{p}U^{ip}$
. Let
![]() $K^{\prime }=K(V^{1/p})$
. Then, (exercise), the unique extension of valued fields
$K^{\prime }=K(V^{1/p})$
. Then, (exercise), the unique extension of valued fields
![]() $K^{\prime }/K$
induces an isomorphism on both value groups and residue fields. Consequently, the corresponding morphism
$K^{\prime }/K$
induces an isomorphism on both value groups and residue fields. Consequently, the corresponding morphism
![]() $R\rightarrow R^{\prime }$
of discrete valuation rings is not finite, and so the normalization
$R\rightarrow R^{\prime }$
of discrete valuation rings is not finite, and so the normalization
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $R[V^{1/p}]$
is not finite over
$R[V^{1/p}]$
is not finite over
![]() $R[V^{1/p}]$
.
$R[V^{1/p}]$
.
On the other hand, at least if the rank of
![]() $R$
is finite, if we take a large enough member
$R$
is finite, if we take a large enough member
![]() $\breve{A}$
of the filtered poset of finitely generated sub-
$\breve{A}$
of the filtered poset of finitely generated sub-
![]() $A$
-algebras of
$A$
-algebras of
![]() $\widetilde{A}$
, the induced morphism
$\widetilde{A}$
, the induced morphism
![]() $\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(\breve{A})$
will be a universal homeomorphism (and even completely decomposed). Hence, as far as
$\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(\breve{A})$
will be a universal homeomorphism (and even completely decomposed). Hence, as far as
![]() $\operatorname{uh}$
-sheaves (and even
$\operatorname{uh}$
-sheaves (and even
![]() $\operatorname{cdh}$
-sheaves, cf. [Reference Huber and KellyHK18, Lemma 2.9]) are concerned, the normalization might as well be finite.
$\operatorname{cdh}$
-sheaves, cf. [Reference Huber and KellyHK18, Lemma 2.9]) are concerned, the normalization might as well be finite.
To formalize this phenomenon, we introduce the notions of pseudo-integral closure, pseudo-normalization, and pseudo-hvr.
Convention. [EGAII, Corollary 6.3.8], [Stacks, Tag. 035N, 035P] . By normalization
![]() $\widetilde{A}$
of a ring
$\widetilde{A}$
of a ring
![]() $A$
with finitely many minimal primes, we mean the integral closure of its associated reduced ring
$A$
with finitely many minimal primes, we mean the integral closure of its associated reduced ring
![]() $A^{\operatorname{red}}$
in the total ring of fractions of
$A^{\operatorname{red}}$
in the total ring of fractions of
![]() $Q(A^{\operatorname{red}})$
of
$Q(A^{\operatorname{red}})$
of
![]() $A^{\operatorname{red}}$
.
$A^{\operatorname{red}}$
.
Note, that usually one only talks of normalizations of reduced rings.
Definition 19. Let
![]() $A$
be a ring and
$A$
be a ring and
![]() $A\rightarrow B$
an
$A\rightarrow B$
an
![]() $A$
-algebra. Define a pseudo-integral closure of
$A$
-algebra. Define a pseudo-integral closure of
![]() $A$
in
$A$
in
![]() $B$
to be a finite sub-
$B$
to be a finite sub-
![]() $A$
-algebra
$A$
-algebra
![]() $A\rightarrow B^{\operatorname{pic}}\subseteq B^{\operatorname{ic}}$
of the integral closure
$A\rightarrow B^{\operatorname{pic}}\subseteq B^{\operatorname{ic}}$
of the integral closure
![]() $B^{ic}\subseteq B$
of
$B^{ic}\subseteq B$
of
![]() $A$
in
$A$
in
![]() $B$
such that
$B$
such that
![]() $\operatorname{Spec}(B^{\operatorname{pic}})\rightarrow \operatorname{Spec}(B^{\operatorname{ic}})$
is a completely decomposed universal homeomorphism.
$\operatorname{Spec}(B^{\operatorname{pic}})\rightarrow \operatorname{Spec}(B^{\operatorname{ic}})$
is a completely decomposed universal homeomorphism.
A pseudo-normalization of a ring
![]() $A$
with finitely many minimal primes is a pseudo-integral closure of
$A$
with finitely many minimal primes is a pseudo-integral closure of
![]() $A$
in its normalization
$A$
in its normalization
![]() $A\rightarrow \breve{A}\subseteq (A^{\operatorname{red}})^{{\sim}}$
. We will write
$A\rightarrow \breve{A}\subseteq (A^{\operatorname{red}})^{{\sim}}$
. We will write
![]() $\mathsf{PseIntClo}(B/A)$
and
$\mathsf{PseIntClo}(B/A)$
and
![]() $\mathsf{PseNor}(A)$
for the set of pseudo-integral closures, and pseudo-normalizations respectively.
$\mathsf{PseNor}(A)$
for the set of pseudo-integral closures, and pseudo-normalizations respectively.
A pseudo-hvr is an integral domain
![]() $A$
such that
$A$
such that
![]() $\widetilde{A}$
is an hvr, and
$\widetilde{A}$
is an hvr, and
![]() $A$
is a pseudo-normalization of itself,
$A$
is a pseudo-normalization of itself,
![]() $A=\breve{A}$
. That is,
$A=\breve{A}$
. That is,
![]() $\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(A)$
is a completely decomposed universal homeomorphism.
$\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(A)$
is a completely decomposed universal homeomorphism.
Even if pseudo-integral closures and pseudo-normalizations exist they are certainly not unique in general. If the normalization, respectively, integral closure is finite, then it is the final pseudo-normalization, respectively, pseudo-integral closure.
The following lemma contains the basic facts we need about pseudo-normalizations
![]() $\breve{A}$
, at least for finite rings
$\breve{A}$
, at least for finite rings
![]() $A$
over a finite rank hvr
$A$
over a finite rank hvr
![]() $R$
: (3) they exist, (2), (4) they are (ind-)functorial for dominant morphisms, and (5) they preserve flat morphisms.
$R$
: (3) they exist, (2), (4) they are (ind-)functorial for dominant morphisms, and (5) they preserve flat morphisms.
Lemma 20. Let
![]() $R$
be a finite rank hvr.
$R$
be a finite rank hvr.
(1) Let
 $A\rightarrow B$
be a ring homomorphism. If
$A\rightarrow B$
be a ring homomorphism. If
 $B^{\operatorname{pic}}\subseteq B^{\operatorname{ic}}$
is a pseudo-integral closure, then any finitely generated subalgebra
$B^{\operatorname{pic}}\subseteq B^{\operatorname{ic}}$
is a pseudo-integral closure, then any finitely generated subalgebra
 $B^{\operatorname{pic}}\subseteq B^{\prime }\subseteq B^{\operatorname{ic}}$
is also a pseudo-integral closure.
$B^{\operatorname{pic}}\subseteq B^{\prime }\subseteq B^{\operatorname{ic}}$
is also a pseudo-integral closure.(2) If the collection of pseudo-integral closures of a ring homomorphism
 $A\rightarrow B$
is nonempty, then it is a filtered poset and
$A\rightarrow B$
is nonempty, then it is a filtered poset and
 $B^{\operatorname{ic}}=\bigcup _{B^{\operatorname{pic}}\in \mathsf{PseIntClo}(B/A)}B^{\operatorname{pic}}$
.
$B^{\operatorname{ic}}=\bigcup _{B^{\operatorname{pic}}\in \mathsf{PseIntClo}(B/A)}B^{\operatorname{pic}}$
.(3) If
 $A$
is a finite
$A$
is a finite
 $R$
-algebra, and
$R$
-algebra, and
 $Q(A^{\operatorname{red}})\rightarrow K$
finite with
$Q(A^{\operatorname{red}})\rightarrow K$
finite with
 $K$
reduced, the poset
$K$
reduced, the poset
 $\mathsf{PseIntClo}(K/A)$
of pseudo-integral closures is nonempty. In particular, the conclusion of part (2) holds.
$\mathsf{PseIntClo}(K/A)$
of pseudo-integral closures is nonempty. In particular, the conclusion of part (2) holds.(4) If
 $\unicode[STIX]{x1D719}:A\rightarrow B$
is a morphism of finite
$\unicode[STIX]{x1D719}:A\rightarrow B$
is a morphism of finite
 $R$
-algebras such that
$R$
-algebras such that
 $\operatorname{Spec}(\unicode[STIX]{x1D719})$
sends generic points to generic points, anda square of finite morphisms of reduced rings, then for any
$\operatorname{Spec}(\unicode[STIX]{x1D719})$
sends generic points to generic points, anda square of finite morphisms of reduced rings, then for any
 $A^{\operatorname{pic}}\in \mathsf{PseIntClo}(K/A)$
there is a
$A^{\operatorname{pic}}\in \mathsf{PseIntClo}(K/A)$
there is a
 $B^{\operatorname{pic}}\in \mathsf{PseIntClo}(L/B)$
compatible with the above square. In other words, the canonical morphism of integral closures
$B^{\operatorname{pic}}\in \mathsf{PseIntClo}(L/B)$
compatible with the above square. In other words, the canonical morphism of integral closures
 $A^{\operatorname{ic}}\rightarrow B^{\operatorname{ic}}$
of
$A^{\operatorname{ic}}\rightarrow B^{\operatorname{ic}}$
of
 $A\rightarrow B$
in
$A\rightarrow B$
in
 $K\rightarrow L$
induces a morphism of ind-objects
$K\rightarrow L$
induces a morphism of ind-objects 
(5) If
 $\unicode[STIX]{x1D719}:A\rightarrow B$
is a finite flat morphism of finite
$\unicode[STIX]{x1D719}:A\rightarrow B$
is a finite flat morphism of finite
 $R$
-algebras, then there exists an inclusion
$R$
-algebras, then there exists an inclusion
 $\breve{A}\subseteq \breve{B}$
of pseudo-normalizations compatible with
$\breve{A}\subseteq \breve{B}$
of pseudo-normalizations compatible with
 $\unicode[STIX]{x1D719}$
, which is flat.
$\unicode[STIX]{x1D719}$
, which is flat.
Proof.
(1) Since
 $B^{\operatorname{ic}}\supseteq B^{\operatorname{pic}}$
is integral so is
$B^{\operatorname{ic}}\supseteq B^{\operatorname{pic}}$
is integral so is
 $B^{\operatorname{ic}}\supseteq B^{\prime }$
, and consequently,
$B^{\operatorname{ic}}\supseteq B^{\prime }$
, and consequently,
 $\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\prime })$
is surjective, [Stacks, Tag 00GQ ]. But
$\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\prime })$
is surjective, [Stacks, Tag 00GQ ]. But
 $\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\operatorname{pic}})$
is a homeomorphism, so
$\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\operatorname{pic}})$
is a homeomorphism, so
 $\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\prime })$
is also injective. Finally, for any point
$\operatorname{Spec}(B^{\operatorname{ic}})\rightarrow \operatorname{Spec}(B^{\prime })$
is also injective. Finally, for any point
 $x\in \operatorname{Spec}(B^{\operatorname{ic}})$
with images
$x\in \operatorname{Spec}(B^{\operatorname{ic}})$
with images
 $y,z$
in
$y,z$
in
 $\operatorname{Spec}(B^{\prime }),\operatorname{Spec}(B^{\operatorname{pic}})$
, The isomorphism
$\operatorname{Spec}(B^{\prime }),\operatorname{Spec}(B^{\operatorname{pic}})$
, The isomorphism
 $k(x)\cong k(z)$
implies an isomorphism
$k(x)\cong k(z)$
implies an isomorphism
 $k(x)\cong k(y)$
.
$k(x)\cong k(y)$
.(2) Follows from part (1).
(3) Let
 $A^{\operatorname{ic}}$
be the integral closure of
$A^{\operatorname{ic}}$
be the integral closure of
 $A^{\operatorname{red}}$
in
$A^{\operatorname{red}}$
in
 $K$
. Since
$K$
. Since
 $A^{\operatorname{red}}$
is reduced with finitely many minimal primes,
$A^{\operatorname{red}}$
is reduced with finitely many minimal primes,
 $Q(A^{\operatorname{red}})$
is a finite product of fields, [Stacks, Tag 02LV], so
$Q(A^{\operatorname{red}})$
is a finite product of fields, [Stacks, Tag 02LV], so
 $K$
is also a finite product of fields. Hence
$K$
is also a finite product of fields. Hence
 $A^{\operatorname{ic}}$
is the product of the integral closures in the residue fields of
$A^{\operatorname{ic}}$
is the product of the integral closures in the residue fields of
 $K$
, and therefore it suffices to consider the case
$K$
, and therefore it suffices to consider the case
 $A$
and
$A$
and
 $K$
are both integral domains. Replacing
$K$
are both integral domains. Replacing
 $R$
with its image in
$R$
with its image in
 $A$
, we can also assume
$A$
, we can also assume
 $R\rightarrow A$
is injective. Now
$R\rightarrow A$
is injective. Now
 $R\subseteq A^{\operatorname{ic}}$
is an extension of valuation rings, Lemma 16. As
$R\subseteq A^{\operatorname{ic}}$
is an extension of valuation rings, Lemma 16. As
 $R\subseteq A^{\operatorname{ic}}$
is generically finite, for every prime
$R\subseteq A^{\operatorname{ic}}$
is generically finite, for every prime
 $\mathfrak{p}\subset R$
, the extension
$\mathfrak{p}\subset R$
, the extension
 $k(\mathfrak{p})\subset k(\mathfrak{q})$
is finite, where
$k(\mathfrak{p})\subset k(\mathfrak{q})$
is finite, where
 $\mathfrak{q}\subset A^{\operatorname{ic}}$
is the prime lying over
$\mathfrak{q}\subset A^{\operatorname{ic}}$
is the prime lying over
 $\mathfrak{p}$
, [Stacks, Tag 0ASH]. For each prime of
$\mathfrak{p}$
, [Stacks, Tag 0ASH]. For each prime of
 $R$
, choose a set of generators of the corresponding finite field extension, lift them to
$R$
, choose a set of generators of the corresponding finite field extension, lift them to
 $A$
, and let
$A$
, and let
 $A^{\operatorname{pic}}$
be the sub-
$A^{\operatorname{pic}}$
be the sub-
 $R$
-algebra that they generate. Certainly,
$R$
-algebra that they generate. Certainly,
 $A^{\operatorname{pic}}$
is a finite
$A^{\operatorname{pic}}$
is a finite
 $R$
-algebra. The morphism
$R$
-algebra. The morphism
 $A^{\operatorname{pic}}\subseteq A^{\operatorname{ic}}$
is an integral ring extension so
$A^{\operatorname{pic}}\subseteq A^{\operatorname{ic}}$
is an integral ring extension so
 $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A^{\operatorname{pic}})$
is surjective, [Stacks, Tag 00GQ ]. As
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A^{\operatorname{pic}})$
is surjective, [Stacks, Tag 00GQ ]. As
 $R$
is Henselian,
$R$
is Henselian,
 $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(R)$
is a homeomorphism, and we conclude that
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(R)$
is a homeomorphism, and we conclude that
 $\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A^{\operatorname{pic}})$
is also a homeomorphism. By construction it induces isomorphisms on all field extensions. Hence, it is a completely decomposed universal homeomorphism. So
$\operatorname{Spec}(A^{\operatorname{ic}})\rightarrow \operatorname{Spec}(A^{\operatorname{pic}})$
is also a homeomorphism. By construction it induces isomorphisms on all field extensions. Hence, it is a completely decomposed universal homeomorphism. So
 $\mathsf{PseIntClo}(K/A)$
is nonempty.
$\mathsf{PseIntClo}(K/A)$
is nonempty.(4) This follows from Part (3)—Existence, and Part (1)—Closure under subextension: Choose any
 $B_{0}^{\operatorname{pic}}\in \mathsf{PseIntClo}(B)$
and take
$B_{0}^{\operatorname{pic}}\in \mathsf{PseIntClo}(B)$
and take
 $B^{\operatorname{pic}}$
to be the sub-
$B^{\operatorname{pic}}$
to be the sub-
 $B$
-algebra of
$B$
-algebra of
 $L$
generated by the image of
$L$
generated by the image of
 $A^{\operatorname{pic}}$
and
$A^{\operatorname{pic}}$
and
 $B_{0}^{\operatorname{pic}}$
.
$B_{0}^{\operatorname{pic}}$
.(5) We will construct the following diagram. Note all morphisms except possibly the ones with source
 $A$
and
$A$
and
 $B$
are inclusions.
$B$
are inclusions. 
Given some
 $\breve{A_{1}}\rightarrow \breve{B_{1}}$
extending
$\breve{A_{1}}\rightarrow \breve{B_{1}}$
extending
 $A\rightarrow B$
, consider the sub-
$A\rightarrow B$
, consider the sub-
 $(A^{\operatorname{red}})^{{\sim}}$
-algebra
$(A^{\operatorname{red}})^{{\sim}}$
-algebra
 $\breve{B}_{1}\subseteq B^{\prime }\subseteq (B^{\operatorname{red}})^{{\sim}}$
generated by the image of
$\breve{B}_{1}\subseteq B^{\prime }\subseteq (B^{\operatorname{red}})^{{\sim}}$
generated by the image of
 $\breve{B_{1}}$
. As
$\breve{B_{1}}$
. As
 $(B^{\operatorname{red}})^{{\sim}}$
is
$(B^{\operatorname{red}})^{{\sim}}$
is
 $(A^{\operatorname{red}})^{{\sim}}$
-torsion-free, so is
$(A^{\operatorname{red}})^{{\sim}}$
-torsion-free, so is
 $B^{\prime }$
, and as
$B^{\prime }$
, and as
 $(A^{\operatorname{red}})^{{\sim}}$
is a (product of) valuation rings, Lemma 16, we deduce that
$(A^{\operatorname{red}})^{{\sim}}$
is a (product of) valuation rings, Lemma 16, we deduce that
 $B^{\prime }$
is
$B^{\prime }$
is
 $(A^{\operatorname{red}})^{{\sim}}$
-flat. As
$(A^{\operatorname{red}})^{{\sim}}$
-flat. As
 $\breve{A}_{1}\rightarrow \breve{B}_{1}$
is finite type,
$\breve{A}_{1}\rightarrow \breve{B}_{1}$
is finite type,
 $(A^{\operatorname{red}})^{{\sim}}\rightarrow B^{\prime }$
is also finite type. Since
$(A^{\operatorname{red}})^{{\sim}}\rightarrow B^{\prime }$
is also finite type. Since
 $(A^{\operatorname{red}})^{{\sim}}$
is a product of local rings, the finitely generated flat module
$(A^{\operatorname{red}})^{{\sim}}$
is a product of local rings, the finitely generated flat module
 $B^{\prime }$
is a free module (Noetherianness is not needed, [Reference MatsumuraMat89, Theorem 7.10]). As
$B^{\prime }$
is a free module (Noetherianness is not needed, [Reference MatsumuraMat89, Theorem 7.10]). As
 $(A^{\operatorname{red}})^{{\sim}}=\bigcup _{\mathsf{PseNor}(A)}\breve{A}$
, we haveFootnote
5
$(A^{\operatorname{red}})^{{\sim}}=\bigcup _{\mathsf{PseNor}(A)}\breve{A}$
, we haveFootnote
5
 $B^{\prime }\cong (A^{\operatorname{red}})^{{\sim}}\otimes _{\breve{A_{2}}}\breve{B_{2}}$
for some finite free
$B^{\prime }\cong (A^{\operatorname{red}})^{{\sim}}\otimes _{\breve{A_{2}}}\breve{B_{2}}$
for some finite free
 $\breve{A_{2}}\rightarrow \breve{B_{2}}$
with
$\breve{A_{2}}\rightarrow \breve{B_{2}}$
with
 $\breve{A_{2}}$
in
$\breve{A_{2}}$
in
 $\mathsf{PseNor}(A)$
(the ring
$\mathsf{PseNor}(A)$
(the ring
 $\breve{B_{2}}$
is not necessarily in
$\breve{B_{2}}$
is not necessarily in
 $\mathsf{PseNor}(B)$
yet). Since
$\mathsf{PseNor}(B)$
yet). Since
 $(\bigcup _{\breve{A}\supseteq \breve{A_{2}}\in \mathsf{PseNor}(A)}\breve{A})\otimes _{\breve{A_{2}}}\breve{B_{2}}\cong B^{\prime }\supseteq \breve{B}_{1}$
, tensoring with some large enough
$(\bigcup _{\breve{A}\supseteq \breve{A_{2}}\in \mathsf{PseNor}(A)}\breve{A})\otimes _{\breve{A_{2}}}\breve{B_{2}}\cong B^{\prime }\supseteq \breve{B}_{1}$
, tensoring with some large enough
 $\breve{A}_{3}\supseteq \breve{A}_{2}$
in
$\breve{A}_{3}\supseteq \breve{A}_{2}$
in
 $\mathsf{PseNor}(A)$
, we get our
$\mathsf{PseNor}(A)$
, we get our
 $\breve{B}_{3}\cong \breve{A}_{3}\otimes _{\breve{A}_{2}}\breve{B}_{2}\supseteq \breve{B}_{1}\supseteq \breve{B}_{0}$
, with
$\breve{B}_{3}\cong \breve{A}_{3}\otimes _{\breve{A}_{2}}\breve{B}_{2}\supseteq \breve{B}_{1}\supseteq \breve{B}_{0}$
, with
 $\breve{A}_{3}\rightarrow \breve{B}_{3}$
in
$\breve{A}_{3}\rightarrow \breve{B}_{3}$
in
 $\mathsf{PseNor}(\unicode[STIX]{x1D719})$
. ◻
$\mathsf{PseNor}(\unicode[STIX]{x1D719})$
. ◻
Lemma 21. Let
![]() $R$
be a hvr of characteristic
$R$
be a hvr of characteristic
![]() $p\neq l$
. Then any
$p\neq l$
. Then any
![]() $\operatorname{fps}l^{\prime }$
-morphism
$\operatorname{fps}l^{\prime }$
-morphism
![]() $R\rightarrow A$
is corefinable by the composition of a generically étale
$R\rightarrow A$
is corefinable by the composition of a generically étale
![]() $\operatorname{fps}l^{\prime }$
-morphism
$\operatorname{fps}l^{\prime }$
-morphism
![]() $R\rightarrow A^{\prime }$
and a
$R\rightarrow A^{\prime }$
and a
![]() $\operatorname{uh}$
-morphism
$\operatorname{uh}$
-morphism
![]() $A^{\prime }\rightarrow A^{\prime \prime }$
such that
$A^{\prime }\rightarrow A^{\prime \prime }$
such that
![]() $R\rightarrow A^{\prime \prime }$
is also
$R\rightarrow A^{\prime \prime }$
is also
![]() $\operatorname{fps}l^{\prime }$
.
$\operatorname{fps}l^{\prime }$
.
Proof. First consider the case when
![]() $A$
is an integral domain. Consider the separable closure
$A$
is an integral domain. Consider the separable closure
![]() $L$
of
$L$
of
![]() $\operatorname{Frac}(R)$
in
$\operatorname{Frac}(R)$
in
![]() $\operatorname{Frac}(A)$
, and choose pseudo-integral closures
$\operatorname{Frac}(A)$
, and choose pseudo-integral closures
![]() $A^{\prime },A^{\prime \prime }$
of
$A^{\prime },A^{\prime \prime }$
of
![]() $R,A$
in
$R,A$
in
![]() $L,\operatorname{Frac}(A)$
respectively, Lemma 20(4).
$L,\operatorname{Frac}(A)$
respectively, Lemma 20(4).

By definition,
![]() $A^{\prime }\rightarrow \widetilde{A^{\prime }}$
and
$A^{\prime }\rightarrow \widetilde{A^{\prime }}$
and
![]() $A^{\prime \prime }\rightarrow \widetilde{A^{\prime \prime }}$
induce completely decomposed
$A^{\prime \prime }\rightarrow \widetilde{A^{\prime \prime }}$
induce completely decomposed
![]() $\operatorname{uh}$
-morphisms, and
$\operatorname{uh}$
-morphisms, and
![]() $\widetilde{A^{\prime }}\rightarrow \widetilde{A^{\prime \prime }}$
induces a universal homeomorphism by Lemma 17. Hence
$\widetilde{A^{\prime }}\rightarrow \widetilde{A^{\prime \prime }}$
induces a universal homeomorphism by Lemma 17. Hence
![]() $A^{\prime }\rightarrow A^{\prime \prime }$
is a universal homeomorphism.
$A^{\prime }\rightarrow A^{\prime \prime }$
is a universal homeomorphism.
So now it suffices to show that every
![]() $\operatorname{fps}l^{\prime }$
-morphism
$\operatorname{fps}l^{\prime }$
-morphism
![]() $R\rightarrow A$
is corefinable by an
$R\rightarrow A$
is corefinable by an
![]() $\operatorname{fps}l^{\prime }$
-morphism
$\operatorname{fps}l^{\prime }$
-morphism
![]() $R\rightarrow A^{\prime \prime }$
with
$R\rightarrow A^{\prime \prime }$
with
![]() $A^{\prime \prime }$
an integral domain. Suppose first that
$A^{\prime \prime }$
an integral domain. Suppose first that
![]() $R$
is a field
$R$
is a field
![]() $K=R$
. Then one of the residue fields of
$K=R$
. Then one of the residue fields of
![]() $A$
is of degree prime to
$A$
is of degree prime to
![]() $l$
: Indeed, write
$l$
: Indeed, write
![]() $A=\prod A_{\mathfrak{p}_{i}}$
as the product of its local rings. As
$A=\prod A_{\mathfrak{p}_{i}}$
as the product of its local rings. As
![]() $l\nmid \dim _{K}A$
we have
$l\nmid \dim _{K}A$
we have
![]() $l\nmid \dim _{K}A_{\mathfrak{p}_{i}}$
for some
$l\nmid \dim _{K}A_{\mathfrak{p}_{i}}$
for some
![]() $i$
. As
$i$
. As
![]() $\dim _{K}A_{\mathfrak{p}_{i}}=\sum _{j}\dim _{K}\mathfrak{p}_{i}^{j}/\mathfrak{p}_{i}^{j+1}$
and each
$\dim _{K}A_{\mathfrak{p}_{i}}=\sum _{j}\dim _{K}\mathfrak{p}_{i}^{j}/\mathfrak{p}_{i}^{j+1}$
and each
![]() $\mathfrak{p}_{i}^{j}/\mathfrak{p}_{i}^{j+1}$
is a
$\mathfrak{p}_{i}^{j}/\mathfrak{p}_{i}^{j+1}$
is a
![]() $k(\mathfrak{p}_{j})$
-vector space, we see that
$k(\mathfrak{p}_{j})$
-vector space, we see that
![]() $l\nmid [k(\mathfrak{p}_{i}):K]$
. For a general
$l\nmid [k(\mathfrak{p}_{i}):K]$
. For a general
![]() $R$
, the previous case applied to
$R$
, the previous case applied to
![]() $\operatorname{Frac}(R)\rightarrow \operatorname{Frac}(R)\otimes _{R}A$
produces a minimal prime
$\operatorname{Frac}(R)\rightarrow \operatorname{Frac}(R)\otimes _{R}A$
produces a minimal prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $A$
such that
$A$
such that
![]() $l\nmid [A_{\mathfrak{p}}^{\operatorname{red}}:\operatorname{Frac}(R)]$
. But then since flat
$l\nmid [A_{\mathfrak{p}}^{\operatorname{red}}:\operatorname{Frac}(R)]$
. But then since flat
![]() $=$
torsion-free over valuation rings,
$=$
torsion-free over valuation rings,
![]() $R\rightarrow A/\mathfrak{p}$
is
$R\rightarrow A/\mathfrak{p}$
is
![]() $\operatorname{fps}l^{\prime }$
.◻
$\operatorname{fps}l^{\prime }$
.◻
Lemma 22. If
![]() $R$
is a finite rank hvr and
$R$
is a finite rank hvr and
![]() $R\rightarrow A$
a finite
$R\rightarrow A$
a finite
![]() $R$
-algebra, then every
$R$
-algebra, then every
![]() $l\operatorname{dh}$
-cover of
$l\operatorname{dh}$
-cover of
![]() $\operatorname{Spec}(A)$
is refinable by a finite one.
$\operatorname{Spec}(A)$
is refinable by a finite one.
Proof. Since every
![]() $l\operatorname{dh}$
-covering is refinable by the composition of an
$l\operatorname{dh}$
-covering is refinable by the composition of an
![]() $\operatorname{fps}l^{\prime }$
-covering and a
$\operatorname{fps}l^{\prime }$
-covering and a
![]() $\operatorname{cdh}$
-covering (see the proof of B.5(4)) it suffices to prove the statement for
$\operatorname{cdh}$
-covering (see the proof of B.5(4)) it suffices to prove the statement for
![]() $\operatorname{cdh}$
-coverings. Replacing
$\operatorname{cdh}$
-coverings. Replacing
![]() $A$
with
$A$
with
![]() $\prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}\text{ prime}}}(A/\mathfrak{p})^{\smallsmile }$
we can assume that
$\prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}\text{ prime}}}(A/\mathfrak{p})^{\smallsmile }$
we can assume that
![]() $A$
is a pseudo-hvr. That is,
$A$
is a pseudo-hvr. That is,
![]() $\widetilde{A}$
is a hvr and
$\widetilde{A}$
is a hvr and
![]() $\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(A)$
is a completely decomposed universal homeomorphism. Let
$\operatorname{Spec}(\widetilde{A})\rightarrow \operatorname{Spec}(A)$
is a completely decomposed universal homeomorphism. Let
![]() $\operatorname{Spec}(B)\rightarrow \operatorname{Spec}(A)$
be the
$\operatorname{Spec}(B)\rightarrow \operatorname{Spec}(A)$
be the
![]() $\operatorname{cdh}$
-covering in question, which we assume is affine, and since our
$\operatorname{cdh}$
-covering in question, which we assume is affine, and since our
![]() $\operatorname{cdh}$
-topology is pulled back from a Noetherian scheme (cf. Proposition B.4), we also assume its of finite presentation
$\operatorname{cdh}$
-topology is pulled back from a Noetherian scheme (cf. Proposition B.4), we also assume its of finite presentation
![]() $B\cong A[x_{1},\ldots ,x_{n}]/\langle f_{1},\ldots ,f_{m}\rangle$
. Every
$B\cong A[x_{1},\ldots ,x_{n}]/\langle f_{1},\ldots ,f_{m}\rangle$
. Every
![]() $\operatorname{cdh}$
-covering of a hvr admits a section, so there is a factorization
$\operatorname{cdh}$
-covering of a hvr admits a section, so there is a factorization
![]() $A\rightarrow B\rightarrow \widetilde{A}$
. As
$A\rightarrow B\rightarrow \widetilde{A}$
. As
![]() $A\rightarrow \widetilde{A}$
is an integral extension, the images of the
$A\rightarrow \widetilde{A}$
is an integral extension, the images of the
![]() $x_{i}$
in
$x_{i}$
in
![]() $\widetilde{A}$
satisfy some monic polynomials
$\widetilde{A}$
satisfy some monic polynomials
![]() $g_{i}(T)\in A[T]$
. Then the composition
$g_{i}(T)\in A[T]$
. Then the composition
![]() $A\rightarrow B\rightarrow B^{\prime }:=A[x_{1},\ldots ,x_{n}]\langle f_{1},\ldots ,f_{m},g_{1}(x_{1}),\ldots ,g_{n}(x_{n})\rangle$
is a finite morphism, and its
$A\rightarrow B\rightarrow B^{\prime }:=A[x_{1},\ldots ,x_{n}]\langle f_{1},\ldots ,f_{m},g_{1}(x_{1}),\ldots ,g_{n}(x_{n})\rangle$
is a finite morphism, and its
![]() $\operatorname{Spec}$
is completely decomposed because
$\operatorname{Spec}$
is completely decomposed because
![]() $\operatorname{Spec}$
of the composition
$\operatorname{Spec}$
of the composition
![]() $A\rightarrow B^{\prime }\rightarrow \widetilde{A}$
is completely decomposed.◻
$A\rightarrow B^{\prime }\rightarrow \widetilde{A}$
is completely decomposed.◻
6
 $l\operatorname{dh}$
-descent for pseudo-hvrs
$l\operatorname{dh}$
-descent for pseudo-hvrs
From this point we start working with the following “Gestern” condition. A presheaf
![]() $F$
satisfies (G1) if:
$F$
satisfies (G1) if:
(G1) For every hvr
 $R$
, the canonical morphism
$R$
, the canonical morphism
 $F(R)\rightarrow F(\operatorname{Frac}(R))$
is a monomorphism.
$F(R)\rightarrow F(\operatorname{Frac}(R))$
is a monomorphism.
Remark 23. We find it disappointing that we do not know a proof avoiding this condition, as its not really clear heuristically why it should be involved in passing traces from
![]() $F$
to
$F$
to
![]() $F_{l\operatorname{dh}}$
.
$F_{l\operatorname{dh}}$
.
Voevodsky shows in [Reference VoevodskyVoe00b, Corollary 4.18] that for a homotopy invariant presheaf with transfers
![]() $F$
and a smooth semilocal
$F$
and a smooth semilocal
![]() $k$
-scheme
$k$
-scheme
![]() $X$
, the morphism
$X$
, the morphism
![]() $F(X)\rightarrow F(\unicode[STIX]{x1D702})$
to the generic scheme
$F(X)\rightarrow F(\unicode[STIX]{x1D702})$
to the generic scheme
![]() $\unicode[STIX]{x1D702}$
is a monomorphism. So, at least in the homotopy invariant setting over a field, traces imply a version of (G1). However, in our setting we do not have this: if
$\unicode[STIX]{x1D702}$
is a monomorphism. So, at least in the homotopy invariant setting over a field, traces imply a version of (G1). However, in our setting we do not have this: if
![]() $S$
is a Noetherian base scheme of dimension
$S$
is a Noetherian base scheme of dimension
![]() ${>}0$
,
${>}0$
,
![]() $s$
a nongeneric point, and
$s$
a nongeneric point, and
![]() $F$
the constant additive sheaf of some nontrivial abelian group
$F$
the constant additive sheaf of some nontrivial abelian group
![]() $A$
, then
$A$
, then
![]() $F(-\times _{S}s)$
is clearly
$F(-\times _{S}s)$
is clearly
![]() $\operatorname{uh}$
-invariant, and has traces by Example 14(1), however, will not satisfy (G1).
$\operatorname{uh}$
-invariant, and has traces by Example 14(1), however, will not satisfy (G1).
Proposition 24. Suppose that
![]() $F$
is a
$F$
is a
![]() $\operatorname{uh}$
-invariant
$\operatorname{uh}$
-invariant
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1). Then for any pseudo-hvr
$\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1). Then for any pseudo-hvr
![]() $R$
of positive characteristic
$R$
of positive characteristic
![]() $p\neq l$
, we have
$p\neq l$
, we have
![]() $F(R)=F_{l\operatorname{dh}}(R)$
.
$F(R)=F_{l\operatorname{dh}}(R)$
.
Proof. Since
![]() $F$
is
$F$
is
![]() $\operatorname{uh}$
-invariant, so is
$\operatorname{uh}$
-invariant, so is
![]() $F_{l\operatorname{dh}}$
, Corollary 11, so we can assume
$F_{l\operatorname{dh}}$
, Corollary 11, so we can assume
![]() $R$
is a hvr.
$R$
is a hvr.
Injectivity:
![]() $s\in \ker (F(R)\rightarrow F_{l\operatorname{dh}}(R))$
if and only if there is some
$s\in \ker (F(R)\rightarrow F_{l\operatorname{dh}}(R))$
if and only if there is some
![]() $l\operatorname{dh}$
-covering
$l\operatorname{dh}$
-covering
![]() $f:Y\rightarrow \operatorname{Spec}(R)$
such that
$f:Y\rightarrow \operatorname{Spec}(R)$
such that
![]() $F(f)s=0$
. Since
$F(f)s=0$
. Since
![]() $R$
is a hvr we can assume that
$R$
is a hvr we can assume that
![]() $f$
is an
$f$
is an
![]() $\operatorname{fps}l^{\prime }$
-morphism, Proposition B.5(4). But then
$\operatorname{fps}l^{\prime }$
-morphism, Proposition B.5(4). But then
![]() $s\stackrel{(\text{Deg})}{=}(1/\deg f)\operatorname{Tr}_{f}F(f)s=0$
.
$s\stackrel{(\text{Deg})}{=}(1/\deg f)\operatorname{Tr}_{f}F(f)s=0$
.
Surjectivity: For every
![]() $s\in F_{l\operatorname{dh}}(R)$
there is an
$s\in F_{l\operatorname{dh}}(R)$
there is an
![]() $l\operatorname{dh}$
-covering
$l\operatorname{dh}$
-covering
![]() $f:Y\rightarrow \operatorname{Spec}(R)=:X$
such that
$f:Y\rightarrow \operatorname{Spec}(R)=:X$
such that
![]() $s|_{Y}\in \operatorname{im}(F(Y)\rightarrow F_{l\operatorname{dh}}(Y))$
. Since
$s|_{Y}\in \operatorname{im}(F(Y)\rightarrow F_{l\operatorname{dh}}(Y))$
. Since
![]() $R$
is a hvr we can assume that
$R$
is a hvr we can assume that
![]() $f$
is an
$f$
is an
![]() $\operatorname{fps}l^{\prime }$
-morphism, Proposition B.5(4). In fact, we can assume
$\operatorname{fps}l^{\prime }$
-morphism, Proposition B.5(4). In fact, we can assume
![]() $f$
factors as
$f$
factors as
![]() $Z_{0}\stackrel{f_{1}}{\rightarrow }Y_{0}\stackrel{f_{0}}{\rightarrow }X$
with
$Z_{0}\stackrel{f_{1}}{\rightarrow }Y_{0}\stackrel{f_{0}}{\rightarrow }X$
with
![]() $f_{1}$
a
$f_{1}$
a
![]() $\operatorname{uh}$
-morphism, and
$\operatorname{uh}$
-morphism, and
![]() $f_{0}$
a generically étale
$f_{0}$
a generically étale
![]() $\operatorname{fps}l^{\prime }$
-morphism, Lemma 21. Since
$\operatorname{fps}l^{\prime }$
-morphism, Lemma 21. Since
![]() $F$
is
$F$
is
![]() $\operatorname{uh}$
-invariant, so is
$\operatorname{uh}$
-invariant, so is
![]() $F_{l\operatorname{dh}}$
, Corollary 11, so we can forget
$F_{l\operatorname{dh}}$
, Corollary 11, so we can forget
![]() $f_{1}$
and just work with
$f_{1}$
and just work with
![]() $f_{0}$
. Since
$f_{0}$
. Since
![]() $f_{0}$
is generically étale,
$f_{0}$
is generically étale,
![]() $Y_{0}\times _{X}Y_{0}$
is generically reduced. Choose
$Y_{0}\times _{X}Y_{0}$
is generically reduced. Choose
![]() $Y_{1}=(Y_{0}\times _{X}Y_{0})^{\smallsmile }$
such that the composition
$Y_{1}=(Y_{0}\times _{X}Y_{0})^{\smallsmile }$
such that the composition
![]() $\unicode[STIX]{x1D70B}_{1}:Y_{1}\rightarrow Y_{0}\times _{X}Y_{0}\stackrel{pr_{1}}{\rightarrow }Y_{0}$
is still flat, Lemma 20(5), and therefore
$\unicode[STIX]{x1D70B}_{1}:Y_{1}\rightarrow Y_{0}\times _{X}Y_{0}\stackrel{pr_{1}}{\rightarrow }Y_{0}$
is still flat, Lemma 20(5), and therefore
![]() $\operatorname{fps}l^{\prime }$
. We claim that
$\operatorname{fps}l^{\prime }$
. We claim that
is exact where
![]() $\unicode[STIX]{x1D70B}_{2}$
is the composition
$\unicode[STIX]{x1D70B}_{2}$
is the composition
![]() $Y_{1}\rightarrow Y_{0}\times _{X}Y_{0}\stackrel{pr_{2}}{\rightarrow }Y_{0}$
. Indeed, by
$Y_{1}\rightarrow Y_{0}\times _{X}Y_{0}\stackrel{pr_{2}}{\rightarrow }Y_{0}$
. Indeed, by
![]() $\operatorname{id}\stackrel{(\text{Deg})}{=}(1/\deg f_{0})\operatorname{Tr}_{f_{0}}F(f_{0})$
it is exact at
$\operatorname{id}\stackrel{(\text{Deg})}{=}(1/\deg f_{0})\operatorname{Tr}_{f_{0}}F(f_{0})$
it is exact at
![]() $F(X)$
. For exactness at
$F(X)$
. For exactness at
![]() $F(Y_{0})$
, we claim that
$F(Y_{0})$
, we claim that
![]() $\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})=F(f_{0})\operatorname{Tr}_{f_{0}}$
. Indeed, since
$\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})=F(f_{0})\operatorname{Tr}_{f_{0}}$
. Indeed, since
![]() $Y_{1}$
is
$Y_{1}$
is
![]() $\operatorname{Spec}$
of a (product of) pseudo-hvrs, and
$\operatorname{Spec}$
of a (product of) pseudo-hvrs, and
![]() $F$
is
$F$
is
![]() $\operatorname{uh}$
-invariant, by (G1) it suffices to check this after pulling back to the generic points of
$\operatorname{uh}$
-invariant, by (G1) it suffices to check this after pulling back to the generic points of
![]() $Y_{1}$
. But by (CdB), it suffices to show
$Y_{1}$
. But by (CdB), it suffices to show
![]() $\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})=F(f_{0})\operatorname{Tr}_{f_{0}}$
holds generically, that is, over the generic point
$\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})=F(f_{0})\operatorname{Tr}_{f_{0}}$
holds generically, that is, over the generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $X$
. But
$X$
. But

is cartesian, so the claim follows from (CdB). Hence, the above sequence is exact at
![]() $F(Y_{0})$
since if
$F(Y_{0})$
since if
![]() $F(\unicode[STIX]{x1D70B}_{2})s^{\prime }=F(\unicode[STIX]{x1D70B}_{1})s^{\prime }$
, then
$F(\unicode[STIX]{x1D70B}_{2})s^{\prime }=F(\unicode[STIX]{x1D70B}_{1})s^{\prime }$
, then
![]() $s^{\prime }\stackrel{\text{(Deg)}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{1})s^{\prime }\stackrel{\text{cycle}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})s^{\prime }\stackrel{\text{(“CdB”)}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})F(f_{0})\operatorname{Tr}_{f_{0}}s^{\prime }$
.
$s^{\prime }\stackrel{\text{(Deg)}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{1})s^{\prime }\stackrel{\text{cycle}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1}}F(\unicode[STIX]{x1D70B}_{2})s^{\prime }\stackrel{\text{(“CdB”)}}{=}(1/\deg \unicode[STIX]{x1D70B}_{1})F(f_{0})\operatorname{Tr}_{f_{0}}s^{\prime }$
.
So we have established that the top row in the following diagram is exact. Injectivity for pseudo-hvrs says the right vertical morphism is injective. Hence, by diagram chase, we find a preimage of
![]() $s$
in
$s$
in
![]() $F(X)$
.
$F(X)$
.

7 Traces on
 $F_{l\operatorname{dh}}$
$F_{l\operatorname{dh}}$
In this section, we show that for a nice presheaf with traces
![]() $F$
, the associated
$F$
, the associated
![]() $l\operatorname{dh}$
-sheaf also has traces. We essentially transplant the method of [Reference KellyKel12, Theorem 3.5.5], which becomes much easier in the context of this paper. For another approach to putting trace morphisms on
$l\operatorname{dh}$
-sheaf also has traces. We essentially transplant the method of [Reference KellyKel12, Theorem 3.5.5], which becomes much easier in the context of this paper. For another approach to putting trace morphisms on
![]() $F_{l\operatorname{dh}}$
(with more restrictive hypotheses than we use here) see [Reference KellyKel17].
$F_{l\operatorname{dh}}$
(with more restrictive hypotheses than we use here) see [Reference KellyKel17].
Recall that in [Reference KellyKel12, § 3.5] we defined
for
![]() $F$
a presheaf and
$F$
a presheaf and
![]() $X$
a scheme.
$X$
a scheme.
Remark 25. One sees directly that
![]() $F_{\operatorname{cdd}}$
is a
$F_{\operatorname{cdd}}$
is a
![]() $\operatorname{cdh}$
-sheaf. More specifically, for any completely decomposed morphism
$\operatorname{cdh}$
-sheaf. More specifically, for any completely decomposed morphism
![]() $Y\rightarrow X$
, the sequence
$Y\rightarrow X$
, the sequence
is exact (showing this by hand using a splitting of
![]() $\amalg _{y\in Y}y\rightarrow \amalg _{x\in X}x$
is an easy exercise).
$\amalg _{y\in Y}y\rightarrow \amalg _{x\in X}x$
is an easy exercise).
What takes a little bit more work is the following theorem.
Proposition 26. [Reference KellyKel12, Theorem 3.5.5, Lemma 3.3.6(2), Definition 3.3.4, Proposition 3.5.7]
Let
![]() $F$
be a
$F$
be a
![]() $\operatorname{uh}$
-invariant
$\operatorname{uh}$
-invariant
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces, where
$\mathbb{Z}_{(l)}$
-linear presheaf with traces, where
![]() $l\neq \operatorname{char}s$
for all points
$l\neq \operatorname{char}s$
for all points
![]() $s\in S$
of the base scheme. Then there is a unique structure of traces on
$s\in S$
of the base scheme. Then there is a unique structure of traces on
![]() $F_{\operatorname{cdd}}$
such that
$F_{\operatorname{cdd}}$
such that
![]() $F\rightarrow F_{\operatorname{cdd}}$
is a morphism of presheaves with traces. Moreover, the trace morphisms on
$F\rightarrow F_{\operatorname{cdd}}$
is a morphism of presheaves with traces. Moreover, the trace morphisms on
![]() $F_{\operatorname{cdd}}$
satisfy:
$F_{\operatorname{cdd}}$
satisfy:
- (Tr)
If
 $A$
is a pseudo-hvr,
$A$
is a pseudo-hvr,
 $\unicode[STIX]{x1D719}:A\rightarrow B$
an
$\unicode[STIX]{x1D719}:A\rightarrow B$
an
 $\operatorname{fps}$
morphism,
$\operatorname{fps}$
morphism,
 $\mathfrak{p}_{1},\ldots ,\mathfrak{p}_{n}$
are the minimal ideals of
$\mathfrak{p}_{1},\ldots ,\mathfrak{p}_{n}$
are the minimal ideals of
 $B$
, and
$B$
, and
 $\unicode[STIX]{x1D702}_{i}:B\rightarrow (B/\mathfrak{p}_{i})^{\smallsmile }$
the canonical morphisms, then
$\unicode[STIX]{x1D702}_{i}:B\rightarrow (B/\mathfrak{p}_{i})^{\smallsmile }$
the canonical morphisms, then
where
 $m_{i}=\operatorname{length}~B_{\mathfrak{p}_{i}}$
, and of course,
$m_{i}=\operatorname{length}~B_{\mathfrak{p}_{i}}$
, and of course,
 $(B/\mathfrak{p}_{i})^{\smallsmile }$
are chosen to be flat over
$(B/\mathfrak{p}_{i})^{\smallsmile }$
are chosen to be flat over
 $A$
, (or some
$A$
, (or some
 $\operatorname{cduh}$
-extension of it, and we implicitly use
$\operatorname{cduh}$
-extension of it, and we implicitly use
 $\operatorname{uh}$
-invariance), Lemma 20(5).
$\operatorname{uh}$
-invariance), Lemma 20(5).
Remark 27. We do not need the following description, but in case the reader is interested, we recall that the trace morphisms on
![]() $F_{\operatorname{cdd}}$
are defined as follows. Given an
$F_{\operatorname{cdd}}$
are defined as follows. Given an
![]() $\operatorname{fps}$
morphism
$\operatorname{fps}$
morphism
![]() $f:Y\rightarrow X$
, and
$f:Y\rightarrow X$
, and
![]() $y\in Y$
, the
$y\in Y$
, the
![]() $y$
th component of the trace morphism
$y$
th component of the trace morphism
![]() $F_{\operatorname{cdd}}(Y)=\prod _{y\in Y}F(y)\rightarrow \prod _{x\in X}F(x)=F_{\operatorname{cdd}}(X)$
is given by
$F_{\operatorname{cdd}}(Y)=\prod _{y\in Y}F(y)\rightarrow \prod _{x\in X}F(x)=F_{\operatorname{cdd}}(X)$
is given by
![]() $(\operatorname{length}\,{\mathcal{O}}_{x\times _{X}Y,y})\operatorname{Tr}_{f|_{y/x}}$
.
$(\operatorname{length}\,{\mathcal{O}}_{x\times _{X}Y,y})\operatorname{Tr}_{f|_{y/x}}$
.
Lemma 28. Suppose that
![]() $F$
is a
$F$
is a
![]() $\operatorname{uh}$
-invariant
$\operatorname{uh}$
-invariant
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1), and
$\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1), and
![]() $R$
a finite rank hvr of positive characteristic
$R$
a finite rank hvr of positive characteristic
![]() $p\neq l$
. Then on the category of finite
$p\neq l$
. Then on the category of finite
![]() $R$
-algebras, there is a factorization
$R$
-algebras, there is a factorization
![]() $F\rightarrow F_{l\operatorname{dh}}\stackrel{\unicode[STIX]{x1D704}}{{\hookrightarrow}}F_{\operatorname{cdd}}$
with
$F\rightarrow F_{l\operatorname{dh}}\stackrel{\unicode[STIX]{x1D704}}{{\hookrightarrow}}F_{\operatorname{cdd}}$
with
![]() $\unicode[STIX]{x1D704}$
a monomorphism.
$\unicode[STIX]{x1D704}$
a monomorphism.
Proof. On hvrs, and in particular on fields,
![]() $F\cong F_{l\operatorname{dh}}$
, Proposition 24, so
$F\cong F_{l\operatorname{dh}}$
, Proposition 24, so
![]() $F_{\operatorname{cdd}}\cong (F_{l\operatorname{dh}})_{\operatorname{cdd}}$
. Our injection is
$F_{\operatorname{cdd}}\cong (F_{l\operatorname{dh}})_{\operatorname{cdd}}$
. Our injection is
![]() $\unicode[STIX]{x1D704}:F_{l\operatorname{dh}}\rightarrow (F_{l\operatorname{dh}})_{\operatorname{cdd}}\stackrel{{\sim}}{\leftarrow }F_{\operatorname{cdd}}$
.
$\unicode[STIX]{x1D704}:F_{l\operatorname{dh}}\rightarrow (F_{l\operatorname{dh}})_{\operatorname{cdd}}\stackrel{{\sim}}{\leftarrow }F_{\operatorname{cdd}}$
.
Let
![]() $A$
be a finite
$A$
be a finite
![]() $R$
-algebra. Spec of the morphism
$R$
-algebra. Spec of the morphism
![]() $A\rightarrow \prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}(A/\mathfrak{p})^{\smallsmile }$
is a
$A\rightarrow \prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}(A/\mathfrak{p})^{\smallsmile }$
is a
![]() $\operatorname{cdh}$
-covering. Since
$\operatorname{cdh}$
-covering. Since
![]() $F_{l\operatorname{dh}}$
is
$F_{l\operatorname{dh}}$
is
![]() $\operatorname{uh}$
-invariant, Corollary 11, each of the morphisms
$\operatorname{uh}$
-invariant, Corollary 11, each of the morphisms
![]() $F_{l\operatorname{dh}}((A/\mathfrak{p})^{\smallsmile })\rightarrow F_{l\operatorname{dh}}((A/\mathfrak{p})^{{\sim}})$
is an isomorphism. But
$F_{l\operatorname{dh}}((A/\mathfrak{p})^{\smallsmile })\rightarrow F_{l\operatorname{dh}}((A/\mathfrak{p})^{{\sim}})$
is an isomorphism. But
![]() $F\cong F_{l\operatorname{dh}}$
on the hvrs
$F\cong F_{l\operatorname{dh}}$
on the hvrs
![]() $(A/\mathfrak{p})^{{\sim}}$
and
$(A/\mathfrak{p})^{{\sim}}$
and
![]() $k(\mathfrak{p})$
, Proposition 29, and
$k(\mathfrak{p})$
, Proposition 29, and
![]() $F$
satisfies (G1), so each
$F$
satisfies (G1), so each
![]() $F_{l\operatorname{dh}}((A/\mathfrak{p})^{{\sim}})\rightarrow F_{l\operatorname{dh}}(k(\mathfrak{p}))$
is injective. Hence,
$F_{l\operatorname{dh}}((A/\mathfrak{p})^{{\sim}})\rightarrow F_{l\operatorname{dh}}(k(\mathfrak{p}))$
is injective. Hence,
![]() $F_{l\operatorname{dh}}(A)\rightarrow \prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}F_{l\operatorname{dh}}(k(\mathfrak{p}))=(F_{l\operatorname{dh}})_{\operatorname{cdd}}(A)\cong F_{\operatorname{cdd}}(A)$
is injective.◻
$F_{l\operatorname{dh}}(A)\rightarrow \prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}F_{l\operatorname{dh}}(k(\mathfrak{p}))=(F_{l\operatorname{dh}})_{\operatorname{cdd}}(A)\cong F_{\operatorname{cdd}}(A)$
is injective.◻
Proposition 29. Suppose that
![]() $F$
is a
$F$
is a
![]() $\operatorname{uh}$
-invariant
$\operatorname{uh}$
-invariant
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1), and
$\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying (G1), and
![]() $R$
is a finite rank hvr of positive characteristic
$R$
is a finite rank hvr of positive characteristic
![]() $p\neq l$
. Then on the category of finite
$p\neq l$
. Then on the category of finite
![]() $R$
-algebras, the trace morphisms on
$R$
-algebras, the trace morphisms on
![]() $F_{\operatorname{cdd}}$
descend to the subpresheaf
$F_{\operatorname{cdd}}$
descend to the subpresheaf
![]() $F_{l\operatorname{dh}}$
. In particular,
$F_{l\operatorname{dh}}$
. In particular,
![]() $F_{l\operatorname{dh}}$
has a structure of traces on the category of finite
$F_{l\operatorname{dh}}$
has a structure of traces on the category of finite
![]() $R$
-algebras.
$R$
-algebras.
Proof. Explicitly, we want to show that for every
![]() $\operatorname{fps}$
-morphism of
$\operatorname{fps}$
-morphism of
![]() $R$
-algebras
$R$
-algebras
![]() $\unicode[STIX]{x1D719}:A\rightarrow B$
, the trace morphism
$\unicode[STIX]{x1D719}:A\rightarrow B$
, the trace morphism
![]() $\operatorname{Tr}_{\unicode[STIX]{x1D719}}:F_{\operatorname{cdd}}(B)\rightarrow F_{\operatorname{cdd}}(A)$
sends the image of
$\operatorname{Tr}_{\unicode[STIX]{x1D719}}:F_{\operatorname{cdd}}(B)\rightarrow F_{\operatorname{cdd}}(A)$
sends the image of
![]() $F_{l\operatorname{dh}}(B){\hookrightarrow}F_{\operatorname{cdd}}(B)$
inside the image of
$F_{l\operatorname{dh}}(B){\hookrightarrow}F_{\operatorname{cdd}}(B)$
inside the image of
![]() $F_{l\operatorname{dh}}(A){\hookrightarrow}F_{\operatorname{cdd}}(A)$
. First note that if
$F_{l\operatorname{dh}}(A){\hookrightarrow}F_{\operatorname{cdd}}(A)$
. First note that if
![]() $A\rightarrow A^{\prime }$
is a morphism whose
$A\rightarrow A^{\prime }$
is a morphism whose
![]() $\operatorname{Spec}$
is a completely decomposed proper (
$\operatorname{Spec}$
is a completely decomposed proper (
![]() $=$
finite) morphism, then a diagram chase using the short exact sequences, Remark 25, associated to
$=$
finite) morphism, then a diagram chase using the short exact sequences, Remark 25, associated to
![]() $A\rightarrow A^{\prime }\rightrightarrows A^{\prime }\otimes _{A}A^{\prime }$
by
$A\rightarrow A^{\prime }\rightrightarrows A^{\prime }\otimes _{A}A^{\prime }$
by
![]() $F_{l\operatorname{dh}}{\hookrightarrow}F_{\operatorname{cdd}}$
shows that
$F_{l\operatorname{dh}}{\hookrightarrow}F_{\operatorname{cdd}}$
shows that
![]() $F_{l\operatorname{dh}}(A)=F_{l\operatorname{dh}}(A^{\prime })\cap F_{\operatorname{cdd}}(A)$
. So replacing
$F_{l\operatorname{dh}}(A)=F_{l\operatorname{dh}}(A^{\prime })\cap F_{\operatorname{cdd}}(A)$
. So replacing
![]() $A$
with
$A$
with
![]() $A^{\prime }=\prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}(A/\mathfrak{p})^{\smallsmile }$
and using (Add) and (CdB), we can assume that
$A^{\prime }=\prod _{\substack{ \mathfrak{p}\subset A \\ \mathfrak{p}~\text{prime}}}(A/\mathfrak{p})^{\smallsmile }$
and using (Add) and (CdB), we can assume that
![]() $A$
is a pseudo-hvr. Now, using the morphism
$A$
is a pseudo-hvr. Now, using the morphism
![]() $B\rightarrow \prod _{\substack{ \mathfrak{q}\subset B \\ \mathfrak{q}~\text{prime}}}(B/\mathfrak{q})^{\smallsmile }$
and the property (Tr) stated in Proposition 26, we can assume that
$B\rightarrow \prod _{\substack{ \mathfrak{q}\subset B \\ \mathfrak{q}~\text{prime}}}(B/\mathfrak{q})^{\smallsmile }$
and the property (Tr) stated in Proposition 26, we can assume that
![]() $B$
is also a pseudo-hvr. So now
$B$
is also a pseudo-hvr. So now
![]() $A\rightarrow B$
is a
$A\rightarrow B$
is a
![]() $\operatorname{fps}$
-morphism between pseudo-hvrs. But then
$\operatorname{fps}$
-morphism between pseudo-hvrs. But then
![]() $F(A)\stackrel{{\sim}}{\rightarrow }F_{l\operatorname{dh}}(A)$
,
$F(A)\stackrel{{\sim}}{\rightarrow }F_{l\operatorname{dh}}(A)$
,
![]() $F(B)\stackrel{{\sim}}{\rightarrow }F_{l\operatorname{dh}}(B)$
are isomorphisms, Proposition 24. So the result follows from the fact that
$F(B)\stackrel{{\sim}}{\rightarrow }F_{l\operatorname{dh}}(B)$
are isomorphisms, Proposition 24. So the result follows from the fact that
![]() $F\rightarrow F_{\operatorname{cdd}}$
is a morphism of presheaves with traces, Proposition 26.◻
$F\rightarrow F_{\operatorname{cdd}}$
is a morphism of presheaves with traces, Proposition 26.◻
8 Comparison of
 $\operatorname{cdh}$
- and
$\operatorname{cdh}$
- and
 $l\operatorname{dh}$
-descent
$l\operatorname{dh}$
-descent
Theorem 30. Suppose
![]() $S$
is a finite dimensional Noetherian separated scheme of positive characteristic
$S$
is a finite dimensional Noetherian separated scheme of positive characteristic
![]() $p\neq l$
and
$p\neq l$
and
![]() $F$
is a
$F$
is a
![]() $\operatorname{uh}$
-invariant
$\operatorname{uh}$
-invariant
![]() $\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying both conditions:
$\mathbb{Z}_{(l)}$
-linear presheaf with traces satisfying both conditions:
- (G1)
 $F(R)\rightarrow F(\operatorname{Frac}(R))$
is injective for every finite rank hvr
$F(R)\rightarrow F(\operatorname{Frac}(R))$
is injective for every finite rank hvr
 $R$
.
$R$
.- (G2)
 $F(R)\rightarrow F(R/\mathfrak{p})$
is surjective for every finite rank hvr
$F(R)\rightarrow F(R/\mathfrak{p})$
is surjective for every finite rank hvr
 $R$
and prime
$R$
and prime
 $\mathfrak{p}$
of codimension one.
$\mathfrak{p}$
of codimension one.
Then the canonical comparison morphism is an isomorphism:
Proof. By the change of topology spectral sequence
it suffices to show that
![]() $F_{\operatorname{cdh}}=F_{l\operatorname{dh}}$
, and
$F_{\operatorname{cdh}}=F_{l\operatorname{dh}}$
, and
![]() $(\text{}\underline{H}_{l\operatorname{dh}}^{j}F)_{\operatorname{cdh}}=0$
for
$(\text{}\underline{H}_{l\operatorname{dh}}^{j}F)_{\operatorname{cdh}}=0$
for
![]() $j>0$
. Since finite rank hvrs form a conservative family of fiber functors for the
$j>0$
. Since finite rank hvrs form a conservative family of fiber functors for the
![]() $\operatorname{cdh}$
-site
$\operatorname{cdh}$
-site
![]() $\mathsf{Sch}_{S}$
, Corollary A.3, and cohomology commutes with filtered limits of schemes with affine transition morphisms, Proposition B.5, it suffices to show that for every finite rank hvr
$\mathsf{Sch}_{S}$
, Corollary A.3, and cohomology commutes with filtered limits of schemes with affine transition morphisms, Proposition B.5, it suffices to show that for every finite rank hvr
![]() $R$
we have
$R$
we have
![]() $F(R)=F_{l\operatorname{dh}}(R)$
, and
$F(R)=F_{l\operatorname{dh}}(R)$
, and
![]() $H_{l\operatorname{dh}}^{j}(R,F_{l\operatorname{dh}})=0$
for
$H_{l\operatorname{dh}}^{j}(R,F_{l\operatorname{dh}})=0$
for
![]() $j>0$
.
$j>0$
.
It was already shown in Proposition 24 that we have
![]() $F(R)=F_{l\operatorname{dh}}(R)$
. We now show that for any finite
$F(R)=F_{l\operatorname{dh}}(R)$
. We now show that for any finite
![]() $R$
-algebra
$R$
-algebra
![]() $A$
, we have
$A$
, we have
for
![]() $j>0$
. We work by induction on
$j>0$
. We work by induction on
![]() $(\dim \operatorname{Spec}(A),j)$
where
$(\dim \operatorname{Spec}(A),j)$
where
![]() $\mathbb{N}\times \mathbb{N}_{{>}0}$
has the lexicographical ordering. Explicitly, we suppose that (1) is true for
$\mathbb{N}\times \mathbb{N}_{{>}0}$
has the lexicographical ordering. Explicitly, we suppose that (1) is true for
![]() $\dim \operatorname{Spec}(A)<\dim \operatorname{Spec}(R)$
, and all
$\dim \operatorname{Spec}(A)<\dim \operatorname{Spec}(R)$
, and all
![]() $0<j$
and suppose also that (1) is true when
$0<j$
and suppose also that (1) is true when
![]() $\dim \operatorname{Spec}(A)=\dim \operatorname{Spec}(R)$
and
$\dim \operatorname{Spec}(A)=\dim \operatorname{Spec}(R)$
and
![]() $0<j<J$
. We will show that it is true for
$0<j<J$
. We will show that it is true for
![]() $\dim \operatorname{Spec}(A)=\dim \operatorname{Spec}(R)$
and
$\dim \operatorname{Spec}(A)=\dim \operatorname{Spec}(R)$
and
![]() $j=J$
.
$j=J$
.
Here is a plan of what we will prove, where
![]() $A^{\prime }=A^{\operatorname{pic}}$
is a pseudo-integral closure of
$A^{\prime }=A^{\operatorname{pic}}$
is a pseudo-integral closure of
![]() $A^{\operatorname{red}}$
in
$A^{\operatorname{red}}$
in
![]() $(Q(R)\otimes _{R}A)^{\operatorname{red}}$
, and
$(Q(R)\otimes _{R}A)^{\operatorname{red}}$
, and
![]() $R^{\prime }=\widetilde{A^{\prime }}$
:
$R^{\prime }=\widetilde{A^{\prime }}$
:

Step
![]() $\unicode[STIX]{x1D6FC}$
. Let
$\unicode[STIX]{x1D6FC}$
. Let
![]() $A^{\prime }=A^{\operatorname{pic}}$
be a pseudo-integral closure of
$A^{\prime }=A^{\operatorname{pic}}$
be a pseudo-integral closure of
![]() $A^{\operatorname{red}}$
inside
$A^{\operatorname{red}}$
inside
![]() $(Q(R)\otimes _{R}A)^{\operatorname{red}}$
, let
$(Q(R)\otimes _{R}A)^{\operatorname{red}}$
, let
![]() $\mathfrak{p}\subset R$
be the prime of height one (if
$\mathfrak{p}\subset R$
be the prime of height one (if
![]() $\dim \operatorname{Spec}(R)=0$
set
$\dim \operatorname{Spec}(R)=0$
set
![]() $\mathfrak{p}$
to be the unit ideal
$\mathfrak{p}$
to be the unit ideal
![]() $\mathfrak{p}=R$
), and consider the blowup sequence, Proposition B.5(5),
$\mathfrak{p}=R$
), and consider the blowup sequence, Proposition B.5(5),
 $$\begin{eqnarray}\displaystyle \cdots & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j-1}(A^{\prime }/\mathfrak{p},F_{l\operatorname{dh}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j}(A,F_{l\operatorname{dh}})\rightarrow H_{l\operatorname{dh}}^{j}(A^{\prime },F_{l\operatorname{dh}})\oplus H_{l\operatorname{dh}}^{j}(A/\mathfrak{p},F_{l\operatorname{dh}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j}(A^{\prime }/\mathfrak{p},F_{l\operatorname{dh}})\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j-1}(A^{\prime }/\mathfrak{p},F_{l\operatorname{dh}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j}(A,F_{l\operatorname{dh}})\rightarrow H_{l\operatorname{dh}}^{j}(A^{\prime },F_{l\operatorname{dh}})\oplus H_{l\operatorname{dh}}^{j}(A/\mathfrak{p},F_{l\operatorname{dh}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle H_{l\operatorname{dh}}^{j}(A^{\prime }/\mathfrak{p},F_{l\operatorname{dh}})\rightarrow \cdots\end{eqnarray}$$
By induction on
![]() $\dim \operatorname{Spec}(A)$
, (1) is true for
$\dim \operatorname{Spec}(A)$
, (1) is true for
![]() $A/\mathfrak{p}$
and
$A/\mathfrak{p}$
and
![]() $A^{\prime }/\mathfrak{p}$
, so we obtain an isomorphism
$A^{\prime }/\mathfrak{p}$
, so we obtain an isomorphism
Here, (G2) and
![]() $\operatorname{uh}$
-invariance of
$\operatorname{uh}$
-invariance of
![]() $F_{l\operatorname{dh}}$
, Corollary 11, is used in the case
$F_{l\operatorname{dh}}$
, Corollary 11, is used in the case
![]() $J=1$
to obtain surjectivity of the morphism
$J=1$
to obtain surjectivity of the morphism
![]() $F_{l\operatorname{dh}}(A^{\prime })\rightarrow F_{l\operatorname{dh}}(A^{\prime }/\mathfrak{p})$
.
$F_{l\operatorname{dh}}(A^{\prime })\rightarrow F_{l\operatorname{dh}}(A^{\prime }/\mathfrak{p})$
.
Step
![]() $\unicode[STIX]{x1D6FD}$
. Note
$\unicode[STIX]{x1D6FD}$
. Note
![]() $\operatorname{Spec}$
of
$\operatorname{Spec}$
of
![]() $A^{\prime }\rightarrow R^{\prime }:=\widetilde{A^{\prime }}$
is a
$A^{\prime }\rightarrow R^{\prime }:=\widetilde{A^{\prime }}$
is a
![]() $\operatorname{uh}$
. Since
$\operatorname{uh}$
. Since
![]() $H_{l\operatorname{dh}}^{J}(-,F_{l\operatorname{dh}})$
is
$H_{l\operatorname{dh}}^{J}(-,F_{l\operatorname{dh}})$
is
![]() $\operatorname{uh}$
-invariant, Corollary 11, we are reduced to showing that
$\operatorname{uh}$
-invariant, Corollary 11, we are reduced to showing that
![]() $H_{l\operatorname{dh}}^{J}(R^{\prime },F_{l\operatorname{dh}})$
vanishes.
$H_{l\operatorname{dh}}^{J}(R^{\prime },F_{l\operatorname{dh}})$
vanishes.
Step
![]() $\unicode[STIX]{x1D6FE}$
. Consider the Čech spectral sequence
$\unicode[STIX]{x1D6FE}$
. Consider the Čech spectral sequence
Note that the
![]() $i=0,j>0$
part vanishes automatically, since
$i=0,j>0$
part vanishes automatically, since
![]() $\check{H}_{\unicode[STIX]{x1D70F}}^{0}(-,\text{}\underline{H}_{\unicode[STIX]{x1D70F}}^{j}F)=0$
vanishes for any topology
$\check{H}_{\unicode[STIX]{x1D70F}}^{0}(-,\text{}\underline{H}_{\unicode[STIX]{x1D70F}}^{j}F)=0$
vanishes for any topology
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $j>0$
. In particular,
$j>0$
. In particular,
Since every
![]() $l\operatorname{dh}$
-covering of
$l\operatorname{dh}$
-covering of
![]() $R^{\prime }$
is refinable by a finite one, Lemma 22, and
$R^{\prime }$
is refinable by a finite one, Lemma 22, and
![]() $\text{}\underline{H}_{l\operatorname{dh}}^{j}F(-)=H_{l\operatorname{dh}}^{j}(-,F_{l\operatorname{dh}})$
vanishes on finite
$\text{}\underline{H}_{l\operatorname{dh}}^{j}F(-)=H_{l\operatorname{dh}}^{j}(-,F_{l\operatorname{dh}})$
vanishes on finite
![]() $R^{\prime }$
-algebras for
$R^{\prime }$
-algebras for
![]() $0<j<J$
by induction, it follows that
$0<j<J$
by induction, it follows that
The vanishing so far, (5) and (6), with the spectral sequence (4) shows that
Step
![]() $\unicode[STIX]{x1D6FF}$
. Since
$\unicode[STIX]{x1D6FF}$
. Since
![]() $R^{\prime }$
is a product of hvrs, every
$R^{\prime }$
is a product of hvrs, every
![]() $l\operatorname{dh}$
-covering is refinable by an
$l\operatorname{dh}$
-covering is refinable by an
![]() ${\operatorname{fps}l^{\prime }}^{\prime }$
-covering, Proposition B.5(4). So it suffices to show that the isomorphic groups
${\operatorname{fps}l^{\prime }}^{\prime }$
-covering, Proposition B.5(4). So it suffices to show that the isomorphic groups
are zero.
Step
![]() $\unicode[STIX]{x1D716}$
. Since
$\unicode[STIX]{x1D716}$
. Since
![]() $F_{l\operatorname{dh}}$
has a structure of traces, Proposition 29, this vanishing follows directly from
$F_{l\operatorname{dh}}$
has a structure of traces, Proposition 29, this vanishing follows directly from
![]() $\mathbb{Z}_{(l)}$
-linearity and the structure of traces, Lemma 15. ◻
$\mathbb{Z}_{(l)}$
-linearity and the structure of traces, Lemma 15. ◻
Acknowledgments
The idea for this strategy is from 2013, but it took five years to realize how to get around the non-Nagataness of valuation rings. This proof owes its existence to Veronika Ertl. It was during discussions with her about de Rham–Witt differentials of valuation rings that I had the idea to use pseudo-normalizations. I thank Giuseppe Ancona, Matthew Morrow, and Simon Pepin-Lehalleur for comments that improved the writing style. I also thank an anonymous referee for helping catch a mathematical error in a previous version.
Appendix A. The
 $\operatorname{cdh}$
- and
$\operatorname{cdh}$
- and
 $l\operatorname{dh}$
-topologies
$l\operatorname{dh}$
-topologies
In [Reference Gabber and KellyGK15] it was observed that Hensel valuation rings, or hvrs, form a conservative family of fiber functors for the
![]() $\operatorname{cdh}$
-site of a Noetherian scheme (see Section 4 for some facts about hvrs). Here, we observe that if
$\operatorname{cdh}$
-site of a Noetherian scheme (see Section 4 for some facts about hvrs). Here, we observe that if
![]() $\dim S$
is finite, then in fact, it suffices to consider hvrs of finite rank.
$\dim S$
is finite, then in fact, it suffices to consider hvrs of finite rank.
Definition A.1. Let
![]() $S$
be a separated Noetherian scheme,
$S$
be a separated Noetherian scheme,
![]() $\mathsf{Sch}_{S}$
the category of separated finite type
$\mathsf{Sch}_{S}$
the category of separated finite type
![]() $S$
-schemes, and
$S$
-schemes, and
![]() $l\in \mathbb{Z}$
a prime. We quickly recall the following definitions.
$l\in \mathbb{Z}$
a prime. We quickly recall the following definitions.
(1) A morphism
 $f:Y\rightarrow X$
is completely decomposed if for all
$f:Y\rightarrow X$
is completely decomposed if for all
 $x\in X$
there exists
$x\in X$
there exists
 $y\in Y$
with
$y\in Y$
with
 $f(y)=x$
and
$f(y)=x$
and
 $k(y)=k(x)$
.
$k(y)=k(x)$
.(2) The
 $\operatorname{cdh}$
-topology is generated by families of étale morphisms
$\operatorname{cdh}$
-topology is generated by families of étale morphisms
 $\{Y_{i}\rightarrow X\}_{i\in I}$
such that
$\{Y_{i}\rightarrow X\}_{i\in I}$
such that
 $\amalg Y_{i}\rightarrow X$
is completely decomposed, and families of proper morphisms
$\amalg Y_{i}\rightarrow X$
is completely decomposed, and families of proper morphisms
 $\{Y_{i}\rightarrow X\}_{i\in I}$
such that
$\{Y_{i}\rightarrow X\}_{i\in I}$
such that
 $\amalg Y_{i}\rightarrow X$
is completely decomposed.
$\amalg Y_{i}\rightarrow X$
is completely decomposed.(3) The
 $l\operatorname{dh}$
-topology is generated by the
$l\operatorname{dh}$
-topology is generated by the
 $\operatorname{cdh}$
-topology, and finite flat surjective morphisms of degree prime to
$\operatorname{cdh}$
-topology, and finite flat surjective morphisms of degree prime to
 $l$
.
$l$
.
Lemma A.2. Let
![]() $A$
be a Noetherian ring,
$A$
be a Noetherian ring,
![]() $R$
a hvr, and
$R$
a hvr, and
![]() $A\rightarrow R$
a morphism. Then
$A\rightarrow R$
a morphism. Then
![]() $R$
is a filtered colimit
$R$
is a filtered colimit
![]() $A$
-algebras which are finite rank hvrs.
$A$
-algebras which are finite rank hvrs.
Proof. Note
![]() $A\rightarrow R$
factors through a localization of
$A\rightarrow R$
factors through a localization of
![]() $A$
, and local Noetherian rings have finite Krull dimension, so we can assume
$A$
, and local Noetherian rings have finite Krull dimension, so we can assume
![]() $A$
has finite Krull dimension. Certainly,
$A$
has finite Krull dimension. Certainly,
![]() $R$
is the filtered union of its finitely generated sub-
$R$
is the filtered union of its finitely generated sub-
![]() $A$
-algebras. For each such
$A$
-algebras. For each such
![]() $A$
-algebra
$A$
-algebra
![]() $A\rightarrow A_{\unicode[STIX]{x1D706}}\subseteq R$
, define
$A\rightarrow A_{\unicode[STIX]{x1D706}}\subseteq R$
, define
![]() $R_{\unicode[STIX]{x1D706}}=\operatorname{Frac}(A_{\unicode[STIX]{x1D706}})\cap R\subseteq \operatorname{Frac}(R)$
to be the valuation ring induced on the fraction field of
$R_{\unicode[STIX]{x1D706}}=\operatorname{Frac}(A_{\unicode[STIX]{x1D706}})\cap R\subseteq \operatorname{Frac}(R)$
to be the valuation ring induced on the fraction field of
![]() $A_{\unicode[STIX]{x1D706}}$
by
$A_{\unicode[STIX]{x1D706}}$
by
![]() $R$
. This is finite rank: Certainly,
$R$
. This is finite rank: Certainly,
![]() $R_{\unicode[STIX]{x1D706}}$
is the union of its finitely generated sub-
$R_{\unicode[STIX]{x1D706}}$
is the union of its finitely generated sub-
![]() $A_{\unicode[STIX]{x1D706}}$
-algebras
$A_{\unicode[STIX]{x1D706}}$
-algebras
![]() $A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}\subseteq R_{\unicode[STIX]{x1D706}}$
. By
$A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}\subseteq R_{\unicode[STIX]{x1D706}}$
. By
![]() $A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}\subseteq \operatorname{Frac}(A_{\unicode[STIX]{x1D706}})$
we have
$A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}\subseteq \operatorname{Frac}(A_{\unicode[STIX]{x1D706}})$
we have
![]() $\operatorname{Frac}(A_{\unicode[STIX]{x1D706}})=\operatorname{Frac}(A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}})$
so
$\operatorname{Frac}(A_{\unicode[STIX]{x1D706}})=\operatorname{Frac}(A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}})$
so
![]() $\dim A_{\unicode[STIX]{x1D706}}\geqslant \dim A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
[Reference GrothendieckEGAIV2, Theorem 5.5.8], and thereforeFootnote
6
$\dim A_{\unicode[STIX]{x1D706}}\geqslant \dim A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
[Reference GrothendieckEGAIV2, Theorem 5.5.8], and thereforeFootnote
6
![]() $\dim \operatorname{Spec}(A_{\unicode[STIX]{x1D706}})\geqslant \dim \operatorname{Spec}(R_{\unicode[STIX]{x1D706}})$
.
$\dim \operatorname{Spec}(A_{\unicode[STIX]{x1D706}})\geqslant \dim \operatorname{Spec}(R_{\unicode[STIX]{x1D706}})$
.
Consider the Henselizations
![]() $R_{\unicode[STIX]{x1D706}}^{h}$
of the
$R_{\unicode[STIX]{x1D706}}^{h}$
of the
![]() $R_{\unicode[STIX]{x1D706}}$
. Henselizations of valuation rings are valuation rings of the same rank, [Stacks, Tag 0ASK], so the
$R_{\unicode[STIX]{x1D706}}$
. Henselizations of valuation rings are valuation rings of the same rank, [Stacks, Tag 0ASK], so the
![]() $R_{\unicode[STIX]{x1D706}}^{h}$
are also of finite rank. The inclusion
$R_{\unicode[STIX]{x1D706}}^{h}$
are also of finite rank. The inclusion
![]() $R_{\unicode[STIX]{x1D706}}\subseteq R$
extends uniquely to an inclusionFootnote
7
$R_{\unicode[STIX]{x1D706}}\subseteq R$
extends uniquely to an inclusionFootnote
7
![]() $R_{\unicode[STIX]{x1D706}}^{h}\subseteq R$
as
$R_{\unicode[STIX]{x1D706}}^{h}\subseteq R$
as
![]() $R_{\unicode[STIX]{x1D706}}\subseteq R$
local morphism of local rings (indeed
$R_{\unicode[STIX]{x1D706}}\subseteq R$
local morphism of local rings (indeed
![]() $R_{\unicode[STIX]{x1D706}}^{\ast }=R^{\ast }$
) toward a Hensel local ring. Moreover, any inclusion of finitely generated sub-
$R_{\unicode[STIX]{x1D706}}^{\ast }=R^{\ast }$
) toward a Hensel local ring. Moreover, any inclusion of finitely generated sub-
![]() $A$
-algebras
$A$
-algebras
![]() $A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}^{\prime }}\subseteq R$
induces a unique factorization
$A_{\unicode[STIX]{x1D706}}\subseteq A_{\unicode[STIX]{x1D706}^{\prime }}\subseteq R$
induces a unique factorization
![]() $R_{\unicode[STIX]{x1D706}}^{h}\subseteq R_{\unicode[STIX]{x1D706}^{\prime }}^{h}\subseteq R$
for the same reason. For every
$R_{\unicode[STIX]{x1D706}}^{h}\subseteq R_{\unicode[STIX]{x1D706}^{\prime }}^{h}\subseteq R$
for the same reason. For every
![]() $a\in R$
, there is a finitely generated sub-
$a\in R$
, there is a finitely generated sub-
![]() $A$
-algebra
$A$
-algebra
![]() $A_{\unicode[STIX]{x1D706}}$
with
$A_{\unicode[STIX]{x1D706}}$
with
![]() $a\in A_{\unicode[STIX]{x1D706}}$
. Clearly, this implies
$a\in A_{\unicode[STIX]{x1D706}}$
. Clearly, this implies
![]() $a\in R_{\unicode[STIX]{x1D706}}$
, so
$a\in R_{\unicode[STIX]{x1D706}}$
, so
![]() $a\in R_{\unicode[STIX]{x1D706}}^{h}$
, and it follows that
$a\in R_{\unicode[STIX]{x1D706}}^{h}$
, and it follows that
![]() $R$
is the union of the finite rank hvrs
$R$
is the union of the finite rank hvrs
![]() $R_{\unicode[STIX]{x1D706}}$
, and this is a filtered union because the poset
$R_{\unicode[STIX]{x1D706}}$
, and this is a filtered union because the poset
![]() $\{A_{\unicode[STIX]{x1D706}}\}$
is filtered.◻
$\{A_{\unicode[STIX]{x1D706}}\}$
is filtered.◻
Corollary A.3. Let
![]() $S$
be a Noetherian separated scheme, and
$S$
be a Noetherian separated scheme, and
![]() $\mathsf{Sch}_{S}$
the category of finite type separated
$\mathsf{Sch}_{S}$
the category of finite type separated
![]() $S$
-schemes equipped with the
$S$
-schemes equipped with the
![]() $\operatorname{cdh}$
-topology. For any
$\operatorname{cdh}$
-topology. For any
![]() $S$
-scheme
$S$
-scheme
![]() $P\rightarrow S$
define
$P\rightarrow S$
define
where the colimit is over factorizations with
![]() $X\rightarrow S$
in
$X\rightarrow S$
in
![]() $\mathsf{Sch}_{S}$
. Then the family of functors
$\mathsf{Sch}_{S}$
. Then the family of functors
is a conservative family of fiber functors.
Proof. It was proven in [Reference Gabber and KellyGK15, Theorems 2.3 and 2.6] that the family of all hvrs induces a conservative family of fiber functors. But Lemma A.2 says that any hvr is a filtered colimit of finite rank hvrs. So given a cdh-sheaf
![]() $F$
, if
$F$
, if
![]() $F(R)=0$
for every finite rank hvr, we have
$F(R)=0$
for every finite rank hvr, we have
![]() $F(R)=0$
for all hvrs, and therefore
$F(R)=0$
for all hvrs, and therefore
![]() $F=0$
.◻
$F=0$
.◻
Appendix B. Sites of non-Noetherian schemes
Definition B.1. We write
![]() $\mathsf{SCH}_{S}$
for the category of all
Footnote
8
quasi-compact separated (and therefore quasi-separated)
$\mathsf{SCH}_{S}$
for the category of all
Footnote
8
quasi-compact separated (and therefore quasi-separated)
![]() $S$
-schemes.
$S$
-schemes.
Remark B.2. Since our base scheme
![]() $S$
will always be a Noetherian separated scheme, and in particular quasi-compact quasi-separated,
$S$
will always be a Noetherian separated scheme, and in particular quasi-compact quasi-separated,
![]() $\mathsf{SCH}_{S}$
is nothing more than the category of those
$\mathsf{SCH}_{S}$
is nothing more than the category of those
![]() $S$
-schemes
$S$
-schemes
![]() $T\rightarrow S$
of the form
$T\rightarrow S$
of the form
![]() $T=\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}T_{\unicode[STIX]{x1D706}}$
for some filtered system
$T=\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}T_{\unicode[STIX]{x1D706}}$
for some filtered system
![]() $T_{-}:\unicode[STIX]{x1D6EC}\rightarrow \mathsf{Sch}_{S}$
with affine transition morphisms, [Reference TemkinTem11, Theorem 1.1.2].
$T_{-}:\unicode[STIX]{x1D6EC}\rightarrow \mathsf{Sch}_{S}$
with affine transition morphisms, [Reference TemkinTem11, Theorem 1.1.2].
Remark B.3. Following Suslin and Voevodsky, we use the term covering family in the sense of [SGA4, Exp. II. Definition 1.2]. That is, in addition to satisfying the axioms of a pretopology, any family refinable by a covering family is a covering family.
Proposition B.4. Let
![]() $S$
be a Noetherian separated scheme, let
$S$
be a Noetherian separated scheme, let
![]() $\unicode[STIX]{x1D70F}$
be a topology on
$\unicode[STIX]{x1D70F}$
be a topology on
![]() $\mathsf{Sch}_{S}$
such that every covering family is refinable by one indexed by a finite set, and let
$\mathsf{Sch}_{S}$
such that every covering family is refinable by one indexed by a finite set, and let
![]() $\unicode[STIX]{x1D70F}^{\prime }$
be the coarsest topology on
$\unicode[STIX]{x1D70F}^{\prime }$
be the coarsest topology on
![]() $\mathsf{SCH}_{S}$
making
$\mathsf{SCH}_{S}$
making
![]() $\mathsf{Sch}_{S}\rightarrow \mathsf{SCH}_{S}$
continuous (cf. [SGA4, Exp. III. Proposition 1.6]). Then the covering families for
$\mathsf{Sch}_{S}\rightarrow \mathsf{SCH}_{S}$
continuous (cf. [SGA4, Exp. III. Proposition 1.6]). Then the covering families for
![]() $\unicode[STIX]{x1D70F}^{\prime }$
are those families which are refinable by pullbacks of covering families in
$\unicode[STIX]{x1D70F}^{\prime }$
are those families which are refinable by pullbacks of covering families in
![]() $\mathsf{Sch}_{S}$
.
$\mathsf{Sch}_{S}$
.
Proof. Certainly any
![]() $\unicode[STIX]{x1D70F}$
-covering family in
$\unicode[STIX]{x1D70F}$
-covering family in
![]() $\mathsf{Sch}_{S}$
must be a
$\mathsf{Sch}_{S}$
must be a
![]() $\unicode[STIX]{x1D70F}^{\prime }$
-covering family in
$\unicode[STIX]{x1D70F}^{\prime }$
-covering family in
![]() $\mathsf{SCH}_{S}$
, and therefore the pullback of any
$\mathsf{SCH}_{S}$
, and therefore the pullback of any
![]() $\unicode[STIX]{x1D70F}$
-covering family in
$\unicode[STIX]{x1D70F}$
-covering family in
![]() $\mathsf{Sch}_{S}$
must also be a
$\mathsf{Sch}_{S}$
must also be a
![]() $\unicode[STIX]{x1D70F}^{\prime }$
-covering family in
$\unicode[STIX]{x1D70F}^{\prime }$
-covering family in
![]() $\mathsf{SCH}_{S}$
, so it suffices to show that the collection of such families (i) contains the identity family, (ii) is closed under pullback, and (iii) is closed under “composition” in the sense that if
$\mathsf{SCH}_{S}$
, so it suffices to show that the collection of such families (i) contains the identity family, (ii) is closed under pullback, and (iii) is closed under “composition” in the sense that if
![]() ${\{U_{i}^{\prime }\rightarrow X^{\prime }\}}_{i\in I}$
and
${\{U_{i}^{\prime }\rightarrow X^{\prime }\}}_{i\in I}$
and
![]() ${\{V_{ij}^{\prime }\rightarrow U_{i}^{\prime }\}}_{j\in J_{i}}$
are such families, then so is
${\{V_{ij}^{\prime }\rightarrow U_{i}^{\prime }\}}_{j\in J_{i}}$
are such families, then so is
![]() ${\{V_{ij}^{\prime }\rightarrow X^{\prime }\}}_{i\in I,i\in J_{i}}$
. The first two are clear, so consider the third. By hypothesis, without loss of generality we can assume that
${\{V_{ij}^{\prime }\rightarrow X^{\prime }\}}_{i\in I,i\in J_{i}}$
. The first two are clear, so consider the third. By hypothesis, without loss of generality we can assume that
![]() $I$
is finite. Suppose
$I$
is finite. Suppose
![]() $U_{i}^{\prime }\rightarrow Y_{i}$
, and
$U_{i}^{\prime }\rightarrow Y_{i}$
, and
![]() $X^{\prime }\rightarrow X$
are morphisms with
$X^{\prime }\rightarrow X$
are morphisms with
![]() $Y_{i},X\in \mathsf{Sch}_{S}$
, and
$Y_{i},X\in \mathsf{Sch}_{S}$
, and
![]() $\{V_{ij}\rightarrow Y_{i}\},\{U_{i}\rightarrow X\}$
are
$\{V_{ij}\rightarrow Y_{i}\},\{U_{i}\rightarrow X\}$
are
![]() $\unicode[STIX]{x1D70F}$
-coverings such that
$\unicode[STIX]{x1D70F}$
-coverings such that
![]() $U_{i}^{\prime }=U_{i}\times _{X}X^{\prime }$
and
$U_{i}^{\prime }=U_{i}\times _{X}X^{\prime }$
and
![]() $V_{ij}^{\prime }=V_{ij}\times _{Y_{i}}U_{i}^{\prime }$
.
$V_{ij}^{\prime }=V_{ij}\times _{Y_{i}}U_{i}^{\prime }$
.

Without loss of generality we can assume that
![]() $X^{\prime }$
is the limit
$X^{\prime }$
is the limit
![]() $\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D6EC}}X_{\unicode[STIX]{x1D706}}$
of a filtered system
$\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D6EC}}X_{\unicode[STIX]{x1D706}}$
of a filtered system
![]() $\{X_{\unicode[STIX]{x1D706}}\}$
in
$\{X_{\unicode[STIX]{x1D706}}\}$
in
![]() $\mathsf{Sch}_{S}$
with affine transition morphisms (cf. Remark B.2), and since
$\mathsf{Sch}_{S}$
with affine transition morphisms (cf. Remark B.2), and since
![]() $\hom (\varprojlim X_{\unicode[STIX]{x1D706}},X)=\varinjlim \hom (X_{\unicode[STIX]{x1D706}},X)$
[Reference GrothendieckEGAIV3, Corollary 8.13.2] that
$\hom (\varprojlim X_{\unicode[STIX]{x1D706}},X)=\varinjlim \hom (X_{\unicode[STIX]{x1D706}},X)$
[Reference GrothendieckEGAIV3, Corollary 8.13.2] that
![]() $X=X_{\unicode[STIX]{x1D706}_{0}}$
for some
$X=X_{\unicode[STIX]{x1D706}_{0}}$
for some
![]() $\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
. In particular, now
$\unicode[STIX]{x1D706}_{0}\in \unicode[STIX]{x1D6EC}$
. In particular, now
![]() $U_{i}^{\prime }=\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i})$
. Now since
$U_{i}^{\prime }=\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i})$
. Now since
![]() $\hom (\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i}),Y_{i})=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}\hom (X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i},Y_{i})$
[Reference GrothendieckEGAIV3, Corollary 8.13.2], for each
$\hom (\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i}),Y_{i})=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}}\hom (X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i},Y_{i})$
[Reference GrothendieckEGAIV3, Corollary 8.13.2], for each
![]() $i$
we can assume that
$i$
we can assume that
![]() $Y_{i}=X_{\unicode[STIX]{x1D706}_{i}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i}$
for some
$Y_{i}=X_{\unicode[STIX]{x1D706}_{i}}\times _{X_{\unicode[STIX]{x1D706}_{0}}}U_{i}$
for some
![]() $\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D706}_{0}$
. Choosing a
$\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D706}_{0}$
. Choosing a
![]() $\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D706}_{i}$
small enough (this is where we use finiteness of
$\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D706}_{i}$
small enough (this is where we use finiteness of
![]() $I$
) and pulling back everything to
$I$
) and pulling back everything to
![]() $X_{\unicode[STIX]{x1D707}}$
, we can assume that
$X_{\unicode[STIX]{x1D707}}$
, we can assume that
![]() $Y_{i}=U_{i}$
. In this case,
$Y_{i}=U_{i}$
. In this case,
![]() $\{V_{ij}^{\prime }\rightarrow U_{i}^{\prime }\rightarrow X^{\prime }\}$
is the pullback of the
$\{V_{ij}^{\prime }\rightarrow U_{i}^{\prime }\rightarrow X^{\prime }\}$
is the pullback of the
![]() $\unicode[STIX]{x1D70F}$
-covering family
$\unicode[STIX]{x1D70F}$
-covering family
![]() $\{V_{ij}\rightarrow U_{i}\rightarrow X_{\unicode[STIX]{x1D707}}\}$
in
$\{V_{ij}\rightarrow U_{i}\rightarrow X_{\unicode[STIX]{x1D707}}\}$
in
![]() $\mathsf{Sch}_{S}$
.◻
$\mathsf{Sch}_{S}$
.◻
In light of Proposition B.4, the
![]() $\unicode[STIX]{x1D70F}^{\prime }$
-covers in
$\unicode[STIX]{x1D70F}^{\prime }$
-covers in
![]() $\mathsf{Sch}_{S}$
are refinable by the
$\mathsf{Sch}_{S}$
are refinable by the
![]() $\unicode[STIX]{x1D70F}$
-covers, so for such topologies (e.g.,
$\unicode[STIX]{x1D70F}$
-covers, so for such topologies (e.g.,
![]() $\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
) we use the same symbol to denote the induced topology on
$\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
) we use the same symbol to denote the induced topology on
![]() $\mathsf{SCH}_{S}$
. Another consequence of this observation is that the adjunction
$\mathsf{SCH}_{S}$
. Another consequence of this observation is that the adjunction
induced by the continuous functor
![]() $\mathsf{Sch}_{S}\rightarrow \mathsf{SCH}_{S}$
satisfies
$\mathsf{Sch}_{S}\rightarrow \mathsf{SCH}_{S}$
satisfies
![]() $\unicode[STIX]{x1D704}_{s}\unicode[STIX]{x1D704}^{s}=\operatorname{id}$
. See [SGA4, Exposé 3] for some material about this basic adjunction. We will write
$\unicode[STIX]{x1D704}_{s}\unicode[STIX]{x1D704}^{s}=\operatorname{id}$
. See [SGA4, Exposé 3] for some material about this basic adjunction. We will write
for the presheaf adjunction.
Proposition B.5. Let
![]() $S$
be a Noetherian separated scheme, and
$S$
be a Noetherian separated scheme, and
![]() $T\rightarrow S$
in
$T\rightarrow S$
in
![]() $\mathsf{SCH}_{S}$
. Write
$\mathsf{SCH}_{S}$
. Write
![]() $T$
as the limit
$T$
as the limit
of some filtered system
![]() $\{T_{\unicode[STIX]{x1D706}}\}$
in
$\{T_{\unicode[STIX]{x1D706}}\}$
in
![]() $\mathsf{Sch}_{S}$
with affine transition morphisms (cf. Remark B.2). Let
$\mathsf{Sch}_{S}$
with affine transition morphisms (cf. Remark B.2). Let
![]() $\unicode[STIX]{x1D70F}$
be both a topology on
$\unicode[STIX]{x1D70F}$
be both a topology on
![]() $\mathsf{Sch}_{S}$
such that every covering family is refinable by one indexed by a finite set, and also the induced topology on
$\mathsf{Sch}_{S}$
such that every covering family is refinable by one indexed by a finite set, and also the induced topology on
![]() $\mathsf{SCH}_{S}$
, for example,
$\mathsf{SCH}_{S}$
, for example,
![]() $\unicode[STIX]{x1D70F}=\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
.
$\unicode[STIX]{x1D70F}=\operatorname{cdh},l\operatorname{dh},\operatorname{fps}l^{\prime }$
.
(1)
 $\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\check{H}_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)\stackrel{{\sim}}{\rightarrow }\check{H}_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{\ast }F)$
for any presheaf
$\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\check{H}_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)\stackrel{{\sim}}{\rightarrow }\check{H}_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{\ast }F)$
for any presheaf
 $F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
.
$F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
.(2)
 $H_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{s}F)=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}H_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)$
for any sheaf
$H_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{s}F)=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}H_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)$
for any sheaf
 $F\in \mathsf{Shv}_{\unicode[STIX]{x1D70F}}(\mathsf{Sch}_{S})$
.
$F\in \mathsf{Shv}_{\unicode[STIX]{x1D70F}}(\mathsf{Sch}_{S})$
.(3) Every
 $l\operatorname{dh}$
-cover of
$l\operatorname{dh}$
-cover of
 $T$
is refinable by the composition of a
$T$
is refinable by the composition of a
 $\operatorname{cdh}$
-cover
$\operatorname{cdh}$
-cover
 $\{V_{i}\rightarrow T\}_{i=1}^{n}$
and
$\{V_{i}\rightarrow T\}_{i=1}^{n}$
and
 $\operatorname{fps}l^{\prime }$
morphisms
$\operatorname{fps}l^{\prime }$
morphisms
 $W_{i}\rightarrow V_{i}$
.
$W_{i}\rightarrow V_{i}$
.(4) Every
 $l\operatorname{dh}$
-cover of the spectrum of an hvr is refinable by an
$l\operatorname{dh}$
-cover of the spectrum of an hvr is refinable by an
 $\operatorname{fps}l^{\prime }$
-morphism.
$\operatorname{fps}l^{\prime }$
-morphism.(5) If
 $Z\rightarrow T$
a closed immersion, and
$Z\rightarrow T$
a closed immersion, and
 $Y\rightarrow T$
a proper morphism, such that
$Y\rightarrow T$
a proper morphism, such that
 $Y\setminus Z\times _{T}Y\rightarrow T\setminus Z$
is an isomorphism, then becomes a short exact sequence after
$Y\setminus Z\times _{T}Y\rightarrow T\setminus Z$
is an isomorphism, then becomes a short exact sequence after $$\begin{eqnarray}0\rightarrow \mathbb{Z}(Z\times _{T}Y)\rightarrow \mathbb{Z}(Z)\oplus \mathbb{Z}(Y)\rightarrow \mathbb{Z}(T)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathbb{Z}(Z\times _{T}Y)\rightarrow \mathbb{Z}(Z)\oplus \mathbb{Z}(Y)\rightarrow \mathbb{Z}(T)\rightarrow 0\end{eqnarray}$$
 $\operatorname{cdh}$
-sheafification, where
$\operatorname{cdh}$
-sheafification, where
 $\mathbb{Z}(W):=\mathbb{Z}\hom _{\mathsf{SCH}_{S}}(-,W)$
.
$\mathbb{Z}(W):=\mathbb{Z}\hom _{\mathsf{SCH}_{S}}(-,W)$
.(6) If
 $F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
has a structure of traces, then
$F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
has a structure of traces, then
 $\unicode[STIX]{x1D704}^{\ast }F\in \mathsf{PreShv}(\mathsf{SCH}_{S})$
inherits a canonical structure of traces extending that of
$\unicode[STIX]{x1D704}^{\ast }F\in \mathsf{PreShv}(\mathsf{SCH}_{S})$
inherits a canonical structure of traces extending that of
 $F$
.
$F$
.(7) If
 $F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
is
$F\in \mathsf{PreShv}(\mathsf{Sch}_{S})$
is
 $\operatorname{uh}$
-invariant, then
$\operatorname{uh}$
-invariant, then
 $\unicode[STIX]{x1D704}^{\ast }F\in \mathsf{PreShv}(\mathsf{SCH}_{S})$
is invariant for finitely presented
$\unicode[STIX]{x1D704}^{\ast }F\in \mathsf{PreShv}(\mathsf{SCH}_{S})$
is invariant for finitely presented
 $\operatorname{uh}$
-morphisms, and
$\operatorname{uh}$
-morphisms, and
 $\operatorname{uh}$
-morphisms between affine schemes with finitely many points.
$\operatorname{uh}$
-morphisms between affine schemes with finitely many points.
Remark B.6. In part (7) we can actually prove that
![]() $\unicode[STIX]{x1D704}^{\ast }F$
is invariant for all
$\unicode[STIX]{x1D704}^{\ast }F$
is invariant for all
![]() $\operatorname{uh}$
-morphisms, assuming only that
$\operatorname{uh}$
-morphisms, assuming only that
![]() $S$
is quasi-compact and quasi-separated, but as we do not need this stronger more general statement in this present work, we do not include its proof. In fact, David Rydh explained to us that the proof below works more or less unchanged, with quasi-compactness of the constructible topology in place of the hypothesis that the schemes have finitely many points.
$S$
is quasi-compact and quasi-separated, but as we do not need this stronger more general statement in this present work, we do not include its proof. In fact, David Rydh explained to us that the proof below works more or less unchanged, with quasi-compactness of the constructible topology in place of the hypothesis that the schemes have finitely many points.
Proof.
(1) Both surjectivity and injectivity follows directly from Proposition B.4 together with [Reference GrothendieckEGAIV3, Theorem 8.8.2] saying that morphisms over
 $T$
lift through the filtered system
$T$
lift through the filtered system
 $\{T_{\unicode[STIX]{x1D706}}\}$
.
$\{T_{\unicode[STIX]{x1D706}}\}$
.(2) As
 $i^{s}$
is exact, the functor
$i^{s}$
is exact, the functor
 $i_{s}$
preserves injective resolutions.Footnote
9
Then any injective resolution of
$i_{s}$
preserves injective resolutions.Footnote
9
Then any injective resolution of
 $\unicode[STIX]{x1D704}^{s}F\rightarrow {\mathcal{I}}^{\bullet }$
restricts to an injective resolution
$\unicode[STIX]{x1D704}^{s}F\rightarrow {\mathcal{I}}^{\bullet }$
restricts to an injective resolution
 $F=\unicode[STIX]{x1D704}_{s}\unicode[STIX]{x1D704}^{s}F\rightarrow \unicode[STIX]{x1D704}_{s}{\mathcal{I}}^{\bullet }$
, and we have
$F=\unicode[STIX]{x1D704}_{s}\unicode[STIX]{x1D704}^{s}F\rightarrow \unicode[STIX]{x1D704}_{s}{\mathcal{I}}^{\bullet }$
, and we have
 $H_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{s}F)=(H^{n}{\mathcal{I}}^{\bullet })(T)=(H^{n}{\mathcal{I}}^{\bullet })(\varprojlim T_{\unicode[STIX]{x1D706}})\stackrel{(\ast )}{=}\varinjlim (H^{n}{\mathcal{I}}^{\bullet })(T_{\unicode[STIX]{x1D706}})=\varinjlim (H^{n}\unicode[STIX]{x1D704}_{s}{\mathcal{I}}^{\bullet })(T_{\unicode[STIX]{x1D706}})=\varinjlim H_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)$
. For (*) note for any injective sheaf
$H_{\unicode[STIX]{x1D70F}}^{n}(T,\unicode[STIX]{x1D704}^{s}F)=(H^{n}{\mathcal{I}}^{\bullet })(T)=(H^{n}{\mathcal{I}}^{\bullet })(\varprojlim T_{\unicode[STIX]{x1D706}})\stackrel{(\ast )}{=}\varinjlim (H^{n}{\mathcal{I}}^{\bullet })(T_{\unicode[STIX]{x1D706}})=\varinjlim (H^{n}\unicode[STIX]{x1D704}_{s}{\mathcal{I}}^{\bullet })(T_{\unicode[STIX]{x1D706}})=\varinjlim H_{\unicode[STIX]{x1D70F}}^{n}(T_{\unicode[STIX]{x1D706}},F)$
. For (*) note for any injective sheaf
 $I$
,
$I$
,
 $\hom (-,I)$
is exact by definition, and Yoneda, and sheafification are both left exact.
$\hom (-,I)$
is exact by definition, and Yoneda, and sheafification are both left exact.(3) By Proposition B.4, this follows from the case where
 $T\in \mathsf{Sch}_{S}$
which is well-known, [Reference KellyKel17, Proposition 2.1.12(iii)]. This latter is proved using Raynaud–Gruson flatification, see also the proof of Lemma 8.
$T\in \mathsf{Sch}_{S}$
which is well-known, [Reference KellyKel17, Proposition 2.1.12(iii)]. This latter is proved using Raynaud–Gruson flatification, see also the proof of Lemma 8.(4) By part (3), every
 $l\operatorname{dh}$
-cover is refinable by a
$l\operatorname{dh}$
-cover is refinable by a
 ${\operatorname{fps}l^{\prime }}^{\prime }$
-cover followed by a
${\operatorname{fps}l^{\prime }}^{\prime }$
-cover followed by a
 $\operatorname{cdh}$
-cover. But every
$\operatorname{cdh}$
-cover. But every
 $\operatorname{cdh}$
-cover of a hvr has a section: for completely decomposed proper morphisms this follows from the valuative criterion for properness, and for completely decomposed étale morphisms, this follows from Hensel’s Lemma.
$\operatorname{cdh}$
-cover of a hvr has a section: for completely decomposed proper morphisms this follows from the valuative criterion for properness, and for completely decomposed étale morphisms, this follows from Hensel’s Lemma.(5) To check exactness, it suffices to check exactness after evaluating the sequence of presheaves on an hvr. But in this case one readily checks exactness using the valuative criterion for properness.
(6) Given a finite flat surjective morphism
 $f:Y\rightarrow X$
in
$f:Y\rightarrow X$
in
 $\mathsf{SCH}_{S}$
, there is a filtered system
$\mathsf{SCH}_{S}$
, there is a filtered system
 $(X_{\unicode[STIX]{x1D706}})$
in
$(X_{\unicode[STIX]{x1D706}})$
in
 $\mathsf{Sch}_{S}$
with affine transition morphisms, Remark B.2, such that
$\mathsf{Sch}_{S}$
with affine transition morphisms, Remark B.2, such that
 $X=\varprojlim X_{\unicode[STIX]{x1D706}}$
, there is some
$X=\varprojlim X_{\unicode[STIX]{x1D706}}$
, there is some
 $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
 $f_{\unicode[STIX]{x1D6FC}}:Y_{\unicode[STIX]{x1D6FC}}\rightarrow X_{\unicode[STIX]{x1D6FC}}$
in
$f_{\unicode[STIX]{x1D6FC}}:Y_{\unicode[STIX]{x1D6FC}}\rightarrow X_{\unicode[STIX]{x1D6FC}}$
in
 $\mathsf{Sch}_{S}$
such that
$\mathsf{Sch}_{S}$
such that
 $f=X\times _{X_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}}$
, [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii)]. We can assume
$f=X\times _{X_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}}$
, [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii)]. We can assume
 $f_{\unicode[STIX]{x1D6FC}}$
is surjective and finite, [Reference GrothendieckEGAIV3, Theorem 8.10.5]. By restricting to finitely many affine opens
$f_{\unicode[STIX]{x1D6FC}}$
is surjective and finite, [Reference GrothendieckEGAIV3, Theorem 8.10.5]. By restricting to finitely many affine opens
 $U\subseteq X_{\unicode[STIX]{x1D6FC}}$
, and choosing isomorphism inducing global sections
$U\subseteq X_{\unicode[STIX]{x1D6FC}}$
, and choosing isomorphism inducing global sections
 ${\mathcal{O}}_{X}^{d}\rightarrow f_{\ast }{\mathcal{O}}_{Y}$
, we see that we can also assume
${\mathcal{O}}_{X}^{d}\rightarrow f_{\ast }{\mathcal{O}}_{Y}$
, we see that we can also assume
 $f_{\unicode[STIX]{x1D6FC}}$
is flat. Note that Noetherianness was used here to kill
$f_{\unicode[STIX]{x1D6FC}}$
is flat. Note that Noetherianness was used here to kill
 $\ker ({\mathcal{O}}_{X}^{d}\rightarrow f_{\ast }{\mathcal{O}}_{Y})$
.
$\ker ({\mathcal{O}}_{X}^{d}\rightarrow f_{\ast }{\mathcal{O}}_{Y})$
.Now define trace morphisms on
 $\unicode[STIX]{x1D704}^{\ast }F$
by choosing such presentations and define
$\unicode[STIX]{x1D704}^{\ast }F$
by choosing such presentations and define
 $\operatorname{Tr}_{f}$
to be
$\operatorname{Tr}_{f}$
to be
 $\varinjlim \operatorname{Tr}_{f_{\unicode[STIX]{x1D706}}}$
. Note that this is well defined. Let
$\varinjlim \operatorname{Tr}_{f_{\unicode[STIX]{x1D706}}}$
. Note that this is well defined. Let
 $a\in F(Y)$
be represented by some
$a\in F(Y)$
be represented by some
 $a_{\unicode[STIX]{x1D706}}\in F(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}})$
, and let
$a_{\unicode[STIX]{x1D706}}\in F(X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}})$
, and let
 $(X_{\unicode[STIX]{x1D706}}^{\prime }),f_{\unicode[STIX]{x1D6FC}}^{\prime }:Y_{\unicode[STIX]{x1D6FC}}^{\prime }\rightarrow X_{\unicode[STIX]{x1D6FC}}^{\prime },a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }\in F(X_{\unicode[STIX]{x1D706}}^{\prime }\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime })$
be some other choice of representative. By [Reference GrothendieckEGAIV3, Proposition 8.13.1] the canonical morphism
$(X_{\unicode[STIX]{x1D706}}^{\prime }),f_{\unicode[STIX]{x1D6FC}}^{\prime }:Y_{\unicode[STIX]{x1D6FC}}^{\prime }\rightarrow X_{\unicode[STIX]{x1D6FC}}^{\prime },a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }\in F(X_{\unicode[STIX]{x1D706}}^{\prime }\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime })$
be some other choice of representative. By [Reference GrothendieckEGAIV3, Proposition 8.13.1] the canonical morphism
 $X\rightarrow X_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
factors as some
$X\rightarrow X_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
factors as some
 $X\rightarrow X_{\unicode[STIX]{x1D707}}\rightarrow X_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
. Since
$X\rightarrow X_{\unicode[STIX]{x1D707}}\rightarrow X_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
. Since
 $X\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\cong Y\cong X\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }$
, there exists some possibly smaller
$X\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\cong Y\cong X\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }$
, there exists some possibly smaller
 $\unicode[STIX]{x1D707}$
and an isomorphism
$\unicode[STIX]{x1D707}$
and an isomorphism
 $X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\cong X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }$
compatible with the former [Reference GrothendieckEGAIV3, Theorem 8.8.2(i)]. As
$X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\cong X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }$
compatible with the former [Reference GrothendieckEGAIV3, Theorem 8.8.2(i)]. As
 $a_{\unicode[STIX]{x1D706}}$
and
$a_{\unicode[STIX]{x1D706}}$
and
 $a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
agree in the colimit
$a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
agree in the colimit
 $F(Y)$
, possibly making
$F(Y)$
, possibly making
 $\unicode[STIX]{x1D707}$
smaller again, we can assume
$\unicode[STIX]{x1D707}$
smaller again, we can assume
 $a_{\unicode[STIX]{x1D706}}$
and
$a_{\unicode[STIX]{x1D706}}$
and
 $a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
already agree in
$a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }$
already agree in
 $F(X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}})\cong F(X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime })$
. Then it follows from (CdB) that
$F(X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}})\cong F(X_{\unicode[STIX]{x1D707}}\times _{X_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime }}Y_{\unicode[STIX]{x1D6FC}^{\prime }}^{\prime })$
. Then it follows from (CdB) that
 $\operatorname{Tr}_{f_{\unicode[STIX]{x1D706}}}(a_{\unicode[STIX]{x1D706}})$
agrees with
$\operatorname{Tr}_{f_{\unicode[STIX]{x1D706}}}(a_{\unicode[STIX]{x1D706}})$
agrees with
 $\operatorname{Tr}_{f_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }}(a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime })$
in
$\operatorname{Tr}_{f_{\unicode[STIX]{x1D706}^{\prime }}^{\prime }}(a_{\unicode[STIX]{x1D706}^{\prime }}^{\prime })$
in
 $F(X_{\unicode[STIX]{x1D707}})$
, and therefore also in the colimit
$F(X_{\unicode[STIX]{x1D707}})$
, and therefore also in the colimit
 $F(X)$
.
$F(X)$
.(Add) Given
 $f:Y\rightarrow X$
and
$f:Y\rightarrow X$
and
 $f^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
, choose representatives for
$f^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
, choose representatives for
 $Y\rightarrow X\sqcup X^{\prime }$
and
$Y\rightarrow X\sqcup X^{\prime }$
and
 $Y\rightarrow X\sqcup X^{\prime }$
separately. Then (Add) follows.
$Y\rightarrow X\sqcup X^{\prime }$
separately. Then (Add) follows.(Fon) Given
 $g:W\rightarrow Y$
and
$g:W\rightarrow Y$
and
 $f:Y\rightarrow X$
choose a representative for
$f:Y\rightarrow X$
choose a representative for
 $f$
, and then use the system
$f$
, and then use the system
 $\{X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\}$
to choose a representative for
$\{X_{\unicode[STIX]{x1D706}}\times _{X_{\unicode[STIX]{x1D6FC}}}Y_{\unicode[STIX]{x1D6FC}}\}$
to choose a representative for
 $g$
. Then (Fon) follows.
$g$
. Then (Fon) follows.(CdB) Choose a representative for
 $f$
, then descend
$f$
, then descend
 $W$
to
$W$
to
 $(X_{\unicode[STIX]{x1D706}})$
using [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii)].
$(X_{\unicode[STIX]{x1D706}})$
using [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii)].(Deg) is clear.
(7) If
 $f:T^{\prime }\rightarrow T$
is a finitely presented universal homeomorphism in
$f:T^{\prime }\rightarrow T$
is a finitely presented universal homeomorphism in
 $\mathsf{SCH}_{S}$
, then there exists some
$\mathsf{SCH}_{S}$
, then there exists some
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6EC}$
, and a universal homeomorphism
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6EC}$
, and a universal homeomorphism
 $f_{\unicode[STIX]{x1D6FC}}:T_{\unicode[STIX]{x1D6FC}}^{\prime }\rightarrow T_{\unicode[STIX]{x1D6FC}}$
in
$f_{\unicode[STIX]{x1D6FC}}:T_{\unicode[STIX]{x1D6FC}}^{\prime }\rightarrow T_{\unicode[STIX]{x1D6FC}}$
in
 $\mathsf{Sch}_{S}$
, such that
$\mathsf{Sch}_{S}$
, such that
 $f=T\times _{T_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}}$
, [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii), Theorem 8.10.5(vi)(vii)(viii)], so
$f=T\times _{T_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}}$
, [Reference GrothendieckEGAIV3, Theorem 8.8.2(ii), Theorem 8.10.5(vi)(vii)(viii)], so
 $\unicode[STIX]{x1D704}^{\ast }F(f)=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6FC}}F(T\times _{T_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}})$
is an isomorphism. Note that EGA’s “radiciel” is equivalent to universally injective.
$\unicode[STIX]{x1D704}^{\ast }F(f)=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D6FC}}F(T\times _{T_{\unicode[STIX]{x1D6FC}}}f_{\unicode[STIX]{x1D6FC}})$
is an isomorphism. Note that EGA’s “radiciel” is equivalent to universally injective.Suppose that
 $f:T^{\prime }=\operatorname{Spec}({\mathcal{O}}_{T^{\prime }})\rightarrow \operatorname{Spec}({\mathcal{O}}_{T})=T$
is a universal homeomorphism between affine schemes with finitely many points. Write
$f:T^{\prime }=\operatorname{Spec}({\mathcal{O}}_{T^{\prime }})\rightarrow \operatorname{Spec}({\mathcal{O}}_{T})=T$
is a universal homeomorphism between affine schemes with finitely many points. Write
 ${\mathcal{O}}_{T^{\prime }}=\mathop{\varinjlim }\nolimits_{{\mathcal{O}}_{T}\rightarrow A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{T^{\prime }}}A$
as a filtered colimit of finitely presented
${\mathcal{O}}_{T^{\prime }}=\mathop{\varinjlim }\nolimits_{{\mathcal{O}}_{T}\rightarrow A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{T^{\prime }}}A$
as a filtered colimit of finitely presented
 ${\mathcal{O}}_{T}$
-algebras.
${\mathcal{O}}_{T}$
-algebras.As
 $T^{\prime }\rightarrow T$
is a universal homeomorphism each
$T^{\prime }\rightarrow T$
is a universal homeomorphism each
 $\operatorname{Spec}(\unicode[STIX]{x1D719}(A))\rightarrow T$
is a finite universal homeomorphism, Lemma 7. Also,
$\operatorname{Spec}(\unicode[STIX]{x1D719}(A))\rightarrow T$
is a finite universal homeomorphism, Lemma 7. Also,
 $\unicode[STIX]{x1D719}(A)=\mathop{\varinjlim }\nolimits_{I\subseteq \ker (A\rightarrow \unicode[STIX]{x1D719}(A))}A/I$
is the filtered colimit of the quotients of
$\unicode[STIX]{x1D719}(A)=\mathop{\varinjlim }\nolimits_{I\subseteq \ker (A\rightarrow \unicode[STIX]{x1D719}(A))}A/I$
is the filtered colimit of the quotients of
 $A$
by the finitely generated ideals of the kernel
$A$
by the finitely generated ideals of the kernel
 $K=\ker (A\rightarrow \unicode[STIX]{x1D719}(A))$
. Since
$K=\ker (A\rightarrow \unicode[STIX]{x1D719}(A))$
. Since
 $\operatorname{Spec}(A)$
has finitely many points, we can always find some finitely generated ideal
$\operatorname{Spec}(A)$
has finitely many points, we can always find some finitely generated ideal
 $J$
such that for each
$J$
such that for each
 $J\subseteq I\subseteq K\subseteq A$
the closed immersion
$J\subseteq I\subseteq K\subseteq A$
the closed immersion
 $\operatorname{Spec}(\unicode[STIX]{x1D719}(A))\rightarrow \operatorname{Spec}(A/J)$
is surjective. Hence,
$\operatorname{Spec}(\unicode[STIX]{x1D719}(A))\rightarrow \operatorname{Spec}(A/J)$
is surjective. Hence,
 $f:T^{\prime }\rightarrow T$
is a filtered limit of universal homeomorphisms of finite presentation. We have already seen that
$f:T^{\prime }\rightarrow T$
is a filtered limit of universal homeomorphisms of finite presentation. We have already seen that
 $\unicode[STIX]{x1D704}^{\ast }F$
sends such morphisms to isomorphisms, so
$\unicode[STIX]{x1D704}^{\ast }F$
sends such morphisms to isomorphisms, so
 $\unicode[STIX]{x1D704}^{\ast }F(f)=\varinjlim F(\operatorname{Spec}(A)\rightarrow T)$
is an isomorphism. ◻
$\unicode[STIX]{x1D704}^{\ast }F(f)=\varinjlim F(\operatorname{Spec}(A)\rightarrow T)$
is an isomorphism. ◻