Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Coltoiu, Mihnea
1997.
On Barth’s conjecture concerining .
Nagoya Mathematical Journal,
Vol. 145,
Issue. ,
p.
99.
Colţoiu, Mihnea
2000.
On the relative homology of q-Runge pairs.
Arkiv för Matematik,
Vol. 38,
Issue. 1,
p.
45.
Colţoiu, M.
and
Ruppenthal, J.
2009.
On Hartogs' extension theorem on (n – 1)-complete complex spaces.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2009,
Issue. 637,
Sera, Martin L.
2016.
A Generalization of Takegoshi’s Relative Vanishing Theorem.
The Journal of Geometric Analysis,
Vol. 26,
Issue. 3,
p.
1891.


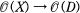 has dense image) iff
has dense image) iff 