Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T03:04:01.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Averaging formula for Nielsen coincidence numbers

Published online by Cambridge University Press:  11 January 2016

Seung Won Kim  and
Jong Bum Lee
Seung Won Kim
Affiliation:
School of Mathematics Korea Institute for Advanced StudySeoul [email protected]
Jong Bum Lee
Affiliation:
Department of Mathematics Sogang UniversitySeoul [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the averaging formula for Nielsen coincidence numbers of pairs of maps (f,g): M→N between closed smooth manifolds of the same dimension. Suppose that G is a normal subgroup of Π = π1(M) with finite index and H is a normal subgroup of Δ = π1(N) with finite index such that 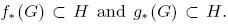Then we investigate the conditions for which the following averaging formula holds

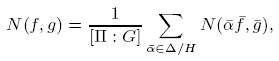
where 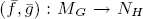is any pair of fixed liftings of (f, g). We prove that the averaging formula holds when M and N are orientable infra-nilmanifolds of the same dimension, and when M = N is a non-orientable infra-nilmanifold with holonomy group ℤ2 and (f, g) admits a pair of liftings 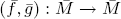on the nil-covering 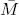of M.

Keywords

55M2057S30
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 186 , 2007 , pp. 69 - 93
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[1] Auslander, L. and Johnson, F. E. A., On a conjecture of C. T. C. Wall, J. London Math. Soc. (2), 14 (1976), 331–332.Google Scholar
[2] Baues, O., Infra-solvmanifolds and rigidity of subgroups in solvable linear algebraic groups, Topology, 43 (2004), 903–924.Google Scholar
[3] Bredon, G. E., Topology and Geometry, Springer-Verlag, New York, 1993.Google Scholar
[4] Brooks, R. and Wong, P., On changing fixed points and coincidences to roots, Proc. Amer. Math. Soc., 115 (1992), 527–533.Google Scholar
[5] Dobreńko, R. and Jezierski, J., The coincidence Nielsen number on non-orientable manifolds, Rocky Mountain J. Math., 23 (1993), 67–85.Google Scholar
[6] Gonçalves, D. L., The coincidence Reidemeister classes of maps on nilmanifolds, Topol. Meth. Nonlin. Anal., 12 (1998), 375–386.Google Scholar
[7] Gonçalves, D. L. and Wong, P., Nilmanifolds are Jiang-type spaces for coincidences, Forum Math., 13 (2001), 133–141.Google Scholar
[8] Guillemin, V. and Pollack, A., Differential topology, Prentice-Hall, Englewood Cliffs, New Jersey, 1974.Google Scholar
[9] Hirsch, M. W., Differential topology, Graduate Text in Mathematics 33, Springer-Verlag, New York, 1976.Google Scholar
[10] Jezierski, J., The Nielsen number product formula for coincidences, Fund. Math., 134 (1990), 183–212.Google Scholar
[11] Jezierski, J., The semi-index product formula, Fund. Math., 140 (1992), 99–120.Google Scholar
[12] Kim, S. W. and Lee, J. B., Anosov theorem for coincidences on nilmanifolds, Fund. Math., 185 (2005), no. 3, 247–259.Google Scholar
[13] Kim, S. W., Lee, J. B. and Lee, K. B., Averaging formula for Nielsen numbers, Nagoya Math. J., 178 (2005), 37–53.Google Scholar
[14] Lee, J. B. and Lee, K. B., Lefschetz numbers for continuous maps, and periods for expanding maps on infra-nilmanifolds, J. Geom. Phys., 56 (2006), 2011–2023.Google Scholar
[15] Lee, K. B. and Raymond, F., Rigidity of almost crystallographic groups, Contemporary Math. Amer. Math. Soc., 44 (1985), 73–78.Google Scholar
[16] McCord, C. K., Estimating Nielsen numbers on infrasolvmanifolds, Pacific J. Math., 154 (1992), 345–368.Google Scholar
[17] Schirmer, H., Mindestzahlen von Koinzidenpunkten, J. Reine Angew. Math., 194 (1955), 21–39.Google Scholar
[18] Vendrùscolo, D., Coincidence classes in nonorientable manifolds, Fixed Point Theory Appl. 2006, Special Issue, Art. ID 68513, 9 pp.Google Scholar
[19] Wong, P., Reidemeister number, Hirsch rank, coincidence on polycyclic groups and solvmanifolds, J. reine angew. Math., 524 (2000), 185–204.Google Scholar