No CrossRef data available.
Article contents
Algebraic threefolds with two extremal morphisms
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In [3] Mori gives a description of all extremal rays (extremal morphisms) arising on a smooth projective threefold with a numerically non-effective canonical bundle. Generally speaking, every smooth projective threefold V with a numerically non-effective canonical class Kv admits an extremal morphism π: V— → Y. The assumption that V admits a non-trivial pair of extremal morph-isms
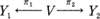
imposes strong conditions on V. This is the essence of the Theorem 1.5 of the present work. In particular, we obtain a description of the threefolds which admit two biregular structures of conic bundles over non-singular surfaces S1 = Y1 and S2 = Y2. By the results of §3 the surfaces Sl and S2 must be either ruled surfaces with isomorphic basic curves, or S1 ≈ S2 ≈ P2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1993
References
[2]
Kulikov, V.S., Degenerations of K3-surfaces and Enriques surfaces, Math. USSR Izvestija, Vol. 41, No. 5 (1977), 1008–1042 (in Russian).Google Scholar
[3]
Mori, S., Threefolds whose canonical bundles are not numerically effective, Ann. of Math., 116 (1982), 133–176.Google Scholar
[4]
Mori, S., Mukai, S., On Fano 3-folds with B2
≥ 2, Adv. St. in Pure Math., Vol.1-Algebraic Varieties and Analytic Varieties, Kinokuniya Comp. LTD (1983), 101–129.Google Scholar
[5]
Sato, E., Varieties which have two projective space bundle structures, J. Math. Kyoto Univ., 25 (1985), 445–457.Google Scholar
You have
Access