Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:42:26.650Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic singularities have maximal reductive automorphism groups

Published online by Cambridge University Press:  22 January 2016

Herwig Hauser  and
Gerd Müller
Herwig Hauser
Affiliation:
Institut für Mathematik Universität Innsbruck, Technikerstr. 25 A-6020 Innsbruck, Austria
Gerd Müller
Affiliation:
Fachbereich Mathematik Universität Mainz, Saarstr. 21 D-6500 Mainz, Federal Republic of Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X = On/i be an analytic singularity where ṫ is an ideal of the C-algebra On of germs of analytic functions on (Cn, 0). Let 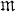denote the maximal ideal of X and A = Aut X its group of automorphisms. An abstract subgroup 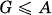equipped with the structure of an algebraic group is called algebraic subgroup of A if the natural representations of G on all “higher cotangent spaces” 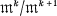are rational. Let π be the representation of A on the first cotangent space 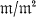and A1 = π(A).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 113 , March 1989 , pp. 181 - 186
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1989

References

[1] Artin, M., Algebraic approximation of structures over complete local rings, Publ. Math. Inst. Hautes Etud. Sci., 36 (1969), 23–58.Google Scholar
[2] Artin, M., Construction techniques for algebraic spaces, Actes Congrès Intern. Math. 1970, tome 1, pp. 419–423.Google Scholar
[3] Becker, J., Denef, J. and Lipshitz, L., The approximation property for some 5- dimensional Henselian rings, Trans. Amer. Math. Soc., 276 (1983), 301–309.CrossRefGoogle Scholar
[4] Bierstone, E. and Milman, P., Invariant solutions of analytic equations, Enseign. Math., 25 (1979), 115–130.Google Scholar
[5] Bingener, J. and Flenner, H., Einige Beispiele nichtalgebraischer Singularitáten, J. Reine Angew. Math., 305 (1979), 182–194.Google Scholar
[6] Gabriélov, A. M., Formal relations between analytic functions, Funct. Anal. Appl., 5 (1971), 318–319.Google Scholar
[7] Hochschild, G. P., Basic theory of algebraic groups and Lie algebras, Springer, 1981.Google Scholar
[8] Kaup, W., Einige Bemerkungen über Automorphismengruppen von Stellenringen, Bayer. Akad. Wiss. Math.-Natur. Kl. Sitzungsber., 1967 (1968), 43–50.Google Scholar
[9] Müller, G., Reduktive Automorphismengruppen analytischer C-Algebren, J. Reine Angew. Math., 364 (1986), 26–34.Google Scholar
[10] Popescu, D., General Néron desingularization and approximation, Nagoya Math. J., 104 (1986), 85–115.Google Scholar
[11] Rotthaus, C., On the approximation property of excellent rings, Invent. Math., 88 (1987), 39–63.CrossRefGoogle Scholar
[12] Saito, K., Quasihomogene isolierte Singularitäten von Hyperflächen, Invent. Math., 14 (1971), 123–142.Google Scholar
[13] Springer, T. A., Invariant theory, Springer, 1977.Google Scholar