Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Muñoz, J.
Muriel, F.J.
and
Rodrı́guez, J.
2001.
A Remark on Goldschmidt's Theorem on Formal Integrability.
Journal of Mathematical Analysis and Applications,
Vol. 254,
Issue. 1,
p.
275.
Kolář, Ivan
and
Mikulski, Włodyimierz M.
2003.
Contact Elements on Fibered Manifolds.
Czechoslovak Mathematical Journal,
Vol. 53,
Issue. 4,
p.
1017.
Doupovec, Miroslav
2005.
On the Underlying Lower Order Bundle Functors.
Czechoslovak Mathematical Journal,
Vol. 55,
Issue. 4,
p.
901.
Kolář, Ivan
2008.
Handbook of Global Analysis.
p.
625.
Sultanov, A. Ya.
2010.
Derivations of linear algebras and linear connections.
Journal of Mathematical Sciences,
Vol. 169,
Issue. 3,
p.
362.
Sultanov, A. Ya.
2012.
Holomorphic affine vector fields on weil bundles.
Mathematical Notes,
Vol. 91,
Issue. 5-6,
p.
847.
Shurygin, V. V.
2012.
Lifts of Poisson structures to Weil bundle.
Lobachevskii Journal of Mathematics,
Vol. 33,
Issue. 1,
p.
75.
Султанов, Адгам Яхиевич
and
Sultanov, Adgam Yakhievich
2012.
Голоморфные аффинные векторные поля на расслоениях Вейля.
Математические заметки,
Vol. 91,
Issue. 6,
p.
896.
Kolář, Ivan
2013.
On the natural transformations of Weil bundles.
Archivum Mathematicum,
p.
303.
Ivičič, Vojtěch
and
Kureš, Miroslav
2016.
Two general examples of Weil algebras having the group of automorphisms connected.
International Journal of Geometric Methods in Modern Physics,
Vol. 13,
Issue. 03,
p.
1650035.
Sultanov, A. Ya.
and
Monakhova, O. A.
2020.
Affine Transformations in Bundles.
Journal of Mathematical Sciences,
Vol. 245,
Issue. 5,
p.
601.
Mialebama Bouesso, Andre S. E.
Lekaka Ndinga, Franck R.
Bossoto, Basile G. R.
and
Luciano, Gaetano
2023.
Differential Forms and Cohomology on Weil Bundles.
Journal of Mathematics,
Vol. 2023,
Issue. ,
p.
1.
Mialebama Bouesso, Andre S. E.
Mekiya Moutabanza, F.
and
Bayeni Mitoueni, Jude R.
2024.
Symplectic structure and applications on Weil bundles.
Afrika Matematika,
Vol. 35,
Issue. 1,


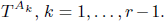 We deduce that
We deduce that 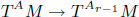 is an affine bundle for every manifold
is an affine bundle for every manifold 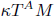 of contact elements of type
of contact elements of type 