Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-25T01:37:43.571Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME RESULTS ON THE TOPOLOGY OF ALGEBRAIC SURFACES

Part of: Holomorphic convexity Surfaces and higher-dimensional varieties (Co)homology theory

Published online by Cambridge University Press:  17 February 2025

RAJENDRA V. GURJAR Open the ORCID record for RAJENDRA V. GURJAR [Opens in a new window] ,
SUDARSHAN R. GURJAR Open the ORCID record for SUDARSHAN R. GURJAR [Opens in a new window]  and
SOUMYADIP THANDAR Open the ORCID record for SOUMYADIP THANDAR [Opens in a new window]
RAJENDRA V. GURJAR*
Affiliation:
Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai, 400 076 India
SUDARSHAN R. GURJAR
Affiliation:
Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai, 400 076 India [email protected]
SOUMYADIP THANDAR
Affiliation:
School of Mathematics Tata Institute of Fundamental Research Mumbai Mumbai, 400 005 India [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we discuss the topology of varieties over 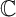$\mathbb {C}$, viz., their homology and homotopy groups. We show that the fundamental group of a quasi-projective variety has negative deficiency under a certain hypothesis on its second homology and therefore a large class of groups cannot arise as fundamental groups of varieties. For a smooth projective surface admitting a fibration over a curve, we give a detailed analysis of the homology and homotopy groups of their universal cover via a case-by-case analysis, depending on the nature of the singular fibers. For smooth, projective surfaces whose universal cover is holomorphically convex (conjecturally always true), we show that the second and third homotopy groups are free abelian, often of infinite rank.

Keywords

quasi-projective varietyhomotopy groupsholomorphic convexity

MSC classification

Primary: 14F35: Homotopy theory; fundamental groups
Secondary: 14F45: Topological properties 14J10: Families, moduli, classification 32E05: Holomorphically convex complex spaces, reduction theory
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreotti, A. and Frankel, T., The Lefschetz theorem on hyperplane sections , Ann. of Math. (2). 69 (1959), 713–717.CrossRefGoogle Scholar
Arkowitz, M., Introduction to homotopy theory, Universitext, Springer, New York, 2011.CrossRefGoogle Scholar
Basu, S., Of Sullivan models, Massey products, and twisted Pontrjagin products , J. Homotopy Relat. Struct. 10 (2015), no.2, 239–273.CrossRefGoogle Scholar
Basu, S. and Basu, S., Homotopy groups and periodic geodesics of closed 4-manifolds , Internat. J. Math. 26 (2015) no. 8, 1550059, 34.CrossRefGoogle Scholar
Bieri, R., Cornulier, Y., Guyot, L. and Strebel, R., Infinite presentability of groups and condensation , J. Inst. Math. Jussieu 13 (2014) no. 4, 811–848.CrossRefGoogle Scholar
Biswas, I. and Mj, M., ${H}_1$ -semistability for projective groups , Math. Proc. Cambridge Philos. Soc. 162 (2017), no. 1, 89–100.CrossRefGoogle Scholar
Colţoiu, M. and Mihalache, N., On the homology groups of Stein spaces and Runge pairs , J. Reine Angew. Math. 371 (1986), 216–220.Google Scholar
Eyssidieux, P., Katzarkov, L., Pantev, T. and Ramachandran, M., Linear Shafarevich conjecture , Ann. of Math. (2), 176 (2012) no. 3, 1545–1581.CrossRefGoogle Scholar
Friedman, R. and Morgan, J. W., Smooth four-manifolds and complex surfaces, Vol. 27, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], Springer-Verlag, Berlin, 1994.CrossRefGoogle Scholar
Ganea, T., Induced fibrations and cofibrations , Trans. Amer. Math. Soc. 127 (1967), 442–459.CrossRefGoogle Scholar
Gardam, G., Finite groups of arbitrary deficiency , Bull. Lond. Math. Soc. 49 (2017) no. 6, 1100–1104.CrossRefGoogle Scholar
Gurjar, R. V., A new proof of Suzuki’s formula , Proc. Indian Acad. Sci. Math. Sci. 107 (1997) no. 3, 237–242.CrossRefGoogle Scholar
Gurjar, R. V., Two remarks on the topology of projective surfaces , Math. Ann. 328 (2004) no. 4, 701–706.CrossRefGoogle Scholar
Gurjar, R. V., Gurjar, S. R. and Hajra, B., Eilenberg-MacLane spaces in algebraic surface theory , Geom. Dedicata, 217 (2023) no. 2, Paper No. 31, 27.CrossRefGoogle Scholar
Gurjar, R. V. and Kolte, S., Fundamental group of some genus-2 fibrations and applications , Internat. J. Math. 23 (2012) no. 8, 1250080, 20 pp.CrossRefGoogle Scholar
Gurjar, R. V., Paul, S. and Purnaprajna, B. P., On the fundamental group of hyperelliptic fibrations and some applications , Invent. Math., 186 (2011), no. 2, 237–254.CrossRefGoogle Scholar
Gurjar, R. V. and Shastri, A. R., Covering spaces of an elliptic surface , Compositio Math. 54 (1985) no. 1, 95–104.Google Scholar
Gurjar, S. R. and Pokale, P., Second homotopy groups of compact complex surfaces of non-general type , Bull. Sci. Math. 182 (2023), Paper No. 103208, 21.CrossRefGoogle Scholar
Hamm, H. A., Zur Homotopietyp Steinscher Räume , J. Reine Angew. Math. 338 (1983), 121–135.CrossRefGoogle Scholar
Hatcher, A., Algebraic topology, Cambridge University Press, Cambridge, 2002.Google Scholar
Hilton, P. J., On the homotopy groups of the union of spheres , J. London Math. Soc. 30 (1955), 154–172.CrossRefGoogle Scholar
Lefschetz, S. L’analysis situs et la géométrie algébrique, Gauthier-Villars, Paris, 1950.Google Scholar
Milnor, J., Morse theory, Annals of Mathematics Studies, No. 51, Princeton University Press, Princeton, NJ, 1963. Based on lecture notes by M. Spivak and R. Wells.CrossRefGoogle Scholar
Nori, M. V., Zariski’s conjecture and related problems , Ann. Sci. École Norm. Sup. (4) 16 (1983), no. 2, 305–344.CrossRefGoogle Scholar
Serre, J.-P. “Quelques problèmes globaux relatifs aux variétés de Stein” in Colloque sur les fonctions de plusieurs variables, tenu à Bruxelles, Georges Thone, Liège; Masson & Cie, Paris, 1953, pp. 57–68.Google Scholar
Shafarevich, I. R., Basic algebraic geometry, Die Grundlehren der mathematischen Wissenschaften, Band Vol. 213, Springer-Verlag, New York, 1974, Translated from the Russian by K. A. Hirsch.CrossRefGoogle Scholar
Sullivan, D., Infinitesimal computations in topology , Inst. Hautes Études Sci. Publ. Math. 47 (1977), 269–331 (1978).CrossRefGoogle Scholar
Suzuki, M., Sur les opérations holomorphes du groupe additif complexe sur l’espace de deux variables complexes , Ann. Sci. École Norm. Sup. (4). 10 (1977), no. 4, 517–546.CrossRefGoogle Scholar