Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T13:14:34.431Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CANONICAL BASES AND INDUCTION OF 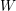$W$-GRAPHS

Part of: Representation theory of groups Hopf algebras, quantum groups and related topics Special aspects of infinite or finite groups

Published online by Cambridge University Press:  17 July 2018

JOHANNES HAHN
JOHANNES HAHN*
Affiliation:
Friedrich Schiller University Jena, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A canonical basis in the sense of Lusztig is a basis of a free module over a ring of Laurent polynomials that is invariant under a certain semilinear involution and is obtained from a fixed “standard basis” through a triangular base change matrix with polynomial entries whose constant terms equal the identity matrix. Among the better known examples of canonical bases are the Kazhdan–Lusztig basis of Iwahori–Hecke algebras (see Kazhdan and Lusztig, Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184), Lusztig’s canonical basis of quantum groups (see Lusztig, Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3(2) (1990), 447–498) and the Howlett–Yin basis of induced 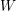$W$-graph modules (see Howlett and Yin, Inducing W-graphs I, Math. Z. 244(2) (2003), 415–431; Inducing W-graphs II, Manuscripta Math. 115(4) (2004), 495–511). This paper has two major theoretical goals: first to show that having bases is superfluous in the sense that canonicalization can be generalized to nonfree modules. This construction is functorial in the appropriate sense. The second goal is to show that Howlett–Yin induction of 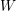$W$-graphs is well-behaved a functor between module categories of 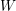$W$-graph algebras that satisfies various properties one hopes for when a functor is called “induction,” for example transitivity and a Mackey theorem.

MSC classification

Primary: 20C08: Hecke algebras and their representations 20F55: Reflection and Coxeter groups 16T20: Ring-theoretic aspects of quantum groups
Type
Article
Information
Nagoya Mathematical Journal , Volume 239 , September 2020 , pp. 1 - 41
Check for updates
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Couillens, M., Généralisation parabolique des polynômes et des bases de kazhdan–lusztig, J. Algebra 213(2) (1999), 687–720.10.1006/jabr.1998.7645Google Scholar
Deodhar, V. V., Some characterizations of Bruhat ordering on a Coxeter group and determination of the relative Möbius function, Invent. Math. 39(2) (1977), 187–198.10.1007/BF01390109Google Scholar
Deodhar, V. V., On some geometric aspects of Bruhat orderings II. The parabolic analogue of Kazhdan–Lusztig polynomials, J. Algebra 111(2) (1987), 483–506.10.1016/0021-8693(87)90232-8Google Scholar
Eilenberg, S., Abstract description of some basic functors, J. Indian Math. Soc 24 (1960), 231–234.Google Scholar
Geck, M., On the induction of Kazhdan–Lusztig cells, Bull. Lond. Math. Soc. 35(5) (2003), 608–614.10.1112/S0024609303002236Google Scholar
Geck, M., PyCox: computing with (finite) Coxeter groups and Iwahori–Hecke algebras, LMS J. Comput. Math. 15 (2012), 231–256.10.1112/S1461157012001064Google Scholar
Geck, M. and Jacon, N., Representations of Hecke Algebras at Roots of Unity, Algebra and Applications, Springer, 2011.10.1007/978-0-85729-716-7Google Scholar
Geck, M. and Pfeiffer, G., Characters of Finite Coxeter Groups and Iwahori–Hecke Algebras, London Mathematical Society Monographs, Clarendon Press, 2000.Google Scholar
Gyoja, A., On the existence of a W-graph for an irreducible representation of a Coxeter group, J. Algebra 84 (1984), 422–438.Google Scholar
Hahn, J., Gyojas W-graph-algebra und zelluläre Struktur von Iwahori–Hecke-algebren. PhD thesis, Friedrich–Schiller-Universität Jena, Nov. 2013. Also available at arXiv:abs/1801.08834.Google Scholar
Hahn, J., W-graphs and Goja’s W-graph algebra, Nagoya Math. J. 226 (2017), 1–43.Google Scholar
Howlett, R. B. and Yin, Y., Inducing W-graphs I, Math. Z. 244(2) (2003), 415–431.10.1007/s00209-003-0507-1Google Scholar
Howlett, R. B. and Yin, Y., Inducing W-graphs II, Manuscripta Math. 115(4) (2004), 495–511.10.1007/s00229-004-0508-3Google Scholar
Kashiwara, Masaki, Crystalizing the q-analogue of universal enveloping algebras, Commun. Math. Phys. 133(2) (1990), 249–260.Google Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184.Google Scholar
Lusztig, G., Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3(2) (1990), 447–498.Google Scholar
Lusztig, George, Hecke Algebras with Unequal Parameters, CRM Monograph Series, American Mathematical Society, 2003.10.1090/crmm/018Google Scholar
Matsumoto, H., Générateurs et relations des groupes de Weyl généralisés, C. R. Acad. Sci. Paris 258 (1964), 3419–3422.Google Scholar
Watts, C. E., Intrinsic characterizations of some additive functors, Proc. Amer. Math. Soc. 11(1) (1960), 5–8.Google Scholar