Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-01T01:56:50.188Z Has data issue: false hasContentIssue false
  • English
  • Français

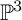NEW MODULI SPACES OF ONE-DIMENSIONAL SHEAVES ON $\mathbb {P}^3$

Part of: Families, fibrations

Published online by Cambridge University Press:  18 September 2023

DAPENG MU Open the ORCID record for DAPENG MU [Opens in a new window]
DAPENG MU*
Affiliation:
Instituto de Matemática, Estatística e Computação Científica (IMECC) Universidade Estadual de Campinas (Unicamp) Room 327-328, IMECC, UNICAMP, Rua Sérgio Buarque de Holanda 651 13083-859 Campinas, SP Brazil
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a one-dimensional family of Bridgeland stability conditions on 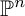$\mathbb {P}^n$, named “Euler” stability condition. We conjecture that the “Euler” stability condition converges to Gieseker stability for coherent sheaves. Here, we focus on 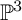${\mathbb P}^3$, first identifying Euler stability conditions with double-tilt stability conditions, and then we consider moduli of one-dimensional sheaves, proving some asymptotic results, boundedness for walls, and then explicitly computing walls and wall-crossings for sheaves supported on rational curves of degrees 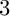$3$ and $4$.

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles
Type
Article
Information
Nagoya Mathematical Journal , Volume 254 , June 2024 , pp. 265 - 314
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

D.M. is currently supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (Grant No. 2020/03499-0).

References

Private conversations with Prof. Dr. Aaron Bertram. Google Scholar
Arcara, D. and Bertram, A., Bridgeland-stable moduli spaces for K-trivial surfaces , J. Eur. Math. Soc. 15 (2013), 1–38.CrossRefGoogle Scholar
Arcara, D., Bertram, A., Coskun, I., and Huizenga, J., The minimal model program for the Hilbert scheme of points on ${\mathbb{P}}^2$ and Bridgeland stability, Adv. Math. 235 (2013), 580–626.CrossRefGoogle Scholar
Bayer, A. and Macrì, E., The space of stability conditions on the local projective plane , Duke Math. J. 160 (2011), 263–322.CrossRefGoogle Scholar
Bayer, A., Macrì, E., and Stellari, P., The space of stability conditions on abelian threefolds, and on some Calabi–Yau threefolds , Invent. Math. 206 (2016), 869–933.10.1007/s00222-016-0665-5CrossRefGoogle Scholar
Bayer, A., Macrì, E., and Toda, Y., Bridgeland stability conditions on threefolds I: Bogomolov–Gieseker type inequalities , J. Algebraic Geom. 23 (2013), 117–163.10.1090/S1056-3911-2013-00617-7CrossRefGoogle Scholar
Beilinson, A., Bernstein, J., and Deligne, P., Faisceaux perverse , Astérisque 100 (1982), 1–172.Google Scholar
Bernardara, M., Macrì, E., Schmidt, B., and Zhao, X., Bridgeland stability conditions on Fano threefolds , Épijournal de Géométrie Algébrique 1 (2017), 15–38.CrossRefGoogle Scholar
Bridgeland, T., Stability conditions on triangulated categories , Ann. of Math. 166 (2007), 317–345.CrossRefGoogle Scholar
Bridgeland, T., Stability conditions on K3 surfaces , Duke Math. J. 141 (2008), 241–291.CrossRefGoogle Scholar
Freiermuth, H. G., On the Moduli Space ${M}_P({\mathbb{P}}^3)$ of Semi-Stable Sheaves on ${\mathbb{P}}^3$ with Hilbert Polynomial $P(m)=3m+1$ , Diplomarbeit, Universutät Kaiserslautern, Kaiserslautern, 2000.Google Scholar
Freiermuth, H. G. and Trautmann, G., On the moduli scheme of stable sheaves supported on cubic space curves , Amer. J. Math. 126 (2004), 363–393.CrossRefGoogle Scholar
Gallardo, P., Huerta, C. L., and Schmidt, B., Families of elliptic curves in ${\mathbb{P}}^3$ and Bridgeland stability , Michigan Math. J. 67 (2018), 787–813.CrossRefGoogle Scholar
Happel, D., Reiten, I., and Smalø, S. O., Tilting in abelian categories and quasitilted algebras , Mem. Amer. Math. Soc. 120 (1996), 1–88.Google Scholar
Huybrechts, D., Introduction to stability conditions , Moduli Spaces 411 (2014), 179–229.10.1017/CBO9781107279544.005CrossRefGoogle Scholar
Jardim, M., Maciocia, A., and Martinez, C., Vertical asymptotics for Bridgeland stability conditions on 3-folds, Int. Math. Res. Not. 2023 (17), 14699–14751.Google Scholar
King, A. D., Moduli of representations of finite dimensional algebras , Q. J. Math. 45 (1994), 515–530.10.1093/qmath/45.4.515CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry I, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas, 3rd Series, A Series of Modern Surveys in Mathematics], Springer, Berlin, 2004.CrossRefGoogle Scholar
Le Potier, J., Faisceaux semi-stables de dimension 1 sur le plan projectif , Rev. Roumaine Math. Pures Appl. 38 (1993), 635–678.Google Scholar
Li, C., Stability conditions on Fano threefolds of Picard number 1 , J. Eur. Math. Soc. (JEMS) 21 (2019), 709–726.CrossRefGoogle Scholar
Maciocia, A., Computing the walls associated to Bridgeland stability conditions on projective surfaces , Asian J. Math. 18 (2014), 263–279.CrossRefGoogle Scholar
Maciocia, A. and Jardim, M., Walls and asymptotics for Bridgeland stability conditions on 3-folds , Épijournal de Géométrie Algébrique 6 (2022), 655–715.Google Scholar
Maciocia, A. and Piyaratne, D., Fourier–Mukai transforms and Bridgeland stability conditions on abelian threefolds, Algebr. Geom. 2 (2015), 270–297.CrossRefGoogle Scholar
Maciocia, A. and Piyaratne, D., Fourier–Mukai transforms and Bridgeland stability conditions on abelian threefolds II , Internat. J. Math. 27 (2016), 1650007.CrossRefGoogle Scholar
Macrì, E., Stability conditions on curves , Math. Res. Lett. 14 (2007), 657–672.CrossRefGoogle Scholar
Macrì, E., A generalized Bogomolov–Gieseker inequality for the three-dimensional projective space , Algebra Number Theory 8 (2014), 173–190.CrossRefGoogle Scholar
Macrì, E. and Schmidt, B., Lectures on Bridgeland Stability, Lecture Notes of the Unione Matematica Italiana, Springer International Publishing, Cham, 2017, 139–211.CrossRefGoogle Scholar
Maican, M., A duality result for moduli spaces of semistable sheaves supported on projective curves , Rend. Semin. Mat. Univ. Padova 123 (2010), 55–68.CrossRefGoogle Scholar
Martinez, C., Duality, Bridgeland wall-crossing and flip of secant varieties. , Internat. J. Math. 28 (2017), 1750011.CrossRefGoogle Scholar
Piyaratne, D. and Toda, Y., Moduli of Bridgeland semistable objects on 3-folds and Donaldson–Thomas invariants , J. Reine Angew. Math. 747 (2019), 175–219.CrossRefGoogle Scholar
Pretti, V., Zero rank asymptotic Bridgeland stability , J. Geom. Phys. 182 (2022), 104668.CrossRefGoogle Scholar
Schmidt, B., A generalized Bogomolov–Gieseker inequality for the smooth quadric threefold , Bull. Lond. Math. Soc. 46 (2014), 915–923.CrossRefGoogle Scholar
Schmidt, B., Bridgeland stability on threefolds: Some wall crossings , J. Algebraic Geom. 29 (2020), 247–283.CrossRefGoogle Scholar
Toda, Y., Limit stable objects on Calabi–Yau 3-folds , Duke Math. J. 149 (2009), 157–208.CrossRefGoogle Scholar
Xia, B., Hilbert scheme of twisted cubics as a simple wall-crossing , Trans. Amer. Math. Soc 370 (2018), 5535–5559.CrossRefGoogle Scholar