Article contents
LIE ALGEBRA MODULES WHICH ARE LOCALLY FINITE AND WITH FINITE MULTIPLICITIES OVER THE SEMISIMPLE PART
Published online by Cambridge University Press: 02 August 2021
Abstract
For a finite-dimensional Lie algebra 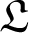 $\mathfrak {L}$
over
$\mathfrak {L}$
over  $\mathbb {C}$
with a fixed Levi decomposition
$\mathbb {C}$
with a fixed Levi decomposition 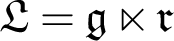 $\mathfrak {L} = \mathfrak {g} \ltimes \mathfrak {r}$
, where
$\mathfrak {L} = \mathfrak {g} \ltimes \mathfrak {r}$
, where 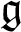 $\mathfrak {g}$
is semisimple, we investigate
$\mathfrak {g}$
is semisimple, we investigate 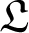 $\mathfrak {L}$
-modules which decompose, as
$\mathfrak {L}$
-modules which decompose, as 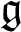 $\mathfrak {g}$
-modules, into a direct sum of simple finite-dimensional
$\mathfrak {g}$
-modules, into a direct sum of simple finite-dimensional 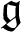 $\mathfrak {g}$
-modules with finite multiplicities. We call such modules
$\mathfrak {g}$
-modules with finite multiplicities. We call such modules 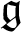 $\mathfrak {g}$
-Harish-Chandra modules. We give a complete classification of simple
$\mathfrak {g}$
-Harish-Chandra modules. We give a complete classification of simple 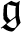 $\mathfrak {g}$
-Harish-Chandra modules for the Takiff Lie algebra associated to
$\mathfrak {g}$
-Harish-Chandra modules for the Takiff Lie algebra associated to 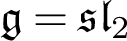 $\mathfrak {g} = \mathfrak {sl}_2$
, and for the Schrödinger Lie algebra, and obtain some partial results in other cases. An adapted version of Enright’s and Arkhipov’s completion functors plays a crucial role in our arguments. Moreover, we calculate the first extension groups of infinite-dimensional simple
$\mathfrak {g} = \mathfrak {sl}_2$
, and for the Schrödinger Lie algebra, and obtain some partial results in other cases. An adapted version of Enright’s and Arkhipov’s completion functors plays a crucial role in our arguments. Moreover, we calculate the first extension groups of infinite-dimensional simple 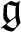 $\mathfrak {g}$
-Harish-Chandra modules and their annihilators in the universal enveloping algebra, for the Takiff
$\mathfrak {g}$
-Harish-Chandra modules and their annihilators in the universal enveloping algebra, for the Takiff 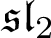 $\mathfrak {sl}_2$
and the Schrödinger Lie algebra. In the general case, we give a sufficient condition for the existence of infinite-dimensional simple
$\mathfrak {sl}_2$
and the Schrödinger Lie algebra. In the general case, we give a sufficient condition for the existence of infinite-dimensional simple 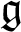 $\mathfrak {g}$
-Harish-Chandra modules.
$\mathfrak {g}$
-Harish-Chandra modules.
MSC classification
- Type
- Article
- Information
- Copyright
- © (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
This research was partially supported by the Swedish Research Council, Göran Gustafsson Stiftelse and Vergstiftelsen. Rafael Mrđen was also partially supported by the QuantiXLie Center of Excellence grant no. KK.01.1.1.01.0004 funded by the European Regional Development Fund.
References
- 3
- Cited by



