In this paper, we perform a detailed spectral study of the liberation process associated with two symmetries of arbitrary ranks: 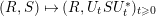$(R,S)\mapsto (R,U_{t}SU_{t}^{\ast })_{t\geqslant 0}$, where $(U_{t})_{t\geqslant 0}$ is a free unitary Brownian motion freely independent from 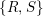$\{R,S\}$. Our main tool is free stochastic calculus which allows to derive a partial differential equation (PDE) for the Herglotz transform of the unitary process defined by 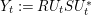$Y_{t}:=RU_{t}SU_{t}^{\ast }$. It turns out that this is exactly the PDE governing the flow of an analytic function transform of the spectral measure of the operator 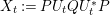$X_{t}:=PU_{t}QU_{t}^{\ast }P$ where 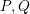$P,Q$ are the orthogonal projections associated to 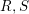$R,S$. Next, we relate the two spectral measures of 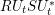$RU_{t}SU_{t}^{\ast }$ and of 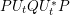$PU_{t}QU_{t}^{\ast }P$ via their moment sequences and use this relationship to develop a theory of subordination for the boundary values of the Herglotz transform. In particular, we explicitly compute the subordinate function and extend its inverse continuously to the unit circle. As an application, we prove the identity 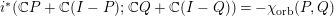$i^{\ast }(\mathbb{C}P+\mathbb{C}(I-P);\mathbb{C}Q+\mathbb{C}(I-Q))=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.