No CrossRef data available.
Published online by Cambridge University Press: 04 December 2020
Let C be a hyperelliptic curve of genus 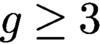 $g \geq 3$
. In this paper, we give a new geometric description of the theta map for moduli spaces of rank 2 semistable vector bundles on C with trivial determinant. In order to do this, we describe a fibration of (a birational model of) the moduli space, whose fibers are GIT quotients
$g \geq 3$
. In this paper, we give a new geometric description of the theta map for moduli spaces of rank 2 semistable vector bundles on C with trivial determinant. In order to do this, we describe a fibration of (a birational model of) the moduli space, whose fibers are GIT quotients 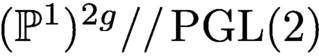 $(\mathbb {P}^1)^{2g}//\text {PGL(2)}$
. Then, we identify the restriction of the theta map to these GIT quotients with some explicit degree 2 osculating projection. As a corollary of this construction, we obtain a birational inclusion of a fibration in Kummer
$(\mathbb {P}^1)^{2g}//\text {PGL(2)}$
. Then, we identify the restriction of the theta map to these GIT quotients with some explicit degree 2 osculating projection. As a corollary of this construction, we obtain a birational inclusion of a fibration in Kummer 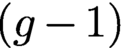 $(g-1)$
-varieties over
$(g-1)$
-varieties over 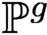 $\mathbb {P}^g$
inside the ramification locus of the theta map.
$\mathbb {P}^g$
inside the ramification locus of the theta map.
Michele Bolognesi is member of the research groups GAGC and GNSAGA, whose support is acknowledged.
 ${\mathbf{\mathcal{SU}}}_C(2)$
and the moduli of pointed rational curves
, J. Algebraic Geom. 24 (2015), no. 2, 283–310.CrossRefGoogle Scholar
${\mathbf{\mathcal{SU}}}_C(2)$
and the moduli of pointed rational curves
, J. Algebraic Geom. 24 (2015), no. 2, 283–310.CrossRefGoogle Scholar ${\mathbf{\mathcal{M}}}_{0,2n}^{GIT}$
, Bull. Lond. Math. Soc. 43 (2011), no. 3, 583–596.10.1112/blms/bdq125CrossRefGoogle Scholar
${\mathbf{\mathcal{M}}}_{0,2n}^{GIT}$
, Bull. Lond. Math. Soc. 43 (2011), no. 3, 583–596.10.1112/blms/bdq125CrossRefGoogle Scholar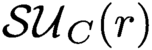 ${\mathbf{\mathcal{SU}}}_C(r)$
, Int. J. Math. 23 (2012), no. 4, 1250037.CrossRefGoogle Scholar
${\mathbf{\mathcal{SU}}}_C(r)$
, Int. J. Math. 23 (2012), no. 4, 1250037.CrossRefGoogle Scholar ${\mathbf{\mathcal{SU}}}_C{\left(2,2d\right)}^s$
is very ample if
${\mathbf{\mathcal{SU}}}_C{\left(2,2d\right)}^s$
is very ample if
 ${\overline{M}}_{0,n}$
, J. Algebraic Geom. 2 (1993), no. 2, 239–262.Google Scholar
${\overline{M}}_{0,n}$
, J. Algebraic Geom. 2 (1993), no. 2, 239–262.Google Scholar ${\overline{M}}_{0,n}$
. In
Handbook of Moduli. volume 25 of Adv. Lect. Math. (ALM)
II, Int. Press, Somerville, MA, 2013, 115–130.Google Scholar
${\overline{M}}_{0,n}$
. In
Handbook of Moduli. volume 25 of Adv. Lect. Math. (ALM)
II, Int. Press, Somerville, MA, 2013, 115–130.Google Scholar