Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T07:09:48.443Z Has data issue: false hasContentIssue false
  • English
  • Français

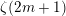GENERALIZED LAMBERT SERIES, RAABE’S COSINE TRANSFORM AND A GENERALIZATION OF RAMANUJAN’S FORMULA FOR $\unicode[STIX]{x1D701}(2m+1)$

Part of: Zeta and $L$-functions: analytic theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  04 October 2018

ATUL DIXIT Open the ORCID record for ATUL DIXIT [Opens in a new window] ,
RAJAT GUPTA ,
RAHUL KUMAR  and
BIBEKANANDA MAJI
ATUL DIXIT
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India email [email protected]
RAJAT GUPTA
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India email [email protected]
RAHUL KUMAR
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India email [email protected]
BIBEKANANDA MAJI
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

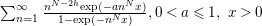A comprehensive study of the generalized Lambert series $\sum _{n=1}^{\infty }\frac{n^{N-2h}\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)},0<a\leqslant 1,~x>0$, 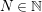$N\in \mathbb{N}$ and 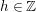$h\in \mathbb{Z}$, is undertaken. Several new transformations of this series are derived using a deep result on Raabe’s cosine transform that we obtain here. Three of these transformations lead to two-parameter generalizations of Ramanujan’s famous formula for $\unicode[STIX]{x1D701}(2m+1)$ for 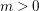$m>0$, the transformation formula for the logarithm of the Dedekind eta function and Wigert’s formula for 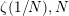$\unicode[STIX]{x1D701}(1/N),N$ even. Numerous important special cases of our transformations are derived, for example, a result generalizing the modular relation between the Eisenstein series 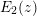$E_{2}(z)$ and 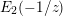$E_{2}(-1/z)$. An identity relating 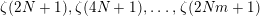$\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$ is obtained for 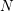$N$ odd and 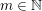$m\in \mathbb{N}$. In particular, this gives a beautiful relation between 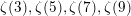$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and 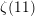$\unicode[STIX]{x1D701}(11)$. New results involving infinite series of hyperbolic functions with 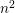$n^{2}$ in their arguments, which are analogous to those of Ramanujan and Klusch, are obtained.

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 11J81: Transcendence (general theory)
Type
Article
Information
Nagoya Mathematical Journal , Volume 239 , September 2020 , pp. 232 - 293
Check for updates
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (eds), Handbook of Mathematical Functions, Dover, New York, 1965.Google Scholar
Apéry, R., Irrationalité de 𝜁(2) et 𝜁(3), Astérisque 61 (1979), 11–13.Google Scholar
Apéry, R., Interpolation de fractions continues et irrationalité de certaines constantes, Bull. Section des Sci. Tome III, Bibliothéque Nationale, Paris, 1981, 37–63.Google Scholar
Apostol, T. M., Modular Functions and Dirichlet Series in Number Theory, 2nd ed. Springer, 1990.10.1007/978-1-4612-0999-7Google Scholar
Apostol, T. M., Introduction to Analytic Number Theory, Springer, New York, 1998.Google Scholar
Ball, K. and Rivoal, T., Irrationalité d’une infinité de valeurs de la fonction zêta aux entiers impairs, Invent. Math. 146(1) (2001), 193–207; (French).10.1007/s002220100168Google Scholar
Berndt, B. C., Modular transformations and generalizations of several formulae of Ramanujan, Rocky Mountain J. Math. 7 (1977), 147–189.10.1216/RMJ-1977-7-1-147Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part II, Springer, New York, 1989.10.1007/978-1-4612-4530-8Google Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III, Springer, New York, 1991.10.1007/978-1-4612-0965-2Google Scholar
Berndt, B. C., Chan, H. H. and Tanigawa, Y., Two Dirichlet series evaluations found on page 196 of Ramanujan’s Lost Notebook, Math. Proc. Cambridge Philos. Soc. 153(2) (2012), 341–360.10.1017/S0305004112000151Google Scholar
Berndt, B. C., Dixit, A., Roy, A. and Zaharescu, A., New pathways and connections in number theory and analysis motivated by two incorrect claims of Ramanujan, Adv. Math. 304 (2017), 809–929.10.1016/j.aim.2016.08.011Google Scholar
Berndt, B. C. and Straub, A., On a secant Dirichlet series and Eichler integrals of Eisenstein series, Math. Z. 284(3–4) (2016), 827–852.10.1007/s00209-016-1675-0Google Scholar
Berndt, B. C. and Straub, A., “Ramanujan’s formula for 𝜁(2n + 1)”, in Exploring the Riemann Zeta Function, (eds. Montgomery, H., Nikeghbali, A. and Rassias, M.) Springer, 2017, 13–34.10.1007/978-3-319-59969-4_2Google Scholar
Boxall, G. J. and Jones, G. O., Algebraic values of certain analytic functions, Int. Math. Res. Not.  IMRN 2015(4) (2015), 1141–1158.10.1093/imrn/rnt239Google Scholar
Bringmann, K., Folsom, A., Ono, K. and Rolen, L., Harmonic Maass Forms and Mock Modular Forms: Theory and Applications, American Mathematical Society, Providence, 2017.10.1090/coll/064Google Scholar
Cassels, J. W. S., Footnote to a note of Davenport and Heilbronn, J. Lond. Math. Soc. (2) 36 (1961), 177–184.10.1112/jlms/s1-36.1.177Google Scholar
Dai, H. H. and Naylor, D., On an asymptotic expansion of Fourier integrals, Proc. R. Soc. Lond. Ser. A 436(1896) (1992), 109–120.Google Scholar
Davenport, H., Multiplicative Number Theory, 3rd ed. Springer, New York, 2000.Google Scholar
Davenport, H. and Heilbronn, H., On the zeros of certain Dirichlet series, I, J. Lond. Math. Soc. (2) 11 (1936), 181–185.10.1112/jlms/s1-11.3.181Google Scholar
Dixit, A., The Laplace transform of the psi function, Proc. Amer. Math. Soc. 138(2) (2010), 593–603.10.1090/S0002-9939-09-10157-0Google Scholar
Dixit, A. and Maji, B., Generalized Lambert series and arithmetic nature of odd zeta values, preprint, 2017, arXiv:1709.00022v3 (submitted for publication).Google Scholar
Dixon, A. L. and Ferrar, W. L., Lattice-point summation formulae, Q. J. Math. 2 (1931), 31–54.Google Scholar
Dixon, A. L. and Ferrar, W. L., Infinite integrals of Bessel functions, Q. J. Math. 1 (1935), 161–174.Google Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F., Higher Transcendental Functions, Bateman Manuscript Project II, McGraw-Hill, New York, 1953.Google Scholar
Erdös, P., On arithmetical properties of Lambert series, J. Indian Math. Soc. (N.S.) 12 (1948), 63–66.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (eds), Table of Integrals, Series, and Products, 8th ed. (eds. Zwillinger, D. and Moll, V. H.) Academic Press, New York, 2015.Google Scholar
Grosswald, E., Die Werte der Riemannschen Zetafunktion an ungeraden Argumentstellen, Nachr. Akad. Wiss. Göttinger Math.-Phys. Kl. II (1970), 9–13.Google Scholar
Grosswald, E., Comments on some formulae of Ramanujan, Acta Arith. 21 (1972), 25–34.10.4064/aa-21-1-25-34Google Scholar
Grosswald, E., Relations between the values at integral arguments of Dirichlet series that satisfy functional equations, Proceedings of Symposia in Pure Mathematics 24, American Mathematical Society, Providence, 1973, 111–122.Google Scholar
Guinand, A. P., On Poisson’s summation formula, Ann. of Math. (2) 42 (1941), 591–603.10.2307/1969248Google Scholar
Gonek, S. M., Analytic Properties of zeta and $L$-functions, Thesis, University of Michigan, 1979.Google Scholar
Gun, S., Murty, M. R. and Rath, P., Transcendental values of certain Eichler integrals, Bull. Lond. Math. Soc. 43(5) (2011), 939–952.10.1112/blms/bdr031Google Scholar
Hančl, J. and Kristensen, S., Metrical irrationality results related to values of the Riemann $\unicode[STIX]{x1D701}$-function, preprint, February 12, 2018, arXiv:1802.03946v1.Google Scholar
Jahnke, E. and Emde, F., Tables of Fiunctions With Formulae and Curves, 4th ed. Dover Publications, New York, 1945.Google Scholar
Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M., On the values of the Riemann zeta-function at rational arguments, Hardy-Ramanujan J. 24 (2001), 11–19.Google Scholar
Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M., On rapidly convergent series for the Riemann zeta-values via the modular relation, Abh. Math. Semin. Univ. Hambg. 72 (2002), 187–206.10.1007/BF02941671Google Scholar
Kanemitsu, S., Tanigawa, Y. and Yoshimoto, M., On multiple Hurwitz zeta-function values at rational arguments, Acta Arith. 107(1) (2003), 45–67.10.4064/aa107-1-5Google Scholar
Kirschenhofer, P. and Prodinger, H., On some applications of formulae of Ramanujan in the analysis of algorithms, Mathematika 38(1) (1991), 14–33.10.1112/S0025579300006409Google Scholar
Koyama, S. and Kurokawa, N., Kummer’s formula for multiple gamma functions, J. Ramanujan Math. Soc. 18(1) (2003), 87–107.Google Scholar
Kummer, E. E., Beitrag zur Theorie der Function 𝛤(x) = ∫0∞e -vv x-1 dv, J. Reine Angew. Math. 35 (1847), 1–4.Google Scholar
Lagarias, J., Euler’s constant: Euler’s work and modern developments, Bull. Amer. Math. Soc. 50(4) (2013), 527–628.10.1090/S0273-0979-2013-01423-XGoogle Scholar
Lagrange, J., Une formule sommatoire et ses applications, Bull. Sci. Math. (2) 84 (1960), 105–110.Google Scholar
Lerch, M., Dalši studie v oboru Malmsténovských řad, Rozpravy České Akad. 3(28) (1894), 1–61.Google Scholar
Lerch, M., Sur la fonction 𝜁(s) pour valeurs impaires de l’argument, J. Sci. Math. Astron. pub. pelo Dr. F. Gomes Teixeira Coimbra 14 (1901), 65–69.Google Scholar
Luca, F. and Tachiya, Y., Linear independence of certain Lambert series, Proc. Amer. Math. Soc. 142(10) (2014), 3411–3419.10.1090/S0002-9939-2014-12102-2Google Scholar
Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and Theorems for the Special Functions of Mathematical Physics, 52, 3rd ed. Springer, New York, 1966.10.1007/978-3-662-11761-3Google Scholar
Masser, D., Rational values of the Riemann zeta function, J. Number Theory 131 (2011), 2037–2046.10.1016/j.jnt.2011.03.013Google Scholar
Murty, M. R., Smyth, C. and Wang, R. J., Zeros of Ramanujan polynomials, J. Ramanujan Math. Soc. 26(1) (2011), 107–125.Google Scholar
Oberhettinger, F., Tables of Mellin Transforms, Springer, New York, 1974.10.1007/978-3-642-65975-1Google Scholar
Olver, F. W. J., Error bounds for stationary phase approximations, SIAM J. Math. Anal. 5(1) (1974), 19–29.10.1137/0505003Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds), NIST Handbook of Mathematical Functions, Cambridge University Press, Cambridge, 2010.Google Scholar
Paris, R. B. and Kaminski, D., Asymptotics and Mellin-Barnes Integrals, Encyclopedia of Mathematics and its Applications 85, Cambridge University Press, Cambridge, 2001.10.1017/CBO9780511546662Google Scholar
Prudnikov, A. P., Brychkov, Yu. A. and Marichev, O. I., More Special Functions 3, Integrals and Series, Gordon and Breach, New York, 1986.Google Scholar
Rademacher, H., Trends in research: The Analytic Number Theory, Address delivered by invitation of the American Mathematical Society Program Committee, September 5, 1941; Bull. Amer. Math. Soc. 48 (1942), 379–401.10.1090/S0002-9904-1942-07679-8Google Scholar
Ramanujan, S., Notebooks (2 volumes), Tata Institute of Fundamental Research, Bombay, 1957; 2nd ed., 2012.Google Scholar
Ramanujan, S., The Lost Notebook and Other Unpublished Papers, Narosa, New Delhi, 1988.Google Scholar
Rivoal, T., La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs, C. R. Acad. Sci. Paris Sér. I Math. 331(4) (2000), 267–270.10.1016/S0764-4442(00)01624-4Google Scholar
Schlömilch, O., Ueber einige unendliche Reihen, Berichte über die Verh. d. Könige Sächsischen Gesell. Wiss. zu Leipzig 29 (1877), 101–105.Google Scholar
Spira, R., Zeros of Hurwitz zeta functions, Math. Comp. 30(136) (1976), 863–866.10.1090/S0025-5718-1976-0409382-2Google Scholar
Srivastava, H. M., Further series representations for 𝜁(2n + 1), Appl. Math. Comput. 97 (1998), 1–15.Google Scholar
Temme, N. M., Special Functions: An Introduction to the Classical Functions of Mathematical Physics, Wiley-Interscience Publication, New York, 1996.10.1002/9781118032572Google Scholar
Terras, A., Some formulas for the Riemann zeta function at odd integer argument resulting from Fourier expansions of the Epstein zeta function, Acta Arith. 29(2) (1976), 181–189.10.4064/aa-29-2-181-189Google Scholar
Terras, A., The Fourier expansion of Epstein’s zeta function over an algebraic number field and its consequences for algebraic number theory, Acta Arith. 32 (1977), 37–53.10.4064/aa-32-1-37-53Google Scholar
Titchmarsh, E. C., Theory of Fourier Integrals, 2nd ed. Clarendon Press, Oxford, 1948.Google Scholar
Voronin, S. M., On the zeros of zeta-functions of quadratic forms, Trudy Mat. Inst. Steklov 142 (1976), 135–147; English translation in Proc. Steklov Inst. Math. 3 (1979), 143–155.Google Scholar
Waldschmidt, M., Transcendence of periods: the state of the art, Pure Appl. Math. Q. 2(2) (2006), 435–463.10.4310/PAMQ.2006.v2.n2.a3Google Scholar
Wigert, S., Sur une extension de la série de Lambert, Arkiv Mat. Astron. Fys. 19 (1925), 13 pp.Google Scholar
Wilton, J. R., A proof of Burnside’s formula for log𝛤(x + 1) and certain allied properties of Riemann’s 𝜁-function, Mess. Math. 52 (1922/1923), 90–93.Google Scholar
Zudilin, W. W., One of the numbers 𝜁(5), 𝜁(7), 𝜁(9) and 𝜁(11) is irrational, Uspekhi Mat. Nauk 56(4) (2001), 149–150; translation in Russian Math. Surveys 56(4) (2001), 774–776.Google Scholar