Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-09T07:37:59.333Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTIONAL FOCK–SOBOLEV SPACES

Part of: Harmonic analysis in several variables Spaces and algebras of analytic functions Real functions Holomorphic functions of several complex variables

Published online by Cambridge University Press:  06 March 2018

HONG RAE CHO  and
SOOHYUN PARK
HONG RAE CHO
Affiliation:
Department of Mathematics, Pusan National University, Pusan 609-735, Republic of Korea email [email protected]
SOOHYUN PARK
Affiliation:
Department of Mathematics, Pusan National University, Pusan 609-735, Republic of Korea email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 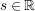$s\in \mathbb{R}$ and 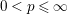$0<p\leqslant \infty$. The fractional Fock–Sobolev spaces 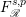$F_{\mathscr{R}}^{s,p}$ are introduced through the fractional radial derivatives 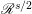$\mathscr{R}^{s/2}$. We describe explicitly the reproducing kernels for the fractional Fock–Sobolev spaces 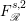$F_{\mathscr{R}}^{s,2}$ and then get the pointwise size estimate of the reproducing kernels. By using the estimate, we prove that the fractional Fock–Sobolev spaces 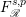$F_{\mathscr{R}}^{s,p}$ are identified with the weighted Fock spaces 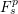$F_{s}^{p}$ that do not involve derivatives. So, the study on the Fock–Sobolev spaces is reduced to that on the weighted Fock spaces.

MSC classification

Primary: 30H20: Bergman spaces, Fock spaces 32A25: Integral representations; canonical kernels (Szegő, Bergman, etc.)
Secondary: 26A33: Fractional derivatives and integrals 42B35: Function spaces arising in harmonic analysis
Type
Article
Information
Nagoya Mathematical Journal , Volume 237 , March 2020 , pp. 79 - 97
Copyright
© 2018 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by NRF of Korea (NRF-2016R1D1A1B03933740).

References

Aronszajn, N., Theory of reproducing kernels , Trans. Amer. Math. Soc. 68(3) (1950), 337–404.Google Scholar
Bongioanni, B. and Torrea, J. L., Sobolev spaces associated to the harmonic oscillator , Proc. Indian Acad. Sci. Math. Sci. 116 (2006), 337–360.Google Scholar
Cho, H. R., Choe, B. R. and Koo, H., Linear combinations of composition operators on the Fock–Sobolev spaces , Potential Anal. 41 (2014), 1223–1246.Google Scholar
Cho, H. R., Choe, B. R. and Koo, H., Fock–Sobolev spaces of fractional order , Potential Anal. 43 (2015), 199–240.Google Scholar
Cho, H. R., Choi, H. and Lee, H.-W., Boundedness of the Segal–Bargmann Transform on Fractional Hermite–Sobolev Spaces , J. Funct. Spaces 2017 (2017), Article ID 9176914, 6 pages.Google Scholar
Cho, H. R. and Zhu, K., Fock–Sobolev spaces and their Carleson measures , J. Funct. Anal. 263(8) (2012), 2483–2506.Google Scholar
Choe, B. R. and Yang, J., Commutants of Toeplitz operators with radial symbols on the Fock–Sobolev space , J. Math. Anal. Appl. 415(2) (2014), 779–790.Google Scholar
Hall, B. and Lewkeeratiyutkul, W., Holomorphic Sobolev spaces and the generalised Segal–Bargmann transform , J. Funct. Anal. 217 (2004), 192–220.Google Scholar
Mengestie, T., Schatten class weighted composition operators on weighted Fock spaces , Arch. Math. (Basel) 101(4) (2013), 349–360.Google Scholar
Mengestie, T., Volterra type and weighted composition operators on weighted Fock spaces , Integral Equations Operator Theory 76(1) (2013), 81–94.Google Scholar
Mengestie, T., On trace ideal weighted composition operators on weighted Fock spaces , Arch. Math. (Basel) 105(5) (2015), 453–459.Google Scholar
Radha, R. and Thangavelu, S., Holomorphic Sobolev spaces, Hermite and special Hermite semigroups and a Paley–Wiener theorem for the windowed Fourier transform , J. Math. Anal. Appl. 354(2) (2009), 564–574.Google Scholar
Wang, X. F., Cao, G. F. and Xia, J., Toeplitz operators on Fock–Sobolev spaces with positive measure symbols , Sci. China Math. 57(7) (2014), 1443–1462.Google Scholar
Zhu, K. H., Operator Theory in Function Spaces, Monographs and Textbooks in Pure and Applied Mathematics 139 , Marcel Dekker, Inc., New York, 1990, xii+258 pp.Google Scholar
Zhu, K., Analysis on Fock spaces, Graduate Texts in Mathematics 263 , Springer, New York, 2012, x+344 pp.Google Scholar