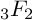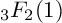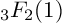Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Marta Na
and
Chu, Wenchang
2023.
Contiguous values for a class of nonterminating 3F2(1)-series.
Integral Transforms and Special Functions,
Vol. 34,
Issue. 6,
p.
457.
Chen, Marta Na
and
Chu, Wenchang
2024.
Bisection Series Approach for Exotic 3F2(1)-Series.
Mathematics,
Vol. 12,
Issue. 12,
p.
1915.
Chen, Marta Na
and
Chu, Wenchang
2024.
Yabu's formulae for hypergeometric $ _3F_2 $-series through Whipple's quadratic transformations.
AIMS Mathematics,
Vol. 9,
Issue. 8,
p.
21799.