Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T15:21:15.508Z Has data issue: false hasContentIssue false
  • English
  • Français

ENERGY CONCENTRATION PROPERTIES OF A p-GINZBURG–LANDAU MODEL

Part of: Equations of mathematical physics and other areas of application Variational problems in infinite-dimensional spaces Optimality conditions

Published online by Cambridge University Press:  25 August 2021

YUTIAN LEI Open the ORCID record for YUTIAN LEI [Opens in a new window]
YUTIAN LEI*
Affiliation:
Jiangsu Key Laboratory for NSLSCS School of Mathematical Sciences Nanjing Normal University Nanjing, 210023, China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the p-Ginzburg–Landau (p-GL) type model with 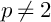$p\neq 2$ . First, we obtain global energy estimates and energy concentration properties by the singularity analysis. Next, we give a decay rate of 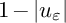$1-|u_\varepsilon |$ in the domain away from the singularities when 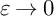$\varepsilon \to 0$ , where 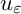$u_\varepsilon $ is a minimizer of p-GL functional with 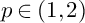$p \in (1,2)$ . Finally, we obtain a Liouville theorem for the finite energy solutions of the p-GL equation on 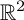$\mathbb {R}^2$ .

MSC classification

Primary: 35Q56: Ginzburg-Landau equations
Secondary: 49K20: Problems involving partial differential equations 58E20: Harmonic maps , etc.
Type
Article
Information
Nagoya Mathematical Journal , Volume 247 , September 2022 , pp. 494 - 515
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almog, Y., Berlyand, L., Golovaty, D., and Shafrir, I., Global minimizers for a $p$ -Ginzburg-Landau-type energy in ${\mathbb{R}}^2$ , J. Funct. Anal. 256 (2009), 2268–2290.CrossRefGoogle Scholar
Almog, Y., Berlyand, L., Golovaty, D., Shafrir, I., Radially symmetric minimizers for a p-Ginzburg-Landau type energy in ${\mathbb{R}}^2$ , Calc. Var. Partial Differ. Equat. 42 (2011), 517–546.Google Scholar
Bethuel, F., Brezis, H., Helein, F., Ginzburg-Landau Vortices, Birkhauser, Boston, 1994.Google Scholar
Brezis, H., Coron, J.-M., and Lieb, E., Harmonic maps with defects , Commun. Math. Phys., 107 (1986), 649–705.CrossRefGoogle Scholar
Brezis, H., Merle, F., and Riviere, T., Quantization effects for $-\Delta \mathrm{u}=u\left(1-{\left|u\right|}^2\right)$ in ${\mathbb{R}}^2$ , Arch. Rational Mech. Anal. 126 (1994), 35–58.CrossRefGoogle Scholar
Chen, Y., Hong, M., and Hungerbuhler, N., Heat flow of p-harmonic maps with values into spheres , Math. Z. 215 (1994), 25–35.CrossRefGoogle Scholar
Chong, T., Cheng, B., Dong, Y., and Zhang, W., Liouville theorems for critical points of the p-Ginzburg-Landau type functional, arXiv.1610.06301.Google Scholar
Comte, M. and Mironescu, P., Some properties of the Ginzburg-Landau minimizers , C. R. Acad. Sci. Paris 320 (1995), 1323–1326.Google Scholar
Comte, M. and Mironescu, P., The behavior of a Ginzburg-Landau minimizer near its zeros , Calc. Var. Partial Differ. Equat. 4 (1996), 323–340.CrossRefGoogle Scholar
Ding, S., Liu, Z., and Yu, W., A variational problem related to the Ginzburg-Landau model of superconductivity with normal impurity inclusion , SIAM J. Math. Anal. 29 (1998), 48–68.CrossRefGoogle Scholar
Giaquinta, M., Multiply Integrals in the Calculus of Variations and Nonlinear Elliptic Systems, Ann. Math. Stud., 105, Princeton University Press, Princeton, 1983.Google Scholar
Giaquinta, M. and Modica, G., Regularity results for some classes of higher order nonlinear elliptic systems , J. Reine Angew. Math. 311/312 (1979), 145–169.Google Scholar
Giaquinta, M. and Modica, G., Remarks on the regularity of the minimizers of certain degenerate functionals , Manus. Math. 57 (1986), 55–99.CrossRefGoogle Scholar
Hardt, R. and Lin, F., Singularities for $p$ -energy minimizing unit vector fields on planner domains , Calc. Var. Partial Differ. Equat. 3 (1995), 311–341.CrossRefGoogle Scholar
Hong, M., Asymptotic behavior for minimizers of a Ginzburg-Landau type functional in higher dimensions associated with n-harmonic maps , Adv. Differ. Equat. 1 (1996), 611–634.Google Scholar
Lei, Y., Asymptotic estimation for a p-Ginzburg-Landau type minimizer in higher dimensions , Pacific J. Math. 226 (2006), 103–135.CrossRefGoogle Scholar
Lei, Y., Asymptotic estimations for a p-Ginzburg-Landau type minimizer , Math. Nachr. 280 (2007), 1559–1576.CrossRefGoogle Scholar
Lei, Y., Singularity analysis of a p-Ginzburg-Landau type minimizer , Bull. Sci. Math. 134 (2010), 97–115.CrossRefGoogle Scholar
Lei, Y. and Xu, Y., Global analysis for a p-Ginzburg-Landau energy with radial structure, J. Math, Anal. Appl. 372 (2010), 538–548.CrossRefGoogle Scholar
Mironescu, P., Une estimation pour les minimiseurs de l’energie de Ginzburg-Landau , C. R. Acad. Sci. Paris 319 (1994), 941–943.Google Scholar
Struwe, M., On the asymptotic behaviour of minimizers of the Ginzburg-Landau model in 2 dimensions , Differ. Integral Equat. 7 (1994), 1613–1624.Google Scholar
Tolksdorf, P., Everywhere regularity for some quasilinear systems with a lack of ellipticity , Ann. Math. Pura. Appl. 134 (1983), 241–266.CrossRefGoogle Scholar
Uhlenbeck, K., Regularity for a class of nonlinear elliptic systems , Acta Math. 138 (1977), 219–240.CrossRefGoogle Scholar
Wang, C., Limits of solutions to the generalized Ginzburg-Landau functional , Comm. Partial Differ. Equat. 27 (2002), 877–906.Google Scholar