Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T23:15:04.908Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONJECTURE ON 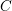$C$-MATRICES OF CLUSTER ALGEBRAS

Part of: Algebraic combinatorics Arithmetic rings and other special rings

Published online by Cambridge University Press:  19 June 2018

PEIGEN CAO ,
MIN HUANG  and
FANG LI
PEIGEN CAO
Affiliation:
School of Mathematical Sciences, Zhejiang University (Yuquan Campus), Hangzhou, Zhejiang 310027, PR China email [email protected]
MIN HUANG
Affiliation:
Département de mathématiques, Université de Sherbrooke, Sherbrooke, Québec, J1K 2R1, Canada email [email protected]
FANG LI*
Affiliation:
School of Mathematical Sciences, Zhejiang University (Yuquan Campus), Hangzhou, Zhejiang 310027, PR China email [email protected]
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

For a skew-symmetrizable cluster algebra 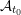${\mathcal{A}}_{t_{0}}$ with principal coefficients at 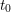$t_{0}$, we prove that each seed 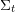$\unicode[STIX]{x1D6F4}_{t}$ of 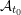${\mathcal{A}}_{t_{0}}$ is uniquely determined by its 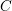$C$-matrix, which was proposed by Fomin and Zelevinsky (Compos. Math. 143 (2007), 112–164) as a conjecture. 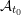Our proof is based on the fact that the positivity of cluster variables and sign coherence of $c$-vectors hold for ${\mathcal{A}}_{t_{0}}$, which was actually verified in Gross et al. (Canonical bases for cluster algebras, J. Amer. Math. Soc. 31(2) (2018), 497–608). Further discussion is provided in the sign-skew-symmetric case so as to obtain a weak version of the conjecture in this general case.

MSC classification

Primary: 13F60: Cluster algebras 05E40: Combinatorial aspects of commutative algebra
Type
Article
Information
Nagoya Mathematical Journal , Volume 238 , June 2020 , pp. 37 - 46
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cao, P. G. and Li, F., Some conjectures on generalized cluster algebras via the cluster formula and D-matrix pattern, J. Algebra 493 (2018), 57–78.Google Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: applications to cluster algebras, J. Amer. Math. Soc. 23(3) (2010), 749–790.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations, J. Amer. Math. Soc. 15(2) (2002), 497–529 (electronic).Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. IV. Coefficients, Compos. Math. 143 (2007), 112–164.Google Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., Canonical bases for cluster algebras, J. Amer. Math. Soc. 31(2) (2018), 497–608.Google Scholar
Huang, M. and Li, F., Unfolding of acyclic sign-skew-symmetric cluster algebras and applications to positivity and F-polynomials, submitted, arXiv:1609.05981v2.Google Scholar
Inoue, R., Iyama, O., Keller, B., Kuniba, A. and Nakanishi, T., Periodicities of T and Y-systems, dilogarithm identities, and cluster algebras I: type B r, Publ. Res. Inst. Math. Sci. 49 (2013), 1–42; arXiv:1001.1880, 35 pp.Google Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras, Ann. of Math. 182 (2015), 73–125.Google Scholar
Marsh, R. J., Lecture Notes on Cluster Algebras, Zurich Lectures in Advanced Mathematics, European Mathematical Society Publishing House, Zürich, 2013.Google Scholar
Nakanishi, T., Structure of seeds in generalized cluster algebras, Pacific J. Math. 277(1) (2015), 201–218.Google Scholar
Nakanishi, T. and Zelevinsky, A., “On tropical dualities in cluster algebras”, in Algebraic Groups and Quantum Groups, Contemporary Mathematics 565, American Mathematical Society, Providence, RI, 2012, 217–226.Google Scholar
Plamondon, P.-G., Cluster algebras via cluster categories with infinite-dimensional morphism spaces, Compos. Math. 147(6) (2011), 1921–1954.Google Scholar
Plamondon, P.-G., Cluster characters for cluster categories with infinite-dimensional morphism spaces, Adv. Math. 227(1) (2011), 1–39.Google Scholar
Reading, N. and Speyer, D. E., Combinatorial frameworks for cluster algebras, Int. Math. Res. Not. 2016(1) (2016), 109–173.Google Scholar