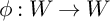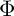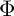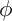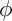1 Introduction
1.1 Introduction
Let
![]() $ W $
be a Weinstein manifold equipped with a compactly supported, exact symplectic automorphism
$ W $
be a Weinstein manifold equipped with a compactly supported, exact symplectic automorphism
![]() $ \phi $
. The pair
$ \phi $
. The pair
![]() $ (W, \phi ) $
forms a discrete dynamical system. In this paper, we compare two invariants of this dynamical system.
$ (W, \phi ) $
forms a discrete dynamical system. In this paper, we compare two invariants of this dynamical system.
The first invariant is the topological entropy. This concept was introduced in the 1960s for compact spaces and extended to noncompact spaces in the 1970s. See [Reference Adler, Konheim and McAndrew2], [Reference Hofer32], [Reference Hofer33]. For readers unfamiliar with dynamical systems, the books [Reference Brin and Stuck12], [Reference Katok and Hasselblatt34], [Reference Robinson44] are excellent references. Let
![]() $ h_{top}(\phi ) $
denote the classical invariant associated with
$ h_{top}(\phi ) $
denote the classical invariant associated with
![]() $ (W, \phi ) $
.
$ (W, \phi ) $
.
Recently, [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18] introduced the concept of categorical entropy for a pair
![]() $ (\mathcal {C}, \Phi ) $
, where
$ (\mathcal {C}, \Phi ) $
, where
![]() $ \mathcal {C} $
is a triangulated category and
$ \mathcal {C} $
is a triangulated category and
![]() $ \Phi : \mathcal {C} \to \mathcal {C} $
is an auto-equivalence. In our setting, the dynamical system
$ \Phi : \mathcal {C} \to \mathcal {C} $
is an auto-equivalence. In our setting, the dynamical system
![]() $ (W, \phi ) $
induces a categorical dynamical system
$ (W, \phi ) $
induces a categorical dynamical system
![]() $ (\mathcal {C}, \Phi ) $
of symplectic-topological nature. Specifically,
$ (\mathcal {C}, \Phi ) $
of symplectic-topological nature. Specifically,
-
• the (triangulated closure of the) wrapped Fukaya category
 $ \mathcal {W}(W) $
of a Weinstein manifold
$ \mathcal {W}(W) $
of a Weinstein manifold
 $ W $
is a triangulated category, and
$ W $
is a triangulated category, and -
• the exact symplectic automorphism
 $ \phi $
induces an auto-equivalence
$ \phi $
induces an auto-equivalence
 $ \Phi : \mathcal {W}(W) \to \mathcal {W}(W) $
.
$ \Phi : \mathcal {W}(W) \to \mathcal {W}(W) $
.
This construction gives rise to the second invariant of the symplectic dynamical system
![]() $ (W, \phi ) $
: the categorical entropy of
$ (W, \phi ) $
: the categorical entropy of
![]() $ (\mathcal {W}(W), \Phi ) $
. Let
$ (\mathcal {W}(W), \Phi ) $
. Let
![]() $ h_{cat}(\phi ) $
denote this invariant, which we refer to as the categorical entropy of
$ h_{cat}(\phi ) $
denote this invariant, which we refer to as the categorical entropy of
![]() $ \phi $
.
$ \phi $
.
Since both entropies are invariants of the same dynamical system, it is natural to compare them. In this paper, we establish the inequality:
Remark 1.1.
-
1. [Reference Kikuta and Ouchi35], [Reference Mattei38] studied the comparison of these two entropies in an algebro-geometric setting. In particular, [Reference Kikuta and Ouchi35] considered a pair
 $ (X, \phi ) $
, where
$ (X, \phi ) $
, where
 $ X $
is a smooth projective variety, and
$ X $
is a smooth projective variety, and
 $ \phi $
is a surjective endomorphism of
$ \phi $
is a surjective endomorphism of
 $ X $
. Here,
$ X $
. Here,
 $ \phi $
induces an auto-equivalence
$ \phi $
induces an auto-equivalence
 $ \Phi $
on the derived category of coherent sheaves. The induced categorical dynamical system defines the categorical entropy of
$ \Phi $
on the derived category of coherent sheaves. The induced categorical dynamical system defines the categorical entropy of
 $ \phi $
. In this context, [Reference Kikuta and Ouchi35] proved the equality
$ \phi $
. In this context, [Reference Kikuta and Ouchi35] proved the equality
 $ h_{cat}(\Phi ) = h_{top}(\phi ) $
.
$ h_{cat}(\Phi ) = h_{top}(\phi ) $
. -
2. In the symplectic-geometric setting, [Reference Bae, Choa, Jeong, Karabas and Lee9] proved the inequality
 $ h_{cat}(\phi ) \leq h_{top}(\phi ) $
in specific cases.
$ h_{cat}(\phi ) \leq h_{top}(\phi ) $
in specific cases.
Before presenting formal statements of our results, we provide additional context, particularly references that explore the relationship between symplectic-topological invariants and the topological entropy of symplectic dynamical systems. The symplectic-topological invariants we focus on here are Floer-theoretic invariants, as Lagrangian Floer theory plays a key role in connecting categorical and topological entropy in this work. However, there are numerous other significant results in the study of symplectic dynamical systems; see, for example, [Reference Alves3]–[Reference Alves and Meiwes5], [Reference Dahinden16], [Reference Dahinden17], [Reference Smith46].
Floer theory produces various chain complexes and their homologies from symplectic manifolds and associated data. For instance, given a symplectic manifold
![]() $ X $
and a symplectic automorphism
$ X $
and a symplectic automorphism
![]() $ \phi : X \to X $
, one can define the fixed-point Floer homology
$ \phi : X \to X $
, one can define the fixed-point Floer homology
![]() $ HF_*(\phi ^n) $
for each
$ HF_*(\phi ^n) $
for each
![]() $ n \in \mathbb {Z} $
. When
$ n \in \mathbb {Z} $
. When
![]() $ X $
is a compact surface and
$ X $
is a compact surface and
![]() $ \phi $
is a symplectomorphism of
$ \phi $
is a symplectomorphism of
![]() $ X $
, Fel’shtyn [Reference Fel’shtyn23] related the topological entropy of
$ X $
, Fel’shtyn [Reference Fel’shtyn23] related the topological entropy of
![]() $ \phi $
to the growth rate of
$ \phi $
to the growth rate of
![]() $ \dim HF_*(\phi ^n) $
as
$ \dim HF_*(\phi ^n) $
as
![]() $ n \to \infty $
. Similarly, Frauenfelder and Schlenk [Reference Frauenfelder and Schlenk25], [Reference Frauenfelder and Schlenk26], as well as Macarini and Schlenk [Reference Macarini and Schlenk39], observed a connection between the growth rate of dimensions of Lagrangian Floer homology and the topological entropy of the corresponding dynamical system.
$ n \to \infty $
. Similarly, Frauenfelder and Schlenk [Reference Frauenfelder and Schlenk25], [Reference Frauenfelder and Schlenk26], as well as Macarini and Schlenk [Reference Macarini and Schlenk39], observed a connection between the growth rate of dimensions of Lagrangian Floer homology and the topological entropy of the corresponding dynamical system.
In contact topology, a mathematical cousin of symplectic topology, it is known that the topological entropy of Reeb flows is bounded below by the exponential growth rate of the dimension of contact homology. For related results, see [Reference Alves, Colin and Honda1].
We note that the results cited above primarily relate the topological entropy to the dimensions of Floer homology. More recently, leveraging ideas from topological data analysis and the theory of persistence modules, researchers have begun to study the relationship between the topological entropy of symplectic dynamical systems and the dimensions of Floer chain complexes. For example, Cineli, Ginzburg, Gürel [Reference Cineli, Ginzburg and Gürel13] explored the entropy of Hamiltonian flows using these methods.
In this paper, when
![]() $ W $
is a Weinstein manifold and
$ W $
is a Weinstein manifold and
![]() $ \phi $
is a compactly supported symplectic automorphism, we relate the categorical entropy of
$ \phi $
is a compactly supported symplectic automorphism, we relate the categorical entropy of
![]() $ \phi $
to the growth of dimensions of Lagrangian Floer homologies and the topological entropy of
$ \phi $
to the growth of dimensions of Lagrangian Floer homologies and the topological entropy of
![]() $ \phi $
to the growth of dimensions of Lagrangian Floer cochain complexes. Detailed statements of our results and an outline of the methods will be presented in the next subsection.
$ \phi $
to the growth of dimensions of Lagrangian Floer cochain complexes. Detailed statements of our results and an outline of the methods will be presented in the next subsection.
1.2 Results
One of our main results is the inequality given in (1.1). A key reason why we have an inequality instead of an equality in (1.1) is that
![]() $h_{cat}(\phi )$
is invariant under compactly supported Hamiltonian isotopy, whereas
$h_{cat}(\phi )$
is invariant under compactly supported Hamiltonian isotopy, whereas
![]() $h_{top}(\phi )$
is not. In other words, if
$h_{top}(\phi )$
is not. In other words, if
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
are Hamiltonian isotopic, then
$\phi _2$
are Hamiltonian isotopic, then
![]() $h_{cat}(\phi _1) = h_{cat}(\phi _2)$
. This is because
$h_{cat}(\phi _1) = h_{cat}(\phi _2)$
. This is because
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
induce the same auto-equivalence on
$\phi _2$
induce the same auto-equivalence on
![]() $\mathcal {W}(W)$
. However,
$\mathcal {W}(W)$
. However,
![]() $h_{top}(\phi _1)$
and
$h_{top}(\phi _1)$
and
![]() $h_{top}(\phi _2)$
do not necessarily coincide. Thus, one might expect the topological entropy to be more sensitive than the categorical entropy, making the inequality in Theorem 1.2 plausible.
$h_{top}(\phi _2)$
do not necessarily coincide. Thus, one might expect the topological entropy to be more sensitive than the categorical entropy, making the inequality in Theorem 1.2 plausible.
Theorem 1.2 (=Theorem 4.1).
The categorical entropy of
![]() $\phi $
bounds the topological entropy of
$\phi $
bounds the topological entropy of
![]() $\phi $
from below, that is,
$\phi $
from below, that is,
Sketch of Proof
Let
![]() $\mathcal {C}$
be a triangulated category with a generator G, and let
$\mathcal {C}$
be a triangulated category with a generator G, and let
![]() $\Phi : \mathcal {C} \to \mathcal {C}$
be an auto-equivalence. By [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6], if
$\Phi : \mathcal {C} \to \mathcal {C}$
be an auto-equivalence. By [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6], if
![]() $\mathcal {C}$
is smooth and proper, then
$\mathcal {C}$
is smooth and proper, then
For the given dynamical system
![]() $(W, \phi )$
, we note that the wrapped Fukaya category
$(W, \phi )$
, we note that the wrapped Fukaya category
![]() $\mathcal {W}(W)$
of W is smooth but not necessarily proper. Thus, [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6] cannot be applied directly.
$\mathcal {W}(W)$
of W is smooth but not necessarily proper. Thus, [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6] cannot be applied directly.
However, a fully stopped partially wrapped Fukaya category is proper. Moreover, by Lemma 2.10, the categorical entropies of
![]() $\phi $
on
$\phi $
on
![]() $\mathcal {W}(W)$
and on a partially wrapped Fukaya category are the same. Thus, Equation (1.2) holds if
$\mathcal {W}(W)$
and on a partially wrapped Fukaya category are the same. Thus, Equation (1.2) holds if
![]() $\operatorname {Hom}$
refers to the morphism space in a fully stopped partially wrapped Fukaya category.
$\operatorname {Hom}$
refers to the morphism space in a fully stopped partially wrapped Fukaya category.
To complete the proof, we show that the right-hand side of Equation (1.2) bounds
![]() $h_{top}(\phi )$
from below. The key idea is to apply Crofton’s inequality (3.3), introduced in Lemma 3.4. (Note that the inequality in (3.3) is a modification of [Reference Cineli, Ginzburg and Gürel13, Lemma 5.3]. For additional context, see Remark 3.5.)
$h_{top}(\phi )$
from below. The key idea is to apply Crofton’s inequality (3.3), introduced in Lemma 3.4. (Note that the inequality in (3.3) is a modification of [Reference Cineli, Ginzburg and Gürel13, Lemma 5.3]. For additional context, see Remark 3.5.)
Specifically, let
![]() $L_1 = G$
and
$L_1 = G$
and
![]() $L_2 = \phi ^n(G)$
, where G is a generator of a partially wrapped Fukaya category and
$L_2 = \phi ^n(G)$
, where G is a generator of a partially wrapped Fukaya category and
![]() $n \in \mathbb {Z}_{\geq 1}$
. Then, combining (1.2) and (4.2), we conclude that the exponential growth of the left-hand side of (3.3) bounds the categorical entropy of
$n \in \mathbb {Z}_{\geq 1}$
. Then, combining (1.2) and (4.2), we conclude that the exponential growth of the left-hand side of (3.3) bounds the categorical entropy of
![]() $\phi $
from above, while the exponential growth of the right-hand side bounds the topological entropy of
$\phi $
from above, while the exponential growth of the right-hand side bounds the topological entropy of
![]() $\phi $
from below. See Lemma 3.4 and Section 4 for details.
$\phi $
from below. See Lemma 3.4 and Section 4 for details.
For the categorical entropy of
![]() $\phi $
, we primarily work with the wrapped Fukaya category
$\phi $
, we primarily work with the wrapped Fukaya category
![]() $\mathcal {W}(W)$
. However, there exists another triangulated category associated with W: the compact Fukaya category
$\mathcal {W}(W)$
. However, there exists another triangulated category associated with W: the compact Fukaya category
![]() $\mathcal {F}(W)$
(or its triangulated closure). This raises the question: why do we choose
$\mathcal {F}(W)$
(or its triangulated closure). This raises the question: why do we choose
![]() $\mathcal {W}(W)$
over
$\mathcal {W}(W)$
over
![]() $\mathcal {F}(W)$
?
$\mathcal {F}(W)$
?
The reasons are as follows:
-
• It is well-known that
 $\mathcal {W}(W)$
admits a Lagrangian generator. For
$\mathcal {W}(W)$
admits a Lagrangian generator. For
 $\mathcal {F}(W)$
, the existence of a Lagrangian generator is not known in general for arbitrary W.
$\mathcal {F}(W)$
, the existence of a Lagrangian generator is not known in general for arbitrary W. -
•
 $\mathcal {W}(W)$
is a smooth category, while
$\mathcal {W}(W)$
is a smooth category, while
 $\mathcal {F}(W)$
is not necessarily smooth. Thus, [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6] cannot be applied to
$\mathcal {F}(W)$
is not necessarily smooth. Thus, [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6] cannot be applied to
 $\mathcal {F}(W)$
.
$\mathcal {F}(W)$
.
Nevertheless, if assumptions are added to resolve these issues, one could expect inequality (1.1) to hold for
![]() $\mathcal {F}(W)$
as well. With this perspective, we prove Theorem 1.3.
$\mathcal {F}(W)$
as well. With this perspective, we prove Theorem 1.3.
Theorem 1.3 (=Theorem 6.3).
Let
![]() $(W, \phi : W \to W)$
satisfy the hypotheses in Lemma 6.2. Let
$(W, \phi : W \to W)$
satisfy the hypotheses in Lemma 6.2. Let
![]() $\Phi _{\mathcal {F}(W)}$
denote the functor induced by
$\Phi _{\mathcal {F}(W)}$
denote the functor induced by
![]() $\phi $
on the compact Fukaya category
$\phi $
on the compact Fukaya category
![]() $\mathcal {F}(W)$
. Then the categorical entropy
$\mathcal {F}(W)$
. Then the categorical entropy
![]() $h_{cat}(\Phi _{\mathcal {F}(W)})$
bounds the topological entropy of
$h_{cat}(\Phi _{\mathcal {F}(W)})$
bounds the topological entropy of
![]() $\phi $
from below:
$\phi $
from below:
1.3 Further questions
At the beginning of Section 1.2, we highlighted a reason why we expect the inequality (1.1): categorical entropy cannot distinguish members of a Hamiltonian isotopic class, whereas topological entropy can. Here, we present another philosophical reason for this expectation.
To explain this reason, we review a property of topological entropy. By [Reference Newhouse40], [Reference Przytycki43], [Reference Yomdin50], it is known that
 $$\begin{align*} & h_{top}(\phi) \\ &= \sup_{\text{compact submanifold } Y \subset W} \left(\text{the exponential growth rate of } \mathrm{Vol}\left(\phi^n(Y)\right) \text{ with respect to } n\right). \end{align*}$$
$$\begin{align*} & h_{top}(\phi) \\ &= \sup_{\text{compact submanifold } Y \subset W} \left(\text{the exponential growth rate of } \mathrm{Vol}\left(\phi^n(Y)\right) \text{ with respect to } n\right). \end{align*}$$
In other words,
![]() $h_{top}(\phi )$
can be computed by taking the supremum over all submanifolds Y.
$h_{top}(\phi )$
can be computed by taking the supremum over all submanifolds Y.
On the other hand, the categorical entropy of
![]() $\phi $
is only influenced by exact Lagrangian submanifolds; other submanifolds do not contribute to the categorical entropy.
$\phi $
is only influenced by exact Lagrangian submanifolds; other submanifolds do not contribute to the categorical entropy.
As a counterpart to the exponential growth rate of
![]() $\mathrm {Vol}\left (\phi ^n(Y)\right )$
, we define another entropy, called barcode entropy. This notion is a slight modification of the relative barcode entropy introduced in [Reference Cineli, Ginzburg and Gürel13]. By definition, barcode entropy is not an invariant of the dynamical system
$\mathrm {Vol}\left (\phi ^n(Y)\right )$
, we define another entropy, called barcode entropy. This notion is a slight modification of the relative barcode entropy introduced in [Reference Cineli, Ginzburg and Gürel13]. By definition, barcode entropy is not an invariant of the dynamical system
![]() $(W, \phi )$
but rather an invariant of
$(W, \phi )$
but rather an invariant of
![]() $(W, \phi , L_1, L_2)$
, where
$(W, \phi , L_1, L_2)$
, where
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are Lagrangian submanifolds of W. We denote the barcode entropy for
$L_2$
are Lagrangian submanifolds of W. We denote the barcode entropy for
![]() $(W, \phi , L_1, L_2)$
by
$(W, \phi , L_1, L_2)$
by
![]() $h_{bar}(\phi; L_1, L_2)$
. For details, see Section 7.
$h_{bar}(\phi; L_1, L_2)$
. For details, see Section 7.
With this definition, we establish Proposition 1.4.
Proposition 1.4 (=Propositions 7.6 and 7.7).
For a pair of Lagrangians
![]() $(L_1, L_2)$
satisfying the conditions in Section 7,
$(L_1, L_2)$
satisfying the conditions in Section 7,
Based on Proposition 1.4 and the preceding discussion, we ask whether the following equations hold:
 $$ \begin{align*} & h_{cat}(\phi) = \inf_{L_1, L_2} h_{bar}(\phi; L_1, L_2),\\ & h_{top}(\phi) = \sup_{L_1, L_2} h_{bar}(\phi; L_1, L_2). \end{align*} $$
$$ \begin{align*} & h_{cat}(\phi) = \inf_{L_1, L_2} h_{bar}(\phi; L_1, L_2),\\ & h_{top}(\phi) = \sup_{L_1, L_2} h_{bar}(\phi; L_1, L_2). \end{align*} $$
1.4 Structure of the paper
The paper consists of six sections except Section 1. Section 2 reviews definitions and preliminaries. Sections 3 and 4 prove the main theorem, that is, Theorem 1.2. Section 5 discusses two examples: the first example shows that the inequality (1.1) can be strict, and the second example shows that categorical entropy could force topological entropy to be positive. Section 6 considers the compact Fukaya category of W under some assumptions. Section 7 is about the further questions described in Section 1.3.
2 Preliminaries
In this section, we give some preliminaries on Lagrangian Floer theory and (partially) wrapped Fukaya categories. Then we also introduce the notions of topological entropy and categorical entropy.
2.1 Lagrangian Floer theory
Let
![]() $\hat {W}$
be a Weinstein manifold with a Liouville one form
$\hat {W}$
be a Weinstein manifold with a Liouville one form
![]() $\lambda $
, which means that
$\lambda $
, which means that
![]() $(\hat {W},\omega =d\lambda )$
is a non-compact symplectic manifold such that the Liouville vector field Z, that is, Z is a vector field on
$(\hat {W},\omega =d\lambda )$
is a non-compact symplectic manifold such that the Liouville vector field Z, that is, Z is a vector field on
![]() $\hat {W}$
characterized by
$\hat {W}$
characterized by
![]() $\iota _Z \omega = \lambda $
, is gradient-like with respect to a certain Morse function on
$\iota _Z \omega = \lambda $
, is gradient-like with respect to a certain Morse function on
![]() $\hat {W}$
. See [Reference Cieliebak and Eliashberg15] for a reference on Weinstein manifolds. Then, there exists a Weinstein domain W whose completion is
$\hat {W}$
. See [Reference Cieliebak and Eliashberg15] for a reference on Weinstein manifolds. Then, there exists a Weinstein domain W whose completion is
![]() $\hat {W}$
. In other words,
$\hat {W}$
. In other words,
![]() $(W, \omega |_{W}=d\lambda |_{W})$
is a compact symplectic submanifold with boundary of
$(W, \omega |_{W}=d\lambda |_{W})$
is a compact symplectic submanifold with boundary of
![]() $\hat {W}$
of codimension
$\hat {W}$
of codimension
![]() $0$
, for which the Liouville vector field points outward along the boundary
$0$
, for which the Liouville vector field points outward along the boundary
![]() $\partial W$
, and
$\partial W$
, and
![]() $\hat {W}$
is obtained from W by gluing the cylindrical end
$\hat {W}$
is obtained from W by gluing the cylindrical end
![]() $[1,\infty ) \times \partial W$
along
$[1,\infty ) \times \partial W$
along
![]() $\partial W$
, namely,
$\partial W$
, namely,
Furthermore, on the cylindrical end
![]() $[1,\infty ) \times \partial W$
, the Liouville one form
$[1,\infty ) \times \partial W$
, the Liouville one form
![]() $\lambda $
satisfies
$\lambda $
satisfies
where r is the coordinate for
![]() $[1,\infty )$
and
$[1,\infty )$
and
![]() $\alpha := \lambda |_{\partial W}$
. We remark that
$\alpha := \lambda |_{\partial W}$
. We remark that
![]() $\partial W$
is a contact manifold with the contact form
$\partial W$
is a contact manifold with the contact form
![]() $\alpha $
. Furthermore, since the Liouville vector field Z does not vanish outside a compact subset of
$\alpha $
. Furthermore, since the Liouville vector field Z does not vanish outside a compact subset of
![]() $\hat {W}$
, we may consider the orbit space
$\hat {W}$
, we may consider the orbit space
![]() $\partial _\infty \hat {W}$
of the flow of Z at infinity, which we will call the ideal boundary of
$\partial _\infty \hat {W}$
of the flow of Z at infinity, which we will call the ideal boundary of
![]() $\hat {W}$
. One can deduce that
$\hat {W}$
. One can deduce that
![]() $\partial W$
is naturally diffeomorphic to
$\partial W$
is naturally diffeomorphic to
![]() $\partial _\infty \hat {W}$
.
$\partial _\infty \hat {W}$
.
Remark 2.1. We would like to point out that for a given Weinstein manifold
![]() $\hat {W}$
, the choice of a Weinstein domain W is not unique. It seems that the choice of W is related to the construction of wrapped Fukaya category of
$\hat {W}$
, the choice of a Weinstein domain W is not unique. It seems that the choice of W is related to the construction of wrapped Fukaya category of
![]() $\hat {W}$
. For example, the notion of cylindrical at
$\hat {W}$
. For example, the notion of cylindrical at
![]() $\infty $
depends on the choice of W, see Definition 2.2. However, it is well-known that the choice of W does not change the Morita-equivalence class of the resulting wrapped Fukaya category of
$\infty $
depends on the choice of W, see Definition 2.2. However, it is well-known that the choice of W does not change the Morita-equivalence class of the resulting wrapped Fukaya category of
![]() $\hat {W}$
. In the current paper, in order to avoid unnecessarily confusion, we assume that a Weinstein domain W is given and
$\hat {W}$
. In the current paper, in order to avoid unnecessarily confusion, we assume that a Weinstein domain W is given and
![]() $\hat {W}$
is defined to be the completion of W.
$\hat {W}$
is defined to be the completion of W.
To discuss the Floer theory of a pair of Lagrangian submanifolds of
![]() $\hat {W}$
, let J be an almost complex structure on
$\hat {W}$
, let J be an almost complex structure on
![]() $\hat {W}$
that is compatible with the symplectic form
$\hat {W}$
that is compatible with the symplectic form
![]() $\omega = d \lambda $
and is of contact type at
$\omega = d \lambda $
and is of contact type at
![]() $\infty $
. The first condition means that the symplectic structure
$\infty $
. The first condition means that the symplectic structure
![]() $\omega $
and the almost complex structure J determine a Riemannian metric g on W given by
$\omega $
and the almost complex structure J determine a Riemannian metric g on W given by
The latter condition means that the almost complex structure J maps the Liouville vector field Z to the Reeb vector field associated with
![]() $\alpha $
on
$\alpha $
on
![]() $\partial W$
and preserves the contact distribution, which is necessary to apply maximum principles to J-holomorphic curves in
$\partial W$
and preserves the contact distribution, which is necessary to apply maximum principles to J-holomorphic curves in
![]() $\hat {W}$
.
$\hat {W}$
.
Definition 2.2. An exact Lagrangian submanifold L of
![]() $(\hat {W},\omega )$
is cylindrical (at
$(\hat {W},\omega )$
is cylindrical (at
![]() $\infty $
) if L and
$\infty $
) if L and
![]() $\partial W$
intersect transversely and
$\partial W$
intersect transversely and
where
![]() $\mathcal {L} := L \cap \partial W$
.
$\mathcal {L} := L \cap \partial W$
.
For convenience, we will use the term “Lagrangian” instead of “exact Lagrangian submanifold that is cylindrical at
![]() $\infty $
”.
$\infty $
”.
Let us assume that
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are a transversal pair of Lagrangians in
$L_2$
are a transversal pair of Lagrangians in
![]() $\hat {W}$
. Since
$\hat {W}$
. Since
![]() $L_i$
is an exact Lagrangian submanifold, there is a primitive function
$L_i$
is an exact Lagrangian submanifold, there is a primitive function
such that
![]() $\lambda |_{L_i} = d f_i$
. Let us fix such a primitive function
$\lambda |_{L_i} = d f_i$
. Let us fix such a primitive function
![]() $h_i$
for each Lagrangian
$h_i$
for each Lagrangian
![]() $L_i$
.
$L_i$
.
Let
![]() $\mathcal {P}(L_1, L_2)$
be the space of paths from
$\mathcal {P}(L_1, L_2)$
be the space of paths from
![]() $L_1$
to
$L_1$
to
![]() $L_2$
in
$L_2$
in
![]() $\hat {W}$
. We define the action functional
$\hat {W}$
. We define the action functional
by
 $$\begin{align*}\mathcal{A}(\gamma) := -\int \gamma^*\lambda - h_1(\gamma(0)) + h_2(\gamma(1)), \forall \gamma \in \mathcal{P}(L_1,L_2).\end{align*}$$
$$\begin{align*}\mathcal{A}(\gamma) := -\int \gamma^*\lambda - h_1(\gamma(0)) + h_2(\gamma(1)), \forall \gamma \in \mathcal{P}(L_1,L_2).\end{align*}$$
Let us further equip the path space
![]() $\mathcal {P}(L_1,L_2)$
with the standard
$\mathcal {P}(L_1,L_2)$
with the standard
![]() $L^2$
-metric induced by g. Then it is straightforward to check that
$L^2$
-metric induced by g. Then it is straightforward to check that
-
• critical points of the action functional
 $\mathcal {A}$
are constant paths from
$\mathcal {A}$
are constant paths from
 $L_1$
to
$L_1$
to
 $L_2$
, that is, intersection points of
$L_2$
, that is, intersection points of
 $L_1$
and
$L_1$
and
 $L_2$
, and
$L_2$
, and -
• gradient flows are given by strips
satisfying $$\begin{align*}u : \mathbb{R} \times [0,1] \to \hat{W}\end{align*}$$
and the J-holomorphic equation
$$\begin{align*}u : \mathbb{R} \times [0,1] \to \hat{W}\end{align*}$$
and the J-holomorphic equation $$\begin{align*}u(s,0) \in L_1, u(s,1)\in L_2, \forall s\in \mathbb{R}\end{align*}$$
$$\begin{align*}u(s,0) \in L_1, u(s,1)\in L_2, \forall s\in \mathbb{R}\end{align*}$$
 $$ \begin{align*} \partial_s u+ J \partial_t u =0& , \forall (s,t) \in \mathbb{R} \times [0,1]. \end{align*} $$
$$ \begin{align*} \partial_s u+ J \partial_t u =0& , \forall (s,t) \in \mathbb{R} \times [0,1]. \end{align*} $$
The Lagrangian Floer complex
![]() $CF^*(L_1,L_2)$
is given by the Morse complex for the action functional
$CF^*(L_1,L_2)$
is given by the Morse complex for the action functional
![]() $\mathcal {A} =\mathcal {A}_{L_1,L_2}$
. Indeed, for a given field k,
$\mathcal {A} =\mathcal {A}_{L_1,L_2}$
. Indeed, for a given field k,
-
•
 $CF^*(L_1,L_2)$
is a graded k-vector space generated by intersection points
$CF^*(L_1,L_2)$
is a graded k-vector space generated by intersection points
 $L_1 \cap L_2$
, and
$L_1 \cap L_2$
, and -
• the differential
 $\delta : CF^*(L_1,L_2) \to CF^{*+1} (L_1,L_2)$
is defined by counting J-holomorphic strips of index
$\delta : CF^*(L_1,L_2) \to CF^{*+1} (L_1,L_2)$
is defined by counting J-holomorphic strips of index
 $1$
between two intersection points of
$1$
between two intersection points of
 $L_1$
and
$L_1$
and
 $L_2$
.
$L_2$
.
We call the resulting cohomology Lagrangian Floer cohomology between
![]() $L_1$
and
$L_1$
and
![]() $L_2$
and denote it by
$L_2$
and denote it by
![]() $HF^*(L_1,L_2)$
.
$HF^*(L_1,L_2)$
.
We would like to point out that the grading of the Floer cochain complex is not crucial in our remaining arguments. We will just assume that one of the followings holds.
-
• either the Floer complex
 $CF^*(L_1,L_2)$
is
$CF^*(L_1,L_2)$
is
 $\mathbb {Z}/2$
-graded, which is always possible, or
$\mathbb {Z}/2$
-graded, which is always possible, or -
• it is
 $\mathbb {Z}$
-graded assuming that and the Lagrangians
$\mathbb {Z}$
-graded assuming that and the Lagrangians $$\begin{align*}2 c_1(\hat{W}) =0\end{align*}$$
$$\begin{align*}2 c_1(\hat{W}) =0\end{align*}$$
 $L_1$
and
$L_1$
and
 $L_2$
are graded in the sense of [Reference Seidel45, Section 12].
$L_2$
are graded in the sense of [Reference Seidel45, Section 12].
Later in Section 7 where the grading is not important, we will usually denote the Floer cochain complex just by
![]() $CF(L_1,L_2)$
without the superscript
$CF(L_1,L_2)$
without the superscript
![]() $^*$
.
$^*$
.
We remark that one can extend the action functional
![]() $\mathcal {A}$
(2.1) as a function defined on
$\mathcal {A}$
(2.1) as a function defined on
![]() $CF^*(L_1,L_2)$
as
$CF^*(L_1,L_2)$
as
 $$ \begin{align} \mathcal{A}\left(\sum_{x_i \in L_1 \cap L_2} a_i x_i\right) = \max\left\{\mathcal{A}(x_i) | a_i \neq 0\right\}. \end{align} $$
$$ \begin{align} \mathcal{A}\left(\sum_{x_i \in L_1 \cap L_2} a_i x_i\right) = \max\left\{\mathcal{A}(x_i) | a_i \neq 0\right\}. \end{align} $$
We need the extended action functional
![]() $\mathcal {A}$
in Section 7.
$\mathcal {A}$
in Section 7.
2.2 Partially wrapped Fukaya category
Let W be a Weinstein domain and let
![]() $(\hat {W},\omega =d\lambda )$
be the completion of W as in the previous subsection. The purpose of this subsection is to provide a brief introduction of partially wrapped Fukaya category associated with a stop of
$(\hat {W},\omega =d\lambda )$
be the completion of W as in the previous subsection. The purpose of this subsection is to provide a brief introduction of partially wrapped Fukaya category associated with a stop of
![]() $\hat {W}$
, mainly focusing on the definition of morphism space. There are two good references [Reference Ganatra, Pardon and Shende29], [Reference Sylvan47] for this topic. For convenience, we stick to the description given in [Reference Sylvan47]. A stop
$\hat {W}$
, mainly focusing on the definition of morphism space. There are two good references [Reference Ganatra, Pardon and Shende29], [Reference Sylvan47] for this topic. For convenience, we stick to the description given in [Reference Sylvan47]. A stop
![]() $\Lambda $
of
$\Lambda $
of
![]() $\hat {W}$
is a (possibly empty) hypersurface with boundary of
$\hat {W}$
is a (possibly empty) hypersurface with boundary of
![]() $\partial W$
(or equivalently
$\partial W$
(or equivalently
![]() $\partial _{\infty } \hat {W}$
) such that
$\partial _{\infty } \hat {W}$
) such that
![]() $\Lambda $
becomes a Liouville domain with the Liouville form
$\Lambda $
becomes a Liouville domain with the Liouville form
![]() $\lambda |_{\Lambda }$
.
$\lambda |_{\Lambda }$
.
Let
![]() $\Lambda \subset \partial W= \partial _{\infty } \hat {W}$
be a stop. The partially wrapped Fukaya category
$\Lambda \subset \partial W= \partial _{\infty } \hat {W}$
be a stop. The partially wrapped Fukaya category
![]() $\mathcal {W}(W,\Lambda )$
is an
$\mathcal {W}(W,\Lambda )$
is an
![]() $A_{\infty }$
-category associated with the pair
$A_{\infty }$
-category associated with the pair
![]() $(W,\Lambda )$
whose objects are cylindrical Lagrangians L of
$(W,\Lambda )$
whose objects are cylindrical Lagrangians L of
![]() $\hat {W}$
equipped with additional structures such as gradings, relative pin structures and local systems such that
$\hat {W}$
equipped with additional structures such as gradings, relative pin structures and local systems such that
![]() $L \cap \partial W \cap \Lambda =\emptyset $
.
$L \cap \partial W \cap \Lambda =\emptyset $
.
To define morphism spaces of
![]() $\mathcal {W}(W,\Lambda )$
, we consider quadratic Hamiltonians H on
$\mathcal {W}(W,\Lambda )$
, we consider quadratic Hamiltonians H on
![]() $\hat {W}$
that are compatible with the stop
$\hat {W}$
that are compatible with the stop
![]() $\Lambda $
in the sense of [Reference Sylvan47, Section 2.4]. Let us denote the set of all such Hamiltonians on
$\Lambda $
in the sense of [Reference Sylvan47, Section 2.4]. Let us denote the set of all such Hamiltonians on
![]() $\hat {W}$
by
$\hat {W}$
by
![]() $\mathcal {H}(\hat {W})$
. For any Hamiltonian H on
$\mathcal {H}(\hat {W})$
. For any Hamiltonian H on
![]() $\hat {W}$
, we denote the corresponding Hamiltonian vector field by
$\hat {W}$
, we denote the corresponding Hamiltonian vector field by
![]() $X_H$
, that is,
$X_H$
, that is,
![]() $X_H$
is a unique vector field on
$X_H$
is a unique vector field on
![]() $\hat {W}$
characterized by
$\hat {W}$
characterized by
We further consider an almost complex structure J that is compatible with
![]() $\omega $
and is of contact type as in the previous subsection.
$\omega $
and is of contact type as in the previous subsection.
Let
![]() $L_1$
and
$L_1$
and
![]() $L_2$
be Lagrangians that are allowed to be objects of
$L_2$
be Lagrangians that are allowed to be objects of
![]() $\mathcal {W}(W,\Lambda )$
. For a Hamiltonian
$\mathcal {W}(W,\Lambda )$
. For a Hamiltonian
![]() $H \in \mathcal {H}(\hat {W})$
, we define an action functional
$H \in \mathcal {H}(\hat {W})$
, we define an action functional
by
 $$\begin{align*}\mathcal{A}_{L_1,L_2,H} (\gamma) = -\int \gamma^*\lambda + \int_{0}^{1} H(\gamma(t))dt- h_1(\gamma(0)) + h_2(\gamma(1)).\end{align*}$$
$$\begin{align*}\mathcal{A}_{L_1,L_2,H} (\gamma) = -\int \gamma^*\lambda + \int_{0}^{1} H(\gamma(t))dt- h_1(\gamma(0)) + h_2(\gamma(1)).\end{align*}$$
As done in the previous subsection, it is easy to check that
-
• critical points of the action functional
 $\mathcal {A}_{L_1,L_2,H}$
are
$\mathcal {A}_{L_1,L_2,H}$
are
 $X_H$
-chords from
$X_H$
-chords from
 $L_1$
to
$L_1$
to
 $H_2$
, where an
$H_2$
, where an
 $X_H$
-chord from
$X_H$
-chord from
 $L_1$
to
$L_1$
to
 $L_2$
means a path
$L_2$
means a path
 $\gamma :[0,1]\to \hat {W}$
satisfying
$\gamma :[0,1]\to \hat {W}$
satisfying
 $\gamma (0)\in L_1$
,
$\gamma (0)\in L_1$
,
 $\gamma (1) \in L_2$
and
$\gamma (1) \in L_2$
and
 $\dot {\gamma }(t) = X_H(\gamma (t))$
, and
$\dot {\gamma }(t) = X_H(\gamma (t))$
, and -
• gradient flows are given by Floer strips
satisfying $$\begin{align*}u : \mathbb{R} \times [0,1] \to \hat{W}\end{align*}$$
and the Floer equation
$$\begin{align*}u : \mathbb{R} \times [0,1] \to \hat{W}\end{align*}$$
and the Floer equation $$\begin{align*}u(s,0) \in L_1, u(s,1)\in L_2, \forall s\in \mathbb{R}\end{align*}$$
$$\begin{align*}u(s,0) \in L_1, u(s,1)\in L_2, \forall s\in \mathbb{R}\end{align*}$$
 $$\begin{align*}\partial_s u+ J (\partial_t u - X_H(u)) =0 , \forall (s,t) \in \mathbb{R} \times [0,1].\end{align*}$$
$$\begin{align*}\partial_s u+ J (\partial_t u - X_H(u)) =0 , \forall (s,t) \in \mathbb{R} \times [0,1].\end{align*}$$
Let us denote by
![]() $\mathcal {X}(L_1,L_2;H)$
the set of all
$\mathcal {X}(L_1,L_2;H)$
the set of all
![]() $X_H$
-chords from
$X_H$
-chords from
![]() $L_1$
to
$L_1$
to
![]() $L_2$
. There is a function
$L_2$
. There is a function
![]() $n_{\Lambda } : \mathcal {X}(L_1,L_2;H) \to \mathbb {Z}_{\geq 0}$
defined by counting the intersection number of a given
$n_{\Lambda } : \mathcal {X}(L_1,L_2;H) \to \mathbb {Z}_{\geq 0}$
defined by counting the intersection number of a given
![]() $X_H$
-chord with the stop
$X_H$
-chord with the stop
![]() $\Lambda $
. We take
$\Lambda $
. We take
![]() $\mathcal {X}_0(L_1,L_2;H)$
to be
$\mathcal {X}_0(L_1,L_2;H)$
to be
![]() $n_{\Lambda }^{-1}(0)$
.
$n_{\Lambda }^{-1}(0)$
.
For a given field k, the partially wrapped Floer complex
![]() $CW_{\Lambda }^*(L_1,L_2)$
is defined as follows.
$CW_{\Lambda }^*(L_1,L_2)$
is defined as follows.
-
•
 $CW^*_{\Lambda }(L_1,L_2)$
is a graded k-vector space generated by elements of
$CW^*_{\Lambda }(L_1,L_2)$
is a graded k-vector space generated by elements of
 $\mathcal {X}_0(L_1,L_2;H)$
, and
$\mathcal {X}_0(L_1,L_2;H)$
, and -
• the differential is defined by counting Floer strips of index
 $1$
between two elements of
$1$
between two elements of
 $\mathcal {X}_0(L_1,L_2;H)$
.
$\mathcal {X}_0(L_1,L_2;H)$
.
It can be shown as in [Reference Sylvan47] that this indeed defines a cochain complex. We call the resulting cohomology the partially wrapped Floer cohomology between
![]() $L_1$
and
$L_1$
and
![]() $L_2$
with respect to the stop
$L_2$
with respect to the stop
![]() $\Lambda $
and denote it by
$\Lambda $
and denote it by
![]() $HW^*_{\Lambda }(L_1,L_2)$
.
$HW^*_{\Lambda }(L_1,L_2)$
.
There are two particularly interesting cases of a stop. The first one is the case
![]() $\Lambda =\emptyset $
. In this case, the corresponding
$\Lambda =\emptyset $
. In this case, the corresponding
![]() $CW^*_{\Lambda }(L_1,L_2)$
(resp.
$CW^*_{\Lambda }(L_1,L_2)$
(resp.
![]() $HW^*_{\Lambda }(L_1,L_2)$
) is called the wrapped Floer complex between
$HW^*_{\Lambda }(L_1,L_2)$
) is called the wrapped Floer complex between
![]() $L_1$
and
$L_1$
and
![]() $L_2$
(resp. wrapped Floer cohomology between
$L_2$
(resp. wrapped Floer cohomology between
![]() $L_1$
and
$L_1$
and
![]() $L_2$
.) and denoted by
$L_2$
.) and denoted by
![]() $CW^*(L_1,L_2)$
(resp.
$CW^*(L_1,L_2)$
(resp.
![]() $HW^*(L_1,L_2)$
).
$HW^*(L_1,L_2)$
).
The second one is the case when the partially wrapped Floer complex (or more generally, partially wrapped Fukaya category) is fully stopped. To be more precise, we define the notion of full-stop.
Definition 2.3. A stop
![]() $\Lambda $
is a full-stop if
$\Lambda $
is a full-stop if
![]() $HW^*_\Lambda (L_1,L_2)$
is of finite dimension for every pair
$HW^*_\Lambda (L_1,L_2)$
is of finite dimension for every pair
![]() $(L_1, L_2)$
.
$(L_1, L_2)$
.
We would like to note two things. The first one is the reason why the notion of full-stop is interesting. The reason is actually mentioned in Definition 2.3, that is, the morphism spaces have finite dimensional homologies. Equivalently, we can simply say that the corresponding partially wrapped Fukaya category is proper. This algebraic property plays a key role in the current article. Then, a question naturally arises, which is the second one we would like to note. The question asks the existence of full-stops. We note that for every Weinstein manifold, the existence is guaranteed. For example, see [Reference Ganatra, Pardon and Shende29, Section 8.6].
To complete an introduction of partially wrapped Fukaya category, we need to explain the
![]() $A_{\infty }$
-operations on it. Indeed, for a positive integer k, we call a disk with
$A_{\infty }$
-operations on it. Indeed, for a positive integer k, we call a disk with
![]() $(k+1)$
-boundary punctures a
$(k+1)$
-boundary punctures a
![]() $(k+1)$
-gon. We further label the boundary punctures with
$(k+1)$
-gon. We further label the boundary punctures with
![]() $\{1,\dots ,k+1 \ \mathrm {mod} \ k+2\}$
and call the boundary component between ith and
$\{1,\dots ,k+1 \ \mathrm {mod} \ k+2\}$
and call the boundary component between ith and
![]() $(i+1)$
-puncture the ith-boundary component for
$(i+1)$
-puncture the ith-boundary component for
![]() $1\leq i \leq k+1$
. For any collection
$1\leq i \leq k+1$
. For any collection
![]() $(L_1,\dots , L_{k+1})$
of Lagragians of W, the
$(L_1,\dots , L_{k+1})$
of Lagragians of W, the
![]() $A_\infty $
-operation
$A_\infty $
-operation
is defined by counting rigid Floer
![]() $(k+1)$
-gons, which map the ith boundary component to
$(k+1)$
-gons, which map the ith boundary component to
![]() $L_i$
and are asymptotic to an
$L_i$
and are asymptotic to an
![]() $X_H$
-chord from
$X_H$
-chord from
![]() $L_i$
to
$L_i$
to
![]() $L_{i+1}$
belonging to
$L_{i+1}$
belonging to
![]() $\mathcal {X}_0(L_i,L_{i+1};H)$
at the ith puncture for
$\mathcal {X}_0(L_i,L_{i+1};H)$
at the ith puncture for
![]() $1\leq i \leq k$
and an
$1\leq i \leq k$
and an
![]() $X_H$
-chord from
$X_H$
-chord from
![]() $L_1$
to
$L_1$
to
![]() $L_{k+1}$
at
$L_{k+1}$
at
![]() $k+1$
-th puncture. Here
$k+1$
-th puncture. Here
![]() $L_{k+2}$
is defined to be
$L_{k+2}$
is defined to be
![]() $L_1$
for simplicity. Especially the first operation
$L_1$
for simplicity. Especially the first operation
![]() $\mu ^1_{\Lambda }$
coincides with the differential on the partially wrapped Floer complex up to sign. Then the operations
$\mu ^1_{\Lambda }$
coincides with the differential on the partially wrapped Floer complex up to sign. Then the operations
![]() $\mu ^k_{\Lambda }$
’s satisfy the
$\mu ^k_{\Lambda }$
’s satisfy the
![]() $A_{\infty }$
-relations as shown in [Reference Sylvan47].
$A_{\infty }$
-relations as shown in [Reference Sylvan47].
The resulting
![]() $A_{\infty }$
-category is the partially wrapped Fukaya category
$A_{\infty }$
-category is the partially wrapped Fukaya category
![]() $\mathcal {W}(W,\Lambda )$
of the pair
$\mathcal {W}(W,\Lambda )$
of the pair
![]() $(W,\Lambda )$
. As done above, in the case
$(W,\Lambda )$
. As done above, in the case
![]() $\Lambda = \emptyset $
, the corresponding partially wrapped Fukaya category is called the wrapped Fukaya category of W and denoted by
$\Lambda = \emptyset $
, the corresponding partially wrapped Fukaya category is called the wrapped Fukaya category of W and denoted by
![]() $\mathcal {W}(W)$
. For future use in this paper, we further define the compact Fukaya category
$\mathcal {W}(W)$
. For future use in this paper, we further define the compact Fukaya category
![]() $\mathcal {F}(W)$
to be the full subcategory of
$\mathcal {F}(W)$
to be the full subcategory of
![]() $\mathcal {W}(W)$
generated by closed exact Lagrangian submanifolds of
$\mathcal {W}(W)$
generated by closed exact Lagrangian submanifolds of
![]() $\hat {W}$
.
$\hat {W}$
.
2.3 Topological entropy
Let X be a topological space and let
![]() $\phi : X \to X$
be a continuous self-mapping defined on X. The notion of topological entropy
$\phi : X \to X$
be a continuous self-mapping defined on X. The notion of topological entropy
![]() $h_{top}(\phi )$
is defined in [Reference Adler, Konheim and McAndrew2] for compact X and in [Reference Hofer32], [Reference Hofer33] for non-compact X.
$h_{top}(\phi )$
is defined in [Reference Adler, Konheim and McAndrew2] for compact X and in [Reference Hofer32], [Reference Hofer33] for non-compact X.
In particular, even though X is non-compact, if a continuous self-mapping
![]() $\phi : X \to X$
is compactly-supported and so its support is contained in a compact subspace
$\phi : X \to X$
is compactly-supported and so its support is contained in a compact subspace
![]() $X_0$
of X, then the following equality holds
$X_0$
of X, then the following equality holds
Since we only consider the topological entropy of compactly-supported smooth self-mappings on smooth manifolds in this paper, the above observation implies that it is enough to consider the topological entropy of a smooth self-mapping on a compact smooth manifold. Let X be a compact smooth manifold (with or without boundary) of dimension n equipped with a Riemannian metric g in the rest of Section 2.3. Then the following is a formulation of the topological entropy of a smooth map
![]() $\phi : X \to X$
due to Dinaburg [Reference Dinaburg19] and Bowen [Reference Bowen11].
$\phi : X \to X$
due to Dinaburg [Reference Dinaburg19] and Bowen [Reference Bowen11].
Definition 2.4 (Dinaburg, Bowen).
-
1. Let
 $\Gamma _\phi ^k$
denote the set of strings
$\Gamma _\phi ^k$
denote the set of strings  $$\begin{align*}\Gamma_{\phi}^k:=\Big\{\left(x, \phi(x), \dots, \phi^{k-1}(x)\right) \in X^k := X \times \dots \times X (k\text{ factors}\Big\}.\end{align*}$$
$$\begin{align*}\Gamma_{\phi}^k:=\Big\{\left(x, \phi(x), \dots, \phi^{k-1}(x)\right) \in X^k := X \times \dots \times X (k\text{ factors}\Big\}.\end{align*}$$
-
2. An
 $\epsilon $
-cubes in
$\epsilon $
-cubes in
 $X^k$
is a product of balls in X of radius
$X^k$
is a product of balls in X of radius
 $\epsilon $
.
$\epsilon $
. -
3. For a subset
 $Y \subset X^k$
,
$Y \subset X^k$
,
 $\text {Cap}_{\epsilon } Y$
is the minimal number of
$\text {Cap}_{\epsilon } Y$
is the minimal number of
 $\epsilon $
-cubes needed to cover Y.
$\epsilon $
-cubes needed to cover Y. -
4. The topological entropy of
 $\phi $
, denoted by
$\phi $
, denoted by
 $h_{top}(\phi )$
, is given by
$h_{top}(\phi )$
, is given by  $$\begin{align*}h_{top}(\phi) := \lim_{\epsilon \to 0} \limsup _{k \to \infty} \frac{1}{k} \log \mathrm{Cap}_{\epsilon} \Gamma_\phi^k.\end{align*}$$
$$\begin{align*}h_{top}(\phi) := \lim_{\epsilon \to 0} \limsup _{k \to \infty} \frac{1}{k} \log \mathrm{Cap}_{\epsilon} \Gamma_\phi^k.\end{align*}$$
Note that the
![]() $h_{top}(\phi )$
in Definition 2.4 (4) does not depend on a specific choice of a Riemannian metric g. See [Reference Bowen11], [Reference Dinaburg20] for more details on topological entropy.
$h_{top}(\phi )$
in Definition 2.4 (4) does not depend on a specific choice of a Riemannian metric g. See [Reference Bowen11], [Reference Dinaburg20] for more details on topological entropy.
We end this subsection by stating a property of topological entropy that plays a key role in the proof of Lemma 3.4. For a
![]() $C^\infty $
-submanifold
$C^\infty $
-submanifold
![]() $Y \subset X$
of dimension m, let
$Y \subset X$
of dimension m, let
We note that the product metric on
![]() $X^k$
induces an m-dimensional volume form. Thus, we can measure the volumes of
$X^k$
induces an m-dimensional volume form. Thus, we can measure the volumes of
![]() $\Gamma _{\phi |_Y}^k$
for all k. The following is a significant observation due to Yomdin that the exponential growth rate of the volumes is a lower bound of
$\Gamma _{\phi |_Y}^k$
for all k. The following is a significant observation due to Yomdin that the exponential growth rate of the volumes is a lower bound of
![]() $h_{top}(\phi )$
.
$h_{top}(\phi )$
.
Theorem 2.5 (Yomdin).
The topological entropy of
![]() $\phi $
is bounded by the exponential growth rate of the volume of
$\phi $
is bounded by the exponential growth rate of the volume of
![]() $\Gamma _{\phi |_Y}^k$
, that is,
$\Gamma _{\phi |_Y}^k$
, that is,
 $$\begin{align*}\limsup_{k \to \infty} \frac{1}{k} \log \mathrm{Vol}(\Gamma_{\phi|_Y}^k) \leq h_{top}(\phi).\end{align*}$$
$$\begin{align*}\limsup_{k \to \infty} \frac{1}{k} \log \mathrm{Vol}(\Gamma_{\phi|_Y}^k) \leq h_{top}(\phi).\end{align*}$$
See [Reference Gromov30], [Reference Yomdin50] for the proof of Theorem 2.5.
2.4 Categorical entropy
In this subsection, we introduce the notion of categorical entropy. This requires preliminary knowledge on triangulated categories, split-generators, etc. We recommend [Reference Gelfand and Manin27], [Reference Seidel45] as a general reference on these. We start by introducing the notions of complexity and categorical entropy, which are originally defined in [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18].
Definition 2.6. Let
![]() $\mathcal {C}$
be a triangulated category with a split-generator G. Let
$\mathcal {C}$
be a triangulated category with a split-generator G. Let
![]() $\Phi $
be an auto-equivalence defined on
$\Phi $
be an auto-equivalence defined on
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
-
1. The complexity of
 $E_2$
relative to
$E_2$
relative to
 $E_1$
at t is a number in
$E_1$
at t is a number in
 $[0,\infty ]$
given by
$[0,\infty ]$
given by 
-
2. For a given
 $t\in \mathbb {R}$
, the categorical entropy of
$t\in \mathbb {R}$
, the categorical entropy of
 $\Phi $
at t is defined as
$\Phi $
at t is defined as  $$\begin{align*}h_{cat}(\Phi;t):=\lim_{n\to\infty}\frac{1}{n}\log\delta_t(G;\Phi^n(G))\in \{-\infty\}\cup \mathbb{R}.\end{align*}$$
$$\begin{align*}h_{cat}(\Phi;t):=\lim_{n\to\infty}\frac{1}{n}\log\delta_t(G;\Phi^n(G))\in \{-\infty\}\cup \mathbb{R}.\end{align*}$$
In the current paper, we only consider the case of
![]() $t=0$
.
$t=0$
.
Definition 2.7. Let
![]() $\Phi : \mathcal {C} \to \mathcal {C}$
be an auto-equivalence defined on a triangulated category
$\Phi : \mathcal {C} \to \mathcal {C}$
be an auto-equivalence defined on a triangulated category
![]() $\mathcal {C}$
with a generator G. We define the categorical entropy of
$\mathcal {C}$
with a generator G. We define the categorical entropy of
![]() $\Phi $
as
$\Phi $
as
Remark 2.8. We note that
![]() $h_{cat}(\Phi ) = h_{cat}(\Phi ;0) \geq 0$
by definition.
$h_{cat}(\Phi ) = h_{cat}(\Phi ;0) \geq 0$
by definition.
Let
![]() $\mathcal {D}$
be a fully faithful subcategory of
$\mathcal {D}$
be a fully faithful subcategory of
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
-
•
 $\mathcal {D}$
is a triangulated category, and
$\mathcal {D}$
is a triangulated category, and -
• the restriction of
 $\Phi $
to
$\Phi $
to
 $\mathcal {D}$
defines an auto-equivalence on
$\mathcal {D}$
defines an auto-equivalence on
 $\mathcal {D}$
, that is,
$\mathcal {D}$
, that is,
 $\Phi (\mathcal {D}) \subset \mathcal {D}$
.
$\Phi (\mathcal {D}) \subset \mathcal {D}$
.
It is known that there exists a localization functor l
See [Reference Drinfeld21]. Then,
![]() $\Phi $
induces an auto-equivalence defined on
$\Phi $
induces an auto-equivalence defined on
![]() $\mathcal {C}/\mathcal {D}$
uniquely up to natural transformations. More precisely, there exists a unique (up to natural transformation) dg functor
$\mathcal {C}/\mathcal {D}$
uniquely up to natural transformations. More precisely, there exists a unique (up to natural transformation) dg functor
satisfying
To be clear, let us use the following notations
![]() $\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}$
, and
$\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}$
, and
![]() $\Phi _{\mathcal {C}/\mathcal {D}}$
,
$\Phi _{\mathcal {C}/\mathcal {D}}$
,
Then, [Reference Bae, Choa, Jeong, Karabas and Lee9, Theorem 3.8] compares the categorical entropies of
![]() $\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}$
, and
$\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}$
, and
![]() $\Phi _{\mathcal {C}/\mathcal {D}}$
.
$\Phi _{\mathcal {C}/\mathcal {D}}$
.
Lemma 2.9 [Reference Bae, Choa, Jeong, Karabas and Lee9, Theorem 3.10].
The categorical entropies of
![]() $\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}, \Phi _{\mathcal {C}/\mathcal {D}}$
satisfy
$\Phi _{\mathcal {C}}, \Phi _{\mathcal {D}}, \Phi _{\mathcal {C}/\mathcal {D}}$
satisfy
Let
![]() $\hat {W}$
be a Weinstein manifold. Then let
$\hat {W}$
be a Weinstein manifold. Then let
![]() $W \subset \hat {W}$
be an associated Weinstein domain and let
$W \subset \hat {W}$
be an associated Weinstein domain and let
![]() $\Lambda $
be a stop in
$\Lambda $
be a stop in
![]() $\partial W=\partial _\infty \hat {W}$
. Let
$\partial W=\partial _\infty \hat {W}$
. Let
![]() $\phi : \hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism and. Then
$\phi : \hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism and. Then
![]() $\phi $
induces functors
$\phi $
induces functors
![]() $\Phi : \mathcal {W}(W) \to \mathcal {W}(W)$
and
$\Phi : \mathcal {W}(W) \to \mathcal {W}(W)$
and
![]() $\Phi _\Lambda : \mathcal {W}(W,\Lambda ) \to \mathcal {W}(W,\Lambda )$
. Thanks to Lemma 2.9, one can compare
$\Phi _\Lambda : \mathcal {W}(W,\Lambda ) \to \mathcal {W}(W,\Lambda )$
. Thanks to Lemma 2.9, one can compare
![]() $h_{cat}(\Phi )$
and
$h_{cat}(\Phi )$
and
![]() $h_{cat}(\Phi _\Lambda )$
.
$h_{cat}(\Phi _\Lambda )$
.
Lemma 2.10 [Reference Bae, Choa, Jeong, Karabas and Lee9, Theorem 1.2].
The induced functors
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi _\Lambda $
have the same categorical entropy, that is,
$\Phi _\Lambda $
have the same categorical entropy, that is,
Proof. We note that
where
![]() $\mathcal {D}$
means the full subcategory of
$\mathcal {D}$
means the full subcategory of
![]() $\mathcal {W}(W,\Lambda )$
generated by all linking disks. Here linking disks are certain cylindrical Lagrangian disks of
$\mathcal {W}(W,\Lambda )$
generated by all linking disks. Here linking disks are certain cylindrical Lagrangian disks of
![]() $\hat {W}$
associated with
$\hat {W}$
associated with
![]() $\Lambda $
, for which the intersection with the domain W can be chosen to lie arbitrarily close to
$\Lambda $
, for which the intersection with the domain W can be chosen to lie arbitrarily close to
![]() $\Lambda \subset \partial W$
. See [Reference Ganatra, Pardon and Shende29, Section 5] for a definition of linking disk.
$\Lambda \subset \partial W$
. See [Reference Ganatra, Pardon and Shende29, Section 5] for a definition of linking disk.
Since
![]() $\phi $
is compactly supported, the restriction of
$\phi $
is compactly supported, the restriction of
![]() $\Phi $
on
$\Phi $
on
![]() $\mathcal {D}$
is the identity functor. Thus, the categorical entropy of
$\mathcal {D}$
is the identity functor. Thus, the categorical entropy of
![]() $\Phi |_{\mathcal {D}}$
is zero.
$\Phi |_{\mathcal {D}}$
is zero.
We note that, as mentioned Remark 2.8,
By applying Lemma 2.9, one has
This completes the proof.
Remark 2.11. In Section 1, we used the notation
![]() $h_{cat}(\phi )$
to denote
$h_{cat}(\phi )$
to denote
![]() $h_{cat} (\Phi )$
where
$h_{cat} (\Phi )$
where
![]() $\Phi $
is the induced auto-equivalence on the wrapped Fukaya category of
$\Phi $
is the induced auto-equivalence on the wrapped Fukaya category of
![]() $\hat {W}$
. In the above, we have seen that
$\hat {W}$
. In the above, we have seen that
![]() $\phi $
induces an auto-equivalence
$\phi $
induces an auto-equivalence
![]() $\Phi $
on the wrapped Fukaya category
$\Phi $
on the wrapped Fukaya category
![]() $\mathcal {W}(W)$
and an auto-equivalence
$\mathcal {W}(W)$
and an auto-equivalence
![]() $\Phi _{\Lambda }$
on the partially wrapped Fukaya category
$\Phi _{\Lambda }$
on the partially wrapped Fukaya category
![]() $\mathcal {W}(W,\Lambda )$
. In order to avoid confusion, we let
$\mathcal {W}(W,\Lambda )$
. In order to avoid confusion, we let
![]() $h_{cat}(\Phi )$
(resp.
$h_{cat}(\Phi )$
(resp.
![]() $h_{cat}(\Phi _{\Lambda })$
) denote the categorical entropy of
$h_{cat}(\Phi _{\Lambda })$
) denote the categorical entropy of
![]() $\Phi $
on
$\Phi $
on
![]() $\mathcal {W}(W)$
(resp.
$\mathcal {W}(W)$
(resp.
![]() $\Phi _{\Lambda }$
on
$\Phi _{\Lambda }$
on
![]() $\mathcal {W}(W, \Lambda )$
).
$\mathcal {W}(W, \Lambda )$
).
3 Crofton’s inequality
The goal of this section is to prove Lemma 3.4 which plays a key role in the proof of Theorem 1.2. In order to prove Lemma 3.4, we construct a family of Lagrangian submanifolds satisfying some conditions in Lemma 3.2. By using the family of Lagrangians, we prove Lemma 3.4 in Section 3.2.
3.1 Lagrangian tomograph
Let
![]() $(\hat {W},d\lambda )$
be a Weinstein manifold and let
$(\hat {W},d\lambda )$
be a Weinstein manifold and let
![]() $W \subset \hat {W}$
be a Weinstein domain in the rest of this section. In many places of this paper, we consider pairs of Lagrangians in
$W \subset \hat {W}$
be a Weinstein domain in the rest of this section. In many places of this paper, we consider pairs of Lagrangians in
![]() $\hat {W}$
satisfying the following condition.
$\hat {W}$
satisfying the following condition.
Definition 3.1. A pair of Lagrangians
![]() $(L_1, L_2)$
in
$(L_1, L_2)$
in
![]() $\hat {W}$
is good if
$\hat {W}$
is good if
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are disjoint in the cylindrical part, that is,
$L_2$
are disjoint in the cylindrical part, that is,
For a good pair of Lagrangians, we construct a Lagrangian tomograph in Lemma 3.2. The original construction of Lagrangian tomograph is given in [Reference Cineli, Ginzburg and Gürel13, Section 5.2.3], and our construction is a slight modification of the original one.
Lemma 3.2. Let
![]() $(L_1, L_2)$
be a good pair of Lagrangians in
$(L_1, L_2)$
be a good pair of Lagrangians in
![]() $\hat {W}$
. Then, for any
$\hat {W}$
. Then, for any
![]() $\epsilon>0$
and sufficiently large
$\epsilon>0$
and sufficiently large
![]() $d \in \mathbb {N}$
, there is a sufficiently small
$d \in \mathbb {N}$
, there is a sufficiently small
![]() $\delta>0$
and a family of Lagrangians
$\delta>0$
and a family of Lagrangians
![]() $\{L^s\}_{s \in B_\epsilon ^d}$
, where
$\{L^s\}_{s \in B_\epsilon ^d}$
, where
![]() $B_\epsilon ^d$
is a d-dimensional closed ball of radius
$B_\epsilon ^d$
is a d-dimensional closed ball of radius
![]() $\delta $
in the Euclidean space, such that
$\delta $
in the Euclidean space, such that
-
(i)
 $L_1$
and
$L_1$
and
 $L^s$
are Hamiltonian isotopic to each other for all
$L^s$
are Hamiltonian isotopic to each other for all
 $s \in B_\epsilon ^d$
,
$s \in B_\epsilon ^d$
, -
(ii)
 $d_H(L_1, L^s) < \frac {\epsilon }{2}$
for all
$d_H(L_1, L^s) < \frac {\epsilon }{2}$
for all
 $s \in B^d_\epsilon $
, and
$s \in B^d_\epsilon $
, and -
(iii)
 $L^s$
and
$L^s$
and
 $L_2$
intersect transversely for almost all
$L_2$
intersect transversely for almost all
 $s \in B_\epsilon ^d$
.
$s \in B_\epsilon ^d$
.
We note that the radius of the ball
![]() $B_\epsilon ^d$
in the above lemma is
$B_\epsilon ^d$
in the above lemma is
![]() $\delta $
, not
$\delta $
, not
![]() $\epsilon $
. The reason why we use the notation is explained in Remark 3.3.
$\epsilon $
. The reason why we use the notation is explained in Remark 3.3.
Before going further, we briefly review the notion of Hofer norm
![]() $d_H$
of a Hamiltonian isotopy, which appears in the condition (ii) of Lemma 3.2. Let
$d_H$
of a Hamiltonian isotopy, which appears in the condition (ii) of Lemma 3.2. Let
![]() $\varphi $
be a compactly supported Hamiltonian isotopy. Then, the Hofer norm of
$\varphi $
be a compactly supported Hamiltonian isotopy. Then, the Hofer norm of
![]() $\varphi $
is defined as
$\varphi $
is defined as
 $$\begin{align*}\lVert \varphi \rVert_{Hofer} := \inf_H \int_{S^1} (\max_M H_t - \min_M H_t)dt,\end{align*}$$
$$\begin{align*}\lVert \varphi \rVert_{Hofer} := \inf_H \int_{S^1} (\max_M H_t - \min_M H_t)dt,\end{align*}$$
where the infimum is taken over all
![]() $1$
-periodic, time-dependent Hamiltonian H generating
$1$
-periodic, time-dependent Hamiltonian H generating
![]() $\varphi $
. Moreover, one can define the Hofer distance between two Hamiltonian isotopic Lagrangians L and
$\varphi $
. Moreover, one can define the Hofer distance between two Hamiltonian isotopic Lagrangians L and
![]() $L'$
as
$L'$
as
Proof of Lemma 3.2.
Since
![]() $(L_1,L_2)$
is a good pair, there is a submanifold
$(L_1,L_2)$
is a good pair, there is a submanifold
![]() $W_0 \subset W$
of codimension 0 whose closure is compact such that
$W_0 \subset W$
of codimension 0 whose closure is compact such that
where
![]() $\mathrm {Int}(W_0)$
and
$\mathrm {Int}(W_0)$
and
![]() $\mathrm {Int}(W)$
denote the interiors of
$\mathrm {Int}(W)$
denote the interiors of
![]() $W_0$
and W, respectively. Then, we choose a collection of real-valued functions
$W_0$
and W, respectively. Then, we choose a collection of real-valued functions
satisfying
-
(A)
 $g_i(x)=0$
if
$g_i(x)=0$
if
 $x \in L_1 \setminus W$
, and
$x \in L_1 \setminus W$
, and -
(B) for all
 $x \in L_1 \cap W_0$
, the cotangent fiber
$x \in L_1 \cap W_0$
, the cotangent fiber
 $T^*_xL_1$
is generated by
$T^*_xL_1$
is generated by
 $\{dg_i(x) | i =1, \dots , d\}$
.
$\{dg_i(x) | i =1, \dots , d\}$
.
For any
![]() $s = (s_1, \dots , s_d) \in \mathbb {R}^d$
, We set
$s = (s_1, \dots , s_d) \in \mathbb {R}^d$
, We set
 $$ \begin{align*} & f_s: L_1 \to \mathbb{R}, \\ x \mapsto s_1 g_1&(x) + \dots + s_d g_d(x). \end{align*} $$
$$ \begin{align*} & f_s: L_1 \to \mathbb{R}, \\ x \mapsto s_1 g_1&(x) + \dots + s_d g_d(x). \end{align*} $$
We note that there is a small neighborhood U of
![]() $L_1$
in
$L_1$
in
![]() $\hat {W}$
, which is symplectomorphic to a small disk cotangent bundle of
$\hat {W}$
, which is symplectomorphic to a small disk cotangent bundle of
![]() $L_1$
. We call U a Weinstein neighborhood of
$L_1$
. We call U a Weinstein neighborhood of
![]() $L_1$
. Then for
$L_1$
. Then for
![]() $s \in \mathbb {R}^d$
such that
$s \in \mathbb {R}^d$
such that
![]() $\lVert s \rVert \ll 1$
, one can assume that the graph of
$\lVert s \rVert \ll 1$
, one can assume that the graph of
![]() $df_s$
is embedded into
$df_s$
is embedded into
![]() $\hat {W}$
. Let
$\hat {W}$
. Let
![]() $L^s$
be the embedded image of the graph of
$L^s$
be the embedded image of the graph of
![]() $df_s$
in
$df_s$
in
![]() $\hat {W}$
. By the construction of
$\hat {W}$
. By the construction of
![]() $L^s$
, (i) holds obviously.
$L^s$
, (i) holds obviously.
Then, one can observe that (ii) holds for all
![]() $s \in \mathbb {R}^d$
sufficiently close to the origin. Let
$s \in \mathbb {R}^d$
sufficiently close to the origin. Let
![]() $\delta>0$
be a sufficiently small number such that if
$\delta>0$
be a sufficiently small number such that if
![]() $\lVert s \rVert < \delta $
, then (ii) holds. Let
$\lVert s \rVert < \delta $
, then (ii) holds. Let
![]() $B_\epsilon ^d \subset \mathbb {R}^d$
be the ball of radius
$B_\epsilon ^d \subset \mathbb {R}^d$
be the ball of radius
![]() $\delta $
centered at the origin.
$\delta $
centered at the origin.
In order to prove (iii), we show that the following map
![]() $\Psi $
is submersive at every point of
$\Psi $
is submersive at every point of
![]() $\Psi ^{-1}(L_2)$
:
$\Psi ^{-1}(L_2)$
:
 $$ \begin{align} & \Psi: B^d_\epsilon \times L_1 \to \hat{W}, \\ & \notag (s,x) \mapsto df_s(x). \end{align} $$
$$ \begin{align} & \Psi: B^d_\epsilon \times L_1 \to \hat{W}, \\ & \notag (s,x) \mapsto df_s(x). \end{align} $$
In other words, if
![]() $\Psi (s,x) \in L_2$
for some
$\Psi (s,x) \in L_2$
for some
![]() $(s,x) \in B^d_\epsilon \times L_1$
, we show that
$(s,x) \in B^d_\epsilon \times L_1$
, we show that
is surjective. Then it will follow that
![]() $L^s$
and
$L^s$
and
![]() $L_2$
intersect transversely for almost all
$L_2$
intersect transversely for almost all
![]() $s\in B_\epsilon ^d$
, that is, (iii) holds.
$s\in B_\epsilon ^d$
, that is, (iii) holds.
We equip
![]() $\hat {W}$
with a Riemannian metric g compatible with the Weinstein neighborhood of
$\hat {W}$
with a Riemannian metric g compatible with the Weinstein neighborhood of
![]() $L_1$
in the following sense. Indeed, note that any Riemannian metric
$L_1$
in the following sense. Indeed, note that any Riemannian metric
![]() $g_{L_1}$
on
$g_{L_1}$
on
![]() $L_1$
determines a natural Riemannian metric on its contangent bundle
$L_1$
determines a natural Riemannian metric on its contangent bundle
![]() $T^*L_1$
. Then identifying the Weinstein neighborhood U with a disk subbundle of
$T^*L_1$
. Then identifying the Weinstein neighborhood U with a disk subbundle of
![]() $T^*L_1$
, we require that the restriction of g to U coincides with the unique natural Riemmanian metric induced by the Riemannian metric
$T^*L_1$
, we require that the restriction of g to U coincides with the unique natural Riemmanian metric induced by the Riemannian metric
![]() $g_{L_1} := g|_{L_1}$
in the above sense. This is always possible.
$g_{L_1} := g|_{L_1}$
in the above sense. This is always possible.
Now let
where
![]() $d(x,y)$
is the distance function with respect to the Riemannian metric g. Since both
$d(x,y)$
is the distance function with respect to the Riemannian metric g. Since both
![]() $L_1\cap (W\setminus \mathrm {Int}(W_0))$
and
$L_1\cap (W\setminus \mathrm {Int}(W_0))$
and
![]() $L_2\cap (W\setminus \mathrm {Int}(W_0))$
are compact and
$L_2\cap (W\setminus \mathrm {Int}(W_0))$
are compact and
![]() $L_1 \cap L_2 \subset \mathrm {Int}(W_0)$
,
$L_1 \cap L_2 \subset \mathrm {Int}(W_0)$
,
![]() $\ell $
is well-defined and positive.
$\ell $
is well-defined and positive.
Consider the Riemannian metric on
![]() $L_1$
given by the restriction of g. Let us denote by
$L_1$
given by the restriction of g. Let us denote by
![]() $\lVert \cdot \rVert $
the corresponding norm on
$\lVert \cdot \rVert $
the corresponding norm on
![]() $T^*_xL_1$
. If the radius
$T^*_xL_1$
. If the radius
![]() $\delta $
is sufficiently small, then
$\delta $
is sufficiently small, then
![]() $\lVert df_s(x) \rVert < \ell $
for all
$\lVert df_s(x) \rVert < \ell $
for all
![]() $(s,x) \in B^d_\epsilon \times W$
since
$(s,x) \in B^d_\epsilon \times W$
since
![]() $g_i$
’s are compactly supported. We assume that
$g_i$
’s are compactly supported. We assume that
![]() $\delta $
is sufficiently small in this sense in the rest of the proof.
$\delta $
is sufficiently small in this sense in the rest of the proof.
Now assume that
![]() $\Psi (s,x) \in L_2$
for some
$\Psi (s,x) \in L_2$
for some
![]() $(s,x)\in B^{d}_\epsilon \times L_1$
. If
$(s,x)\in B^{d}_\epsilon \times L_1$
. If
![]() $\Psi (s,x) \in \hat {W} \setminus W$
, then
$\Psi (s,x) \in \hat {W} \setminus W$
, then
![]() $\Psi (s,x) \in L_1$
since
$\Psi (s,x) \in L_1$
since
![]() $g_i$
’s are assumed to be zero over
$g_i$
’s are assumed to be zero over
![]() $\hat {W} \setminus W$
by (A). This contradicts to the assumption
$\hat {W} \setminus W$
by (A). This contradicts to the assumption
![]() $L_1 \cap L_2 \subset W_0 \subset W$
. Otherwise, if
$L_1 \cap L_2 \subset W_0 \subset W$
. Otherwise, if
![]() $\Psi (s,x) \in W \setminus \mathrm {Int}(W_0)$
, then
$\Psi (s,x) \in W \setminus \mathrm {Int}(W_0)$
, then
![]() $d(\Psi (s,x),x) = \lVert df_s(x) \rVert < \ell $
, which follows from our choice of the Riemannian metric g. But, this contradicts to Equation (3.2).
$d(\Psi (s,x),x) = \lVert df_s(x) \rVert < \ell $
, which follows from our choice of the Riemannian metric g. But, this contradicts to Equation (3.2).
The above paragraph shows that if
![]() $\Psi (s,x) \in L_2$
, then
$\Psi (s,x) \in L_2$
, then
![]() $\Psi (s,x) \in W_0$
, that is,
$\Psi (s,x) \in W_0$
, that is,
![]() $L^s \cap L_2 \subset W_0$
. By the assumption (B), this means that
$L^s \cap L_2 \subset W_0$
. By the assumption (B), this means that
![]() $\Psi $
is submersive at every point in
$\Psi $
is submersive at every point in
![]() $\Psi ^{-1}(L_2)$
.
$\Psi ^{-1}(L_2)$
.
Remark 3.3. We also note that the the radius
![]() $\delta $
of
$\delta $
of
![]() $B^d_\epsilon $
in Lemma 3.2 is determined by
$B^d_\epsilon $
in Lemma 3.2 is determined by
![]() $\ell , \epsilon $
, and the collection
$\ell , \epsilon $
, and the collection
![]() $\{g_1, \dots , g_d\}$
. Among these factors, we would like to emphasize the effect of
$\{g_1, \dots , g_d\}$
. Among these factors, we would like to emphasize the effect of
![]() $\epsilon $
since in Section 7, we will vary
$\epsilon $
since in Section 7, we will vary
![]() $\epsilon $
and observe the effect to define the notion of barcode entropy. It is the reason why we use the notation
$\epsilon $
and observe the effect to define the notion of barcode entropy. It is the reason why we use the notation
![]() $B_\epsilon ^d$
.
$B_\epsilon ^d$
.
3.2 Crofton’s inequality
In Section 3.2, we prove Lemma 3.4, that is, a Crofton type inequality, which plays a key role in the proof of Theorem 1.2.
In order to state Lemma 3.4, we need some preparation. For
![]() $s \in B^d_\epsilon $
such that
$s \in B^d_\epsilon $
such that
![]() $L^s \pitchfork L_2$
, let
$L^s \pitchfork L_2$
, let
Then,
![]() $N(s)$
is finite for almost all
$N(s)$
is finite for almost all
![]() $s \in B^d_\epsilon $
. Moreover,
$s \in B^d_\epsilon $
. Moreover,
![]() $N(s)$
is an integrable function on
$N(s)$
is an integrable function on
![]() $B^d_\epsilon $
.
$B^d_\epsilon $
.
Since
![]() $B^d_\epsilon \subset \mathbb {R}^d$
,
$B^d_\epsilon \subset \mathbb {R}^d$
,
![]() $B^d_\epsilon $
carries the standard Euclidean metric. Let
$B^d_\epsilon $
carries the standard Euclidean metric. Let
![]() $ds$
be the volume form on
$ds$
be the volume form on
![]() $B^d_\epsilon $
induced by the Euclidean metric.
$B^d_\epsilon $
induced by the Euclidean metric.
Let
Then, let us fix a metric
![]() $g_E$
on E such that the restriction of
$g_E$
on E such that the restriction of
![]() $D\Psi $
to the normals to
$D\Psi $
to the normals to
![]() $\Psi ^{-1}(y), y \in W$
is an isometry. Since
$\Psi ^{-1}(y), y \in W$
is an isometry. Since
![]() $\Psi $
is a proper submersion,
$\Psi $
is a proper submersion,
![]() $\Psi $
is a locally trivial fibration by Ehresmann’s fibration theorem [Reference Ehresmann22]. Thus, the existence of such a metric is guaranteed.
$\Psi $
is a locally trivial fibration by Ehresmann’s fibration theorem [Reference Ehresmann22]. Thus, the existence of such a metric is guaranteed.
Now, we state Lemma 3.4.
Lemma 3.4. The following inequality holds:
 $$ \begin{align} \int_{B^d_\epsilon} N(s) ds \leq C \cdot \mathrm{Vol}(L_2 \cap W), \end{align} $$
$$ \begin{align} \int_{B^d_\epsilon} N(s) ds \leq C \cdot \mathrm{Vol}(L_2 \cap W), \end{align} $$
where C is a constant depending only on
![]() $\Psi , ds$
, the fixed metric g on
$\Psi , ds$
, the fixed metric g on
![]() $\hat {W}$
, and the fixed metric
$\hat {W}$
, and the fixed metric
![]() $g_E$
on E.
$g_E$
on E.
Proof. Let
![]() $\Sigma := \Psi ^{-1}(L_2 \cap W)$
. Then, by definition, for all
$\Sigma := \Psi ^{-1}(L_2 \cap W)$
. Then, by definition, for all
![]() $s \in B_{\epsilon }^d$
such that
$s \in B_{\epsilon }^d$
such that
![]() $L^s \pitchfork L_2$
, one has
$L^s \pitchfork L_2$
, one has
Note that in the proof of Lemma 3.2, we have
by choosing a sufficiently small
![]() $B^d_\epsilon $
.
$B^d_\epsilon $
.
We recall that
![]() $B^d_\epsilon $
carries the Euclidean metric and
$B^d_\epsilon $
carries the Euclidean metric and
![]() $L_1$
also carries a metric
$L_1$
also carries a metric
![]() $g|_{L_1}$
. Thus,
$g|_{L_1}$
. Thus,
![]() $B^d_\epsilon \times L_1$
carries a product metric. On E, the restriction of the product metric gives another metric that does not need to be the same as
$B^d_\epsilon \times L_1$
carries a product metric. On E, the restriction of the product metric gives another metric that does not need to be the same as
![]() $g_E$
.
$g_E$
.
Let
![]() $\pi : E \hookrightarrow B^d_\epsilon \times L_1 \to B^d_\epsilon $
be the projection to the first factor. Then, if
$\pi : E \hookrightarrow B^d_\epsilon \times L_1 \to B^d_\epsilon $
be the projection to the first factor. Then, if
![]() $\mathrm {Vol}_1(\cdot )$
denotes the volume with respect to the product metric on E, one has
$\mathrm {Vol}_1(\cdot )$
denotes the volume with respect to the product metric on E, one has
 $$ \begin{align} \int_{B^d_\epsilon} N(s) ds = \int_{B^d_\epsilon} |(s \times L_1) \cap \Sigma |ds = \int_{\Sigma} \pi^*ds \leq \mathrm{Vol}_1(\Sigma). \end{align} $$
$$ \begin{align} \int_{B^d_\epsilon} N(s) ds = \int_{B^d_\epsilon} |(s \times L_1) \cap \Sigma |ds = \int_{\Sigma} \pi^*ds \leq \mathrm{Vol}_1(\Sigma). \end{align} $$
Let
![]() $\mathrm {Vol}(\cdot )$
(resp.
$\mathrm {Vol}(\cdot )$
(resp.
![]() $\mathrm {Vol}_2(\cdot )$
) denote the volume with respect to the fixed metric g (resp.
$\mathrm {Vol}_2(\cdot )$
) denote the volume with respect to the fixed metric g (resp.
![]() $g_E$
) on W (resp. E). Then, by Fubini theorem, one has
$g_E$
) on W (resp. E). Then, by Fubini theorem, one has
 $$ \begin{align} \mathrm{Vol}_2(\Sigma) = \int_{L_2 \cap W} \mathrm{Vol}_2 \left(\Psi^{-1}(y)\right) dy|_{L_2} \leq \max_{y \in \Psi(E)} \mathrm{Vol}_2\left(\Psi^{-1}(y)\right) \cdot \mathrm{Vol}(L_2 \cap W). \end{align} $$
$$ \begin{align} \mathrm{Vol}_2(\Sigma) = \int_{L_2 \cap W} \mathrm{Vol}_2 \left(\Psi^{-1}(y)\right) dy|_{L_2} \leq \max_{y \in \Psi(E)} \mathrm{Vol}_2\left(\Psi^{-1}(y)\right) \cdot \mathrm{Vol}(L_2 \cap W). \end{align} $$
We note that since E is compact,
where
![]() $C_0$
is a constant depending only on
$C_0$
is a constant depending only on
![]() $g_E$
and the product metric on E.
$g_E$
and the product metric on E.
By combining Equations 3.4–3.6, one concludes that
 $$\begin{align*}\int_{B^d_\epsilon} N(s) ds \leq C \cdot \mathrm{Vol}(L_2 \cap W),\end{align*}$$
$$\begin{align*}\int_{B^d_\epsilon} N(s) ds \leq C \cdot \mathrm{Vol}(L_2 \cap W),\end{align*}$$
where C is a constant depending only on
![]() $\Psi , ds, g$
, and
$\Psi , ds, g$
, and
![]() $g_E$
.
$g_E$
.
Remark 3.5. We note that Lemma 3.4 is a slight modification of [Reference Cineli, Ginzburg and Gürel13, Lemma 5.3]. The original Crofton’s inequality is proven in [Reference Arnol’d6], [Reference Arnol’d7]. The reader can find additional context on Crofton’s inequality in [Reference Cineli, Ginzburg and Gürel13, Section 5.2.1], especially after [Reference Cineli, Ginzburg and Gürel13, Remark 5.4], and in references therein.
4 Categorical vs topological entropy
In this Section, we prove our main theorem comparing categorical and topological entropy. To be more precise, let
![]() $(\hat {W},d\lambda )$
be a Weinstein manifold and let
$(\hat {W},d\lambda )$
be a Weinstein manifold and let
![]() $W\subset \hat {W}$
be an associated Weinstein domain. Let
$W\subset \hat {W}$
be an associated Weinstein domain. Let
![]() $\phi :\hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism of
$\phi :\hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism of
![]() $\hat {W}$
. Let
$\hat {W}$
. Let
![]() $\Phi :\mathcal {W}(W) \to \mathcal {W}(W)$
denote the functor induced by
$\Phi :\mathcal {W}(W) \to \mathcal {W}(W)$
denote the functor induced by
![]() $\phi $
. Then, we prove Theorem 4.1.
$\phi $
. Then, we prove Theorem 4.1.
Theorem 4.1 (=Theorem 1.2).
The categorical entropy of
![]() $\Phi $
bounds the topological entropy of
$\Phi $
bounds the topological entropy of
![]() $\phi $
from below, that is,
$\phi $
from below, that is,
Proof. In order to prove Theorem 4.1, we recall that every Weinstein manifold
![]() $\hat {W}$
admits a Lefschetz fibration
$\hat {W}$
admits a Lefschetz fibration
![]() $\pi : \hat {W} \to \mathbb {C}$
by [Reference Giroux and Pardon28]. Then,
$\pi : \hat {W} \to \mathbb {C}$
by [Reference Giroux and Pardon28]. Then,
![]() $\pi $
defines a Fukaya-Seidel category. Moreover, it is known by [Reference Ganatra, Pardon and Shende29] that the corresponding Fukaya–Seidel category is the partially wrapped Fukaya category with the stop
$\pi $
defines a Fukaya-Seidel category. Moreover, it is known by [Reference Ganatra, Pardon and Shende29] that the corresponding Fukaya–Seidel category is the partially wrapped Fukaya category with the stop
![]() $\Lambda = \pi ^{-1}(-\infty )$
. Also, it is known that the Lefschetz thimbles of
$\Lambda = \pi ^{-1}(-\infty )$
. Also, it is known that the Lefschetz thimbles of
![]() $\pi $
generate
$\pi $
generate
![]() $\mathcal {W}(W, \Lambda )$
. Let G denote the generating Lagrangian submanifold.
$\mathcal {W}(W, \Lambda )$
. Let G denote the generating Lagrangian submanifold.
We note that wrapping a Lagrangian G means taking a time-t flow of a Hamiltonian vector field
![]() $X_H$
for positive time t, where
$X_H$
for positive time t, where
![]() $H: \hat {W} = W \cup ([1, \infty ] \times \partial W) \to \mathbb {R}$
is a Hamiltonian function satisfying the following:
$H: \hat {W} = W \cup ([1, \infty ] \times \partial W) \to \mathbb {R}$
is a Hamiltonian function satisfying the following:
 $$\begin{align*}H(x) = \begin{cases} 0 \text{ if } x \in W, \\ r \text{ if } x = (r, p) \in [1+\epsilon_0,\infty] \times \partial W \text{ with } 0 < \epsilon_0 \ll 1. \end{cases} \end{align*}$$
$$\begin{align*}H(x) = \begin{cases} 0 \text{ if } x \in W, \\ r \text{ if } x = (r, p) \in [1+\epsilon_0,\infty] \times \partial W \text{ with } 0 < \epsilon_0 \ll 1. \end{cases} \end{align*}$$
Since
![]() $\mathcal {W}(W,\Lambda )$
is fully stopped, there exists a positive number
$\mathcal {W}(W,\Lambda )$
is fully stopped, there exists a positive number
![]() $t_0$
such that the time-
$t_0$
such that the time-
![]() $t_0$
flow of
$t_0$
flow of
![]() $X_H$
, denoted by
$X_H$
, denoted by
![]() $\varphi _0$
, satisfies that
$\varphi _0$
, satisfies that
-
(A)
 $\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
$\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
 $n \in \mathbb {N}$
, and
$n \in \mathbb {N}$
, and -
(B)
 $HW_\Lambda \left (G,\phi ^n(G)\right ) = HF\left (\varphi _0(G),\phi ^n(G)\right )$
for all
$HW_\Lambda \left (G,\phi ^n(G)\right ) = HF\left (\varphi _0(G),\phi ^n(G)\right )$
for all
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
See Figure 1.

Figure 1 The interior of the black dotted circle is the base of a Lefschetz fibration
![]() $\pi $
. The star marked points are the singular values and the black dot is
$\pi $
. The star marked points are the singular values and the black dot is
![]() $-\infty $
. We note that the stop
$-\infty $
. We note that the stop
![]() $\Lambda $
is given by
$\Lambda $
is given by
![]() $\Lambda = \pi ^{-1}(-\infty )$
. One can choose G such that
$\Lambda = \pi ^{-1}(-\infty )$
. One can choose G such that
![]() $\pi (G)$
is the union of all black curves. Similarly,
$\pi (G)$
is the union of all black curves. Similarly,
![]() $\pi \left (\varphi _0(G)\right )$
is the union of all red curves. Let
$\pi \left (\varphi _0(G)\right )$
is the union of all red curves. Let
![]() $\pi (W)$
be contained in the interior of blue dotted circle. Then,
$\pi (W)$
be contained in the interior of blue dotted circle. Then,
![]() $\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
$\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
![]() $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
For a given
![]() $n \in \mathbb {N}$
, we apply Lemma 3.2 for the good pair of Lagrangians
$n \in \mathbb {N}$
, we apply Lemma 3.2 for the good pair of Lagrangians
![]() $\left (\varphi _0(G),\phi ^n(G)\right )$
. Then, there exists a family of Lagrangian
$\left (\varphi _0(G),\phi ^n(G)\right )$
. Then, there exists a family of Lagrangian
![]() $\{L^s\}_{s \in B^d_\epsilon }$
such that
$\{L^s\}_{s \in B^d_\epsilon }$
such that
-
(i)
 $\varphi _0(G)$
and
$\varphi _0(G)$
and
 $L^s$
are Hamiltonian isotopic to each other for all
$L^s$
are Hamiltonian isotopic to each other for all
 $s \in B_\epsilon ^d$
,
$s \in B_\epsilon ^d$
, -
(ii)
 $d_H(\varphi _0(G), L^s) < \frac {\epsilon }{2}$
, and
$d_H(\varphi _0(G), L^s) < \frac {\epsilon }{2}$
, and -
(iii)
 $L^s \pitchfork \phi ^n(G)$
for almost all
$L^s \pitchfork \phi ^n(G)$
for almost all
 $s \in B_\epsilon ^d$
.
$s \in B_\epsilon ^d$
.
We note that one can find a family
![]() $\{L^s\}_{s \in B^d_\epsilon }$
which does not depend on n. To be more precise, we remark that in the proof of Lemma 3.2, the construction of
$\{L^s\}_{s \in B^d_\epsilon }$
which does not depend on n. To be more precise, we remark that in the proof of Lemma 3.2, the construction of
![]() $\{L^s\}_{s \in B^d_\epsilon }$
depends only on
$\{L^s\}_{s \in B^d_\epsilon }$
depends only on
![]() $\epsilon $
, a collection of functions
$\epsilon $
, a collection of functions
![]() $\{g_1, \dots , g_d\}$
, and
$\{g_1, \dots , g_d\}$
, and
![]() $\ell $
in Equation (3.2). Since
$\ell $
in Equation (3.2). Since
![]() $\epsilon $
is a fixed, sufficiently small positive number,
$\epsilon $
is a fixed, sufficiently small positive number,
![]() $\epsilon $
is independent of n. Similarly,
$\epsilon $
is independent of n. Similarly,
![]() $\{g_1, \ldots , g_d\}$
is a collection of functions not depending on n.
$\{g_1, \ldots , g_d\}$
is a collection of functions not depending on n.
We recall that in order to define the value
![]() $\ell $
in Equation (3.2), we had to fix
$\ell $
in Equation (3.2), we had to fix
![]() $W_0 \subset W$
such that
$W_0 \subset W$
such that
Without loss of generality, one can assume that
![]() $W_0$
not only satisfies the above two conditions, but also contains the support of
$W_0$
not only satisfies the above two conditions, but also contains the support of
![]() $\phi $
. Then, outside of
$\phi $
. Then, outside of
![]() $W_0$
,
$W_0$
,
![]() $\phi ^{n_1}(G)$
and
$\phi ^{n_1}(G)$
and
![]() $\phi ^{n_2}(G)$
agree for all
$\phi ^{n_2}(G)$
agree for all
![]() $n_i \in \mathbb {N}$
. Thus,
$n_i \in \mathbb {N}$
. Thus,
![]() $\ell $
in Equation (3.2) does not depend on n.
$\ell $
in Equation (3.2) does not depend on n.
Since we have a family
![]() $\{L^s\}_{s \in B^d_\epsilon }$
not depending on n, one can define the following function
$\{L^s\}_{s \in B^d_\epsilon }$
not depending on n, one can define the following function
We point out that for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $N_n(s)$
is an integrable function because of (iii).
$N_n(s)$
is an integrable function because of (iii).
By applying Lemma 3.4, we have
 $$ \begin{align} \int_{B^d_\epsilon} N_n(s) ds \leq C \cdot \mathrm{Vol}\left(\phi^n(G) \cap W\right). \end{align} $$
$$ \begin{align} \int_{B^d_\epsilon} N_n(s) ds \leq C \cdot \mathrm{Vol}\left(\phi^n(G) \cap W\right). \end{align} $$
We note that the constant C in (4.1) is independent of n.
On the other hand, for
![]() $s \in B_{\epsilon }^d$
such that
$s \in B_{\epsilon }^d$
such that
![]() $L^s$
and
$L^s$
and
![]() $ \phi ^n(G)$
intersect transversely, we have
$ \phi ^n(G)$
intersect transversely, we have
The first equality holds because of (B), the second equality holds because of (i), and the last inequality holds because of the definition of Lagrangian Floer homology.
Since (4.2) holds for almost every
![]() $s\in B_{\epsilon }^d$
, by integrating Equation (4.2), we have
$s\in B_{\epsilon }^d$
, by integrating Equation (4.2), we have
 $$ \begin{align} \mathrm{Vol}(B^d_\epsilon) \cdot \mathrm{dim}HW_\Lambda\left(G,\phi^n(G)\right) = \int_{B^d_\epsilon} \mathrm{dim}HW_\Lambda\left(G,\phi^n(G)\right) ds \leq \int_{B^d_\epsilon} N_n(s) ds. \end{align} $$
$$ \begin{align} \mathrm{Vol}(B^d_\epsilon) \cdot \mathrm{dim}HW_\Lambda\left(G,\phi^n(G)\right) = \int_{B^d_\epsilon} \mathrm{dim}HW_\Lambda\left(G,\phi^n(G)\right) ds \leq \int_{B^d_\epsilon} N_n(s) ds. \end{align} $$
From two inequalities (4.1) and (4.3), one has
By taking
![]() $\limsup _{n \to \infty } \frac {1}{n} \log ^+$
for the both hand sides of (4.4), one has
$\limsup _{n \to \infty } \frac {1}{n} \log ^+$
for the both hand sides of (4.4), one has
 $$ \begin{align} h_{cat}\left(\Phi_\Lambda : \mathcal{W}(W,\Lambda) \to \mathcal{W}(W,\Lambda)\right) &= \limsup_{n\to\infty} \frac{1}{n} \log \dim HW_\Lambda\left(\varphi_0(G),\phi^n(G)\right) \\ \notag &\leq \limsup_{n \to \infty} \frac{1}{n} \log \mathrm{Vol}\left(\phi^n(G) \cap W\right). \end{align} $$
$$ \begin{align} h_{cat}\left(\Phi_\Lambda : \mathcal{W}(W,\Lambda) \to \mathcal{W}(W,\Lambda)\right) &= \limsup_{n\to\infty} \frac{1}{n} \log \dim HW_\Lambda\left(\varphi_0(G),\phi^n(G)\right) \\ \notag &\leq \limsup_{n \to \infty} \frac{1}{n} \log \mathrm{Vol}\left(\phi^n(G) \cap W\right). \end{align} $$
The first equality in Equation (4.5) holds because of [Reference Dimitrov, Haiden, Katzarkov and Kontsevich18, Theorem 2.6] and because
![]() $\mathcal {W}(W, \Lambda )$
is smooth and proper.
$\mathcal {W}(W, \Lambda )$
is smooth and proper.
Lemma 2.10 says that
Also the following holds by Theorem 2.5,
Remark 4.2.
-
1. In the proof of Theorem 4.1, we fix a Lefschetz fibration, and we use the corresponding Fukaya-Seidel category. We note that if one fixes a fully stopped partially wrapped Fukaya category instead of a Fukaya–Seidel category, the same proof still works.
-
2. A direct application of Theorem 4.1 is to show that the topological entropy of some symplectic automorphisms are positive. For example, [Reference Gong, Wang and Xue31, Theorem 1.2] shows that symplectic automorphisms of a specific type, defined on the Milnor fibers of
 $A_n$
-type, admit positive topological entropy. For the symplectic automorphisms which [Reference Gong, Wang and Xue31] considers, one can check that their categorical entropy are positive by [Reference Bae, Choa, Jeong, Karabas and Lee9, Theorem 7.14 and Lemma 8.5]. Then, Theorem 4.1 guarantees that the topological entropy is also positive. We note that [Reference Gong, Wang and Xue31] shows their result by showing that the symplectic automorphisms have certain form of nonuniform hyperbolicity.
$A_n$
-type, admit positive topological entropy. For the symplectic automorphisms which [Reference Gong, Wang and Xue31] considers, one can check that their categorical entropy are positive by [Reference Bae, Choa, Jeong, Karabas and Lee9, Theorem 7.14 and Lemma 8.5]. Then, Theorem 4.1 guarantees that the topological entropy is also positive. We note that [Reference Gong, Wang and Xue31] shows their result by showing that the symplectic automorphisms have certain form of nonuniform hyperbolicity.
5 Examples
In this section, we provide two examples. The first example is a symplectic automorphism for which the inequality (1.1) is strict. The second example shows that categorical entropy can be strictly greater than the spectral radius of its induced map on the homology.
5.1 The first example
Let W be a 2-dimensional Weinstein domain such that
![]() $W \neq \mathbb {D}^2$
. It is well-known that its wrapped Fukaya category is generated by the Lagrangian cocores, see [Reference Chantraine, Rizell, Ghiggini and Golovko14], [Reference Ganatra, Pardon and Shende29]. This ensures that the categorical entropy of an endo-functor on
$W \neq \mathbb {D}^2$
. It is well-known that its wrapped Fukaya category is generated by the Lagrangian cocores, see [Reference Chantraine, Rizell, Ghiggini and Golovko14], [Reference Ganatra, Pardon and Shende29]. This ensures that the categorical entropy of an endo-functor on
![]() $\mathcal {W}(W)$
is well-defined.
$\mathcal {W}(W)$
is well-defined.
Let U be a small open ball in W. It is well-known that there is a Hamiltonian diffeomorphism
![]() $\widetilde {\phi }: \overline {U} \to \overline {U}$
defined on the closure of U such that
$\widetilde {\phi }: \overline {U} \to \overline {U}$
defined on the closure of U such that
-
•
 $\tilde {\phi }$
is the identity near the boundary of
$\tilde {\phi }$
is the identity near the boundary of
 $\overline {U}$
, and
$\overline {U}$
, and -
•
 $\tilde {\phi }$
has a positive topological entropy.
$\tilde {\phi }$
has a positive topological entropy.
Smale’s horseshoe map is an example of such
![]() $\tilde {\phi }$
.
$\tilde {\phi }$
.
Since
![]() $\widetilde {\phi }$
is assumed to be the identity near the boundary of the closure of U, it admits a trivial extension to the whole Weinstein domain W, which we will call
$\widetilde {\phi }$
is assumed to be the identity near the boundary of the closure of U, it admits a trivial extension to the whole Weinstein domain W, which we will call
![]() $\phi $
. Since
$\phi $
. Since
![]() $\phi $
is a compactly supported Hamiltonian diffeomorphism, if we let
$\phi $
is a compactly supported Hamiltonian diffeomorphism, if we let
![]() $\Phi $
be its induced functor on
$\Phi $
be its induced functor on
![]() $\mathcal {W}(W)$
as above, then we have
$\mathcal {W}(W)$
as above, then we have
Hence
![]() $\phi $
is an example showing that the inequality (1.1) can be strict.
$\phi $
is an example showing that the inequality (1.1) can be strict.
5.2 The second example
Let
![]() $\phi :\hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism of a Weinstein manifold
$\phi :\hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism of a Weinstein manifold
![]() $\hat {W}$
. Let
$\hat {W}$
. Let
![]() $\phi _*: H_*(\hat {W}) \to H_*(\hat {W})$
be the linear map on the homology of
$\phi _*: H_*(\hat {W}) \to H_*(\hat {W})$
be the linear map on the homology of
![]() $\hat {W}$
that
$\hat {W}$
that
![]() $\phi $
induces. We define the spectral radius of
$\phi $
induces. We define the spectral radius of
![]() $\phi $
as the maximal absolute value of eigenvalues of
$\phi $
as the maximal absolute value of eigenvalues of
![]() $\phi _*$
. Let
$\phi _*$
. Let
![]() $\mathrm {Rad}(\phi )$
denote the spectral radius of
$\mathrm {Rad}(\phi )$
denote the spectral radius of
![]() $\phi $
. It is a well-known fact due to Yomdin [Reference Yomdin50] that logarithm
$\phi $
. It is a well-known fact due to Yomdin [Reference Yomdin50] that logarithm
![]() $\log \mathrm {Rad}(\phi )$
of the spectral radius is a lower bound of
$\log \mathrm {Rad}(\phi )$
of the spectral radius is a lower bound of
![]() $h_{top}(\phi )$
. We refer the reader to [Reference Gromov30], [Reference Yomdin50] for more details. Since Theorem 4.1 gives another lower bound of
$h_{top}(\phi )$
. We refer the reader to [Reference Gromov30], [Reference Yomdin50] for more details. Since Theorem 4.1 gives another lower bound of
![]() $h_{top}(\phi )$
, that is,
$h_{top}(\phi )$
, that is,
![]() $h_{cat}(\Phi )$
, one can ask the relationship between two lower bounds of
$h_{cat}(\Phi )$
, one can ask the relationship between two lower bounds of
![]() $h_{top}(\phi )$
. In this subsection, first, we give an example of
$h_{top}(\phi )$
. In this subsection, first, we give an example of
![]() $\phi $
such that
$\phi $
such that
The example shows that the categorical entropy could be an useful tool for proving positivity of topological entropy of symplectomorphisms. After introducing the example, we also introduce a construction of symplectomorphisms having positive topological entropy.
To introduce the example, let A and B be n-dimensional spheres. Then let
![]() $\hat {W}$
be the plumbing of the cotangent bundles
$\hat {W}$
be the plumbing of the cotangent bundles
![]() $T^*A$
and
$T^*A$
and
![]() $T^*B$
at a point. In other words,
$T^*B$
at a point. In other words,
![]() $\hat {W}$
is the Milnor fiber of
$\hat {W}$
is the Milnor fiber of
![]() $A_2$
-type.
$A_2$
-type.
Let
![]() $\tau _A$
and
$\tau _A$
and
![]() $\tau _B$
be the Dehn twist defined on W along A and B, respectively. Let us consider the symplectic automorphism on
$\tau _B$
be the Dehn twist defined on W along A and B, respectively. Let us consider the symplectic automorphism on
![]() $\hat {W}$
given by
$\hat {W}$
given by
Now observe that the homology of
![]() $\hat {W}$
is given by
$\hat {W}$
is given by
 $$\begin{align*}H_*(\hat{W}) = \begin{cases} \mathbb{Z} \langle [pt] \rangle &*=0, \\ \mathbb{Z} \langle [A], [B]\rangle & *=n,\\ 0 &\text{otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}H_*(\hat{W}) = \begin{cases} \mathbb{Z} \langle [pt] \rangle &*=0, \\ \mathbb{Z} \langle [A], [B]\rangle & *=n,\\ 0 &\text{otherwise.} \end{cases}\end{align*}$$
Since
![]() $\phi $
induces the trivial map on the zeroth homology
$\phi $
induces the trivial map on the zeroth homology
![]() $H_0(\hat {W})$
, it is enough to consider its induced map on the n-dimensional homology
$H_0(\hat {W})$
, it is enough to consider its induced map on the n-dimensional homology
![]() $H_n(\hat {W})$
to compute
$H_n(\hat {W})$
to compute
![]() $\mathrm {Rad}(\phi _*)$
.
$\mathrm {Rad}(\phi _*)$
.
For that purpose, we consider the induced map of
![]() $\tau _A$
and
$\tau _A$
and
![]() $\tau _B$
on
$\tau _B$
on
![]() $H_n(\hat {W})$
separately.
$H_n(\hat {W})$
separately.
-
1.
 $(\tau _A)_*([A]) = (-1)^{n-1}[A]$
.
$(\tau _A)_*([A]) = (-1)^{n-1}[A]$
. -
2.
 $(\tau _A)_*([B]) = [A]+[B]$
.
$(\tau _A)_*([B]) = [A]+[B]$
. -
3.
 $(\tau _B)_*([A]) = [A] +(-1)^n [B]$
.
$(\tau _B)_*([A]) = [A] +(-1)^n [B]$
. -
4.
 $(\tau _B)_*([B]) = (-1)^{n-1}[B]$
.
$(\tau _B)_*([B]) = (-1)^{n-1}[B]$
.
In other words,
![]() $(\tau _A)_*$
and
$(\tau _A)_*$
and
![]() $(\tau _B)_*$
are represented by the matrices
$(\tau _B)_*$
are represented by the matrices
 $$\begin{align*}(\tau_A)_* = \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1\end{pmatrix} \text{ and } (\tau_B)_* = \begin{pmatrix} 1& 0 \\ (-1)^n & (-1)^{n-1}\end{pmatrix}, \end{align*}$$
$$\begin{align*}(\tau_A)_* = \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1\end{pmatrix} \text{ and } (\tau_B)_* = \begin{pmatrix} 1& 0 \\ (-1)^n & (-1)^{n-1}\end{pmatrix}, \end{align*}$$
respectively.
Consequently, the map
![]() $\phi _* = (\tau _A)_* \circ (\tau _B^{-1})_*$
is represented by
$\phi _* = (\tau _A)_* \circ (\tau _B^{-1})_*$
is represented by
 $$ \begin{align*} \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1& 0 \\ (-1)^n & (-1)^{n-1}\end{pmatrix}^{-1} &= \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1& 0 \\ 1 & (-1)^{n-1}\end{pmatrix}\\ &= \begin{pmatrix}1+(-1)^{n-1}& (-1)^{n-1}\\ 1 & (-1)^{n-1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1& 0 \\ (-1)^n & (-1)^{n-1}\end{pmatrix}^{-1} &= \begin{pmatrix} (-1)^{n-1} & 1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1& 0 \\ 1 & (-1)^{n-1}\end{pmatrix}\\ &= \begin{pmatrix}1+(-1)^{n-1}& (-1)^{n-1}\\ 1 & (-1)^{n-1} \end{pmatrix}. \end{align*} $$
Let us now assume that n is even. Then the above matrix is
 $$\begin{align*}\begin{pmatrix} 0 & -1\\ 1 & -1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0 & -1\\ 1 & -1 \end{pmatrix}. \end{align*}$$
A straightforward computation shows that its eigenvalues are
 $$\begin{align*}\frac{-1 + \sqrt{3} i}{2} \text{ and } \frac{-1- \sqrt{3}i}{2}.\end{align*}$$
$$\begin{align*}\frac{-1 + \sqrt{3} i}{2} \text{ and } \frac{-1- \sqrt{3}i}{2}.\end{align*}$$
Hence the spectral radius of
![]() $\phi _*$
is
$\phi _*$
is
 $$\begin{align*}\left|\frac{-1+\sqrt{3}i}{2} \right| = \left|\frac{-1- \sqrt{3}i}{2} \right| =1.\end{align*}$$
$$\begin{align*}\left|\frac{-1+\sqrt{3}i}{2} \right| = \left|\frac{-1- \sqrt{3}i}{2} \right| =1.\end{align*}$$
On the other hand, [Reference Bae and Lee10, Theorem 1.5] says that the categorical entropy of the induced map of
![]() $\phi $
on the wrapped Fukaya category is the same as its stretching factor. Moreover, one can easily compute the stretching factor of
$\phi $
on the wrapped Fukaya category is the same as its stretching factor. Moreover, one can easily compute the stretching factor of
![]() $\phi $
by employing the techniques in [Reference Bae and Lee10], and the stretching factor of the given example
$\phi $
by employing the techniques in [Reference Bae and Lee10], and the stretching factor of the given example
![]() $\phi $
is
$\phi $
is
 $$\begin{align*}\frac{3+\sqrt{5}}{2}.\end{align*}$$
$$\begin{align*}\frac{3+\sqrt{5}}{2}.\end{align*}$$
We note that the detailed computation could be found in [Reference Bae and Lee10, Section 11.1].
Finally, we can prove that
![]() $\phi $
has positive topological entropy even though the spectral radius of
$\phi $
has positive topological entropy even though the spectral radius of
![]() $\phi $
is
$\phi $
is
![]() $1$
, since
$1$
, since
 $$\begin{align*}\log \mathrm{Rad}( \phi) =0 <\frac{3+\sqrt{5}}{2} = h_{cat} (\Phi) \leq h_{top}(\phi).\end{align*}$$
$$\begin{align*}\log \mathrm{Rad}( \phi) =0 <\frac{3+\sqrt{5}}{2} = h_{cat} (\Phi) \leq h_{top}(\phi).\end{align*}$$
We would like to note that the above example
![]() $\phi $
is a symplectic automorphism constructed by a construction introduced in [Reference Lee37]. We introduce the construction given in [Reference Lee37] and prove that if a symplectic automorphism
$\phi $
is a symplectic automorphism constructed by a construction introduced in [Reference Lee37]. We introduce the construction given in [Reference Lee37] and prove that if a symplectic automorphism
![]() $\psi $
is compactly supported Hamiltonian isotopic to any symplectic automorphism
$\psi $
is compactly supported Hamiltonian isotopic to any symplectic automorphism
![]() $\phi $
constructed in [Reference Lee37], then
$\phi $
constructed in [Reference Lee37], then
![]() $\psi $
has positive topological entropy.
$\psi $
has positive topological entropy.
The following is the construction given in [Reference Lee37] with a technical condition.
Definition 5.1. Let M be a symplectic manifold and
![]() $\phi :M \to M$
be a symplectic automorphism. We call that
$\phi :M \to M$
be a symplectic automorphism. We call that
![]() $\phi $
is of Penner type if there exist two collections of Lagrangian spheres in M,
$\phi $
is of Penner type if there exist two collections of Lagrangian spheres in M,
satisfying the following conditions:
-
(i)
 $\phi $
is a product of positive powers of
$\phi $
is a product of positive powers of
 $\tau _i$
and negative powers of
$\tau _i$
and negative powers of
 $\sigma _j$
where
$\sigma _j$
where
 $\tau _i$
and
$\tau _i$
and
 $\sigma _j$
are generalized Dehn twists along
$\sigma _j$
are generalized Dehn twists along
 $\alpha _i$
and
$\alpha _i$
and
 $\beta _j$
, respectively.
$\beta _j$
, respectively. -
(ii)
 $\{\alpha _1, \dots , \alpha _s\}$
and
$\{\alpha _1, \dots , \alpha _s\}$
and
 $\{\beta _1, \dots , \beta _t\}$
are pair-wisely disjoint collections of Lagrangian spheres and
$\{\beta _1, \dots , \beta _t\}$
are pair-wisely disjoint collections of Lagrangian spheres and
 $\alpha _i$
and
$\alpha _i$
and
 $\beta _j$
are transverse to each other.
$\beta _j$
are transverse to each other. -
(iii) Let G be a graph such that
-
• whose vertex set is
 $\{\alpha _1, \dots , \alpha _s, \beta _1, \dots , \beta _t\}$
and
$\{\alpha _1, \dots , \alpha _s, \beta _1, \dots , \beta _t\}$
and -
• two vertices
 $v, w \in \{\alpha _1, \dots , \alpha _s, \beta _1, \dots , \beta _t\}$
are connected by k edges if the number of intersection points of two Lagrangian spheres is k, that is,
$v, w \in \{\alpha _1, \dots , \alpha _s, \beta _1, \dots , \beta _t\}$
are connected by k edges if the number of intersection points of two Lagrangian spheres is k, that is,
 $|v \cap w| =k$
.
$|v \cap w| =k$
.
Then, the graph G is a tree.
-
Remark 5.2. We remark that Definition 5.1 is motivated from Penner’s construction of pseudo-Anosov surface mapping classes, introduced in [Reference Penner41]. One can easily see that two conditions (i) and (ii) of Definition 5.1 are generalizations of the original construction of Penner. The third condition (iii) is a technical condition which we need, in order to employ the result of [Reference Bae and Lee10]. However, we expect that the technical condition could be removed. More details will be mentioned in Remark 5.4.
Now, we prove the main result of the present subsection.
Theorem 5.3. Let M be a symplectic manifold of dimension
![]() $\geq 6$
. If a symplectic automorphism
$\geq 6$
. If a symplectic automorphism
![]() $\phi :M \to M$
is of Penner type, then
$\phi :M \to M$
is of Penner type, then
Proof. We note that any Penner type
![]() $\phi $
is compactly supported by Definition 5.1. Moreover, the compact support of
$\phi $
is compactly supported by Definition 5.1. Moreover, the compact support of
![]() $\phi $
is given as a small neighborhood of
$\phi $
is given as a small neighborhood of
Thanks to Weinstein’s neighborhood theorem [Reference Weinstein49], we could assume that the compact support is a subset of a plumbing space P of
![]() $T^*S^n$
where n is the dimension of the Lagrangian spheres. Moreover, the plumbing pattern of P is determined by the intersection pattern of
$T^*S^n$
where n is the dimension of the Lagrangian spheres. Moreover, the plumbing pattern of P is determined by the intersection pattern of
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _j$
. Thus, the plumbing pattern is the graph G defined in 5.1 (iii).
$\beta _j$
. Thus, the plumbing pattern is the graph G defined in 5.1 (iii).
Simply, we have
Now, we can consider a symplectic automorphism
![]() $\phi _0: P \to P$
, which is a natural extension of the restriction of
$\phi _0: P \to P$
, which is a natural extension of the restriction of
![]() $\phi $
on the compact support. Then, we have that the topological entropy of
$\phi $
on the compact support. Then, we have that the topological entropy of
![]() $\phi $
and
$\phi $
and
![]() $\phi _0$
coincide. Thus, it is enough to show that
$\phi _0$
coincide. Thus, it is enough to show that
![]() $h_{cat}(\Phi _0)>0$
.
$h_{cat}(\Phi _0)>0$
.
Note that the domain of
![]() $\phi _0$
is a plumbing space P whose plumbing pattern is a tree. Thus, we can employ the results of [Reference Bae and Lee10]. Finally, [Reference Bae and Lee10, Theorems 1.5 and 7.1] proves that
$\phi _0$
is a plumbing space P whose plumbing pattern is a tree. Thus, we can employ the results of [Reference Bae and Lee10]. Finally, [Reference Bae and Lee10, Theorems 1.5 and 7.1] proves that
![]() $h_{cat}(\Phi _0)>0$
.
$h_{cat}(\Phi _0)>0$
.
Remark 5.4. We end this subsection with remarks on Theorem 5.3 and Definition 5.1 (iii).
-
1. We note that the proof of Theorem 5.3 used the results in [Reference Bae and Lee10] without details. We want to simply explain the idea of [Reference Bae and Lee10] before moving on to the next section. The main result of [Reference Bae and Lee10] is to show that if
 $\phi $
is of Penner type, then
$\phi $
is of Penner type, then
 $\phi $
induces a functor on Fukaya category having simple asymptotic behavior. In other words,
$\phi $
induces a functor on Fukaya category having simple asymptotic behavior. In other words,
 $\Phi ^n$
has a simple, in a categorical sense, behavior as
$\Phi ^n$
has a simple, in a categorical sense, behavior as
 $n \to \infty $
. It is expected by [Reference Lee37] that shows a simple, in a geometric sense, asymptotic behavior of
$n \to \infty $
. It is expected by [Reference Lee37] that shows a simple, in a geometric sense, asymptotic behavior of
 $\phi $
. To prove the simple asymptotic behaviors of Penner type symplectic automorphisms, [Reference Bae and Lee10], [Reference Lee37] generalized the notion of measured train track and linear algebras on it in geometric and categorical senses. For more details on measured train tracks, we refer the reader to [Reference Farb and Margalit24]
$\phi $
. To prove the simple asymptotic behaviors of Penner type symplectic automorphisms, [Reference Bae and Lee10], [Reference Lee37] generalized the notion of measured train track and linear algebras on it in geometric and categorical senses. For more details on measured train tracks, we refer the reader to [Reference Farb and Margalit24] -
2. As mentioned in Remark 5.2, Definition 5.1 (iii) is a technical condition. We note that thanks to the technical condition, we can guarantee that the plumbing pattern of P in the proof of Theorem 5.3 is a tree. Then, since there exist known generators of the compact Fukaya category of P, we can employ the techniques in [Reference Bae and Lee10].
However, we expect that one can choose specific generators of compact Fukaya category of any plumbing space. This is an ongoing project of the second-named author, together with Wonbo Jeong and Dogancan Karabas. After fixing generators of compact Fukaya category of a general plumbing space, we expect that the result of [Reference Bae and Lee10] could be generalized on a general plumbing space. And, it allows us to drop the technical condition, that is, Definition 5.1 (iii).
6 The case of compact Fukaya category
As mentioned in the introduction, we prove that a variant of Theorem 4.1 holds for compact Fukaya category under an additional assumption. Let
![]() $(\hat {W},d\lambda )$
be a Weinstein manifold and let
$(\hat {W},d\lambda )$
be a Weinstein manifold and let
![]() $W\subset \hat {W}$
be an associated Weinstein domain. The assumption we consider is a kind of “duality” between compact and wrapped Fukaya categories of W. We start Section 6 by giving a specific example satisfying the “duality”.
$W\subset \hat {W}$
be an associated Weinstein domain. The assumption we consider is a kind of “duality” between compact and wrapped Fukaya categories of W. We start Section 6 by giving a specific example satisfying the “duality”.
Let T be a tree and let
![]() $P_n(T)$
be the plumbing of the cotangent bundles of
$P_n(T)$
be the plumbing of the cotangent bundles of
![]() $T^*S^n$
along T as in [Reference Bae, Choa, Jeong, Karabas and Lee9]. For each vertex v of T, let
$T^*S^n$
along T as in [Reference Bae, Choa, Jeong, Karabas and Lee9]. For each vertex v of T, let
![]() $S_v$
be the Lagrangian sphere in
$S_v$
be the Lagrangian sphere in
![]() $P_n(T)$
corresponding to v, and let
$P_n(T)$
corresponding to v, and let
![]() $L_v$
be the Lagrangian cocore disk corresponding to v. This means that the Lagrangian spheres
$L_v$
be the Lagrangian cocore disk corresponding to v. This means that the Lagrangian spheres
![]() $S_v$
and the Lagrangian cocore disks
$S_v$
and the Lagrangian cocore disks
![]() $L_v$
intersect transversely and that the intersection numbers between those are given by
$L_v$
intersect transversely and that the intersection numbers between those are given by
 $$\begin{align*}|S_v \cap L_w| =\begin{cases} 1 & v= w,\\ 0 &\text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}|S_v \cap L_w| =\begin{cases} 1 & v= w,\\ 0 &\text{ otherwise.} \end{cases} \end{align*}$$
We note that [Reference Bae, Choa, Jeong, Karabas and Lee9] compares the categorical entropies on compact and wrapped Fukaya categories of
![]() $P_n(T)$
by using [Reference Abouzaid and Smith8, Lemma 2.5] and the above Lagrangians
$P_n(T)$
by using [Reference Abouzaid and Smith8, Lemma 2.5] and the above Lagrangians
![]() $\{S_v\}$
and
$\{S_v\}$
and
![]() $\{L_v\}$
. Motivated by this, we will assume the following in this subsection.
$\{L_v\}$
. Motivated by this, we will assume the following in this subsection.
Assumptions 6.1. There exists a finite collection of exact, closed Lagrangians
![]() $\{S_i\}_{i \in I}$
of
$\{S_i\}_{i \in I}$
of
![]() $\hat {W}$
indexed by some set I such that
$\hat {W}$
indexed by some set I such that
-
1. the direct sum
 $S = \oplus _{i \in I} S_v$
split-generates the compact Fukaya category
$S = \oplus _{i \in I} S_v$
split-generates the compact Fukaya category
 $\mathcal {F}(W)$
in such way that every exact, closed Lagrangian L of
$\mathcal {F}(W)$
in such way that every exact, closed Lagrangian L of
 $\hat {W}$
is quasi-isomorphic to a twisted complex for L with components
$\hat {W}$
is quasi-isomorphic to a twisted complex for L with components
 $\{S_i\}$
, in which none of the arrows are nonzero multiples of the identity morphisms, and
$\{S_i\}$
, in which none of the arrows are nonzero multiples of the identity morphisms, and -
2. there exists another collection of Lagrangians
 $\{L_i\}_{i \in I}$
of
$\{L_i\}_{i \in I}$
of
 $\hat {W}$
, each of which intersects
$\hat {W}$
, each of which intersects
 $S_i \in I$
transversely and satisfies
$S_i \in I$
transversely and satisfies  $$\begin{align*}|S_i \cap L_j| =\begin{cases} 1 & i= j,\\ 0 &\text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}|S_i \cap L_j| =\begin{cases} 1 & i= j,\\ 0 &\text{ otherwise.} \end{cases} \end{align*}$$
Let
![]() $S = \bigoplus _{i \in I} S_i$
and
$S = \bigoplus _{i \in I} S_i$
and
![]() $L = \bigoplus _{i \in I} L_i$
. Let us denote by
$L = \bigoplus _{i \in I} L_i$
. Let us denote by
![]() $\Phi _{\mathcal {F}(W)}$
the auto-functor on
$\Phi _{\mathcal {F}(W)}$
the auto-functor on
![]() $\mathcal {F}(W)$
induced by
$\mathcal {F}(W)$
induced by
![]() $\phi $
. Then, since the arguments in [Reference Bae, Choa, Jeong, Karabas and Lee9, Lemma 6.5 and Theorem 6.6] continue to work under Assumption 6.1, we have Lemma 6.2.
$\phi $
. Then, since the arguments in [Reference Bae, Choa, Jeong, Karabas and Lee9, Lemma 6.5 and Theorem 6.6] continue to work under Assumption 6.1, we have Lemma 6.2.
Lemma 6.2. For any exact, compactly-supported symplectic automorphism
![]() $\phi $
on a Weinstein manifold
$\phi $
on a Weinstein manifold
![]() $\hat {W}$
, if
$\hat {W}$
, if
![]() $\hat {W}$
satisfies Assumption 6.1, then
$\hat {W}$
satisfies Assumption 6.1, then
Theorem 6.3. Let a pair
![]() $(\hat {W},\phi : \hat {W} \to \hat {W})$
be as in Lemma 6.2. Then the categorical entropy
$(\hat {W},\phi : \hat {W} \to \hat {W})$
be as in Lemma 6.2. Then the categorical entropy
![]() $h_{cat}(\Phi _{\mathcal {F}(W)})$
for its induced functor on the compact Fukaya category
$h_{cat}(\Phi _{\mathcal {F}(W)})$
for its induced functor on the compact Fukaya category
![]() $\mathcal {F}(W)$
bounds the topological entropy of
$\mathcal {F}(W)$
bounds the topological entropy of
![]() $\phi $
from below, that is,
$\phi $
from below, that is,
Proof. Basically, most arguments in the proof of Theorem 4.1 can be applied to this case. Indeed, for
![]() $n \in \mathbb {N}$
, we once again apply Lemma 3.2 to the pair
$n \in \mathbb {N}$
, we once again apply Lemma 3.2 to the pair
![]() $( S, \phi ^{-n}(L) )$
to get a family of Lagrangians
$( S, \phi ^{-n}(L) )$
to get a family of Lagrangians
![]() $\{S^s\}_{s \in B_{\epsilon }^d}$
such that
$\{S^s\}_{s \in B_{\epsilon }^d}$
such that
-
(i) S and
 $S^s$
are Hamiltonian isotopic to each other for all
$S^s$
are Hamiltonian isotopic to each other for all
 $s \in B_\epsilon ^d$
,
$s \in B_\epsilon ^d$
, -
(ii)
 $d_H(S, S^s) < \frac {\epsilon }{2}$
, and
$d_H(S, S^s) < \frac {\epsilon }{2}$
, and -
(iii)
 $S^s \pitchfork \phi ^{-n}(L)$
for almost all
$S^s \pitchfork \phi ^{-n}(L)$
for almost all
 $s \in B_\epsilon ^d$
.
$s \in B_\epsilon ^d$
.
As mentioned in the proof of 4.1, one can find such a family
![]() $\{S^s\}_{s\in B_{\epsilon }^d}$
, for which the third condition (iii) holds for all
$\{S^s\}_{s\in B_{\epsilon }^d}$
, for which the third condition (iii) holds for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Then we consider the following function
By applying Lemma 3.4 once again, we have
 $$ \begin{align} \int_{B^d_\epsilon} N_n(s) ds \leq C' \cdot \mathrm{Vol}\left(\phi^{-n}(L) \cap W\right). \end{align} $$
$$ \begin{align} \int_{B^d_\epsilon} N_n(s) ds \leq C' \cdot \mathrm{Vol}\left(\phi^{-n}(L) \cap W\right). \end{align} $$
for some constant
![]() $C'$
which does not depend on n.
$C'$
which does not depend on n.
On the other hand, for
![]() $S^s \pitchfork \phi ^{-n}(L)$
, we have
$S^s \pitchfork \phi ^{-n}(L)$
, we have
The above inequality holds since S and
![]() $S^s$
are Hamiltonian isotopic.
$S^s$
are Hamiltonian isotopic.
By integrating Equation (6.2), one has
 $$ \begin{align} \mathrm{Vol}(B^d_\epsilon) \cdot \mathrm{dim}HF \left(\phi^n(S),L\right) = \int_{B^d_\epsilon} \mathrm{dim}HF \left(\phi^n(S),L\right) ds \leq \int_{B^d_\epsilon} N_n(s) ds. \end{align} $$
$$ \begin{align} \mathrm{Vol}(B^d_\epsilon) \cdot \mathrm{dim}HF \left(\phi^n(S),L\right) = \int_{B^d_\epsilon} \mathrm{dim}HF \left(\phi^n(S),L\right) ds \leq \int_{B^d_\epsilon} N_n(s) ds. \end{align} $$
From two inequalities (6.1) and (6.3), one has
By taking
![]() $\limsup _{n \to \infty } \frac {1}{n} \log $
for the both hand sides of (6.4) and using Lemma 6.2, one has
$\limsup _{n \to \infty } \frac {1}{n} \log $
for the both hand sides of (6.4) and using Lemma 6.2, one has
 $$ \begin{align} h_{cat} (\Phi_{\mathcal{F}(W)}) &= \limsup_{n\to\infty} \frac{1}{n} \log \dim HF \left(\phi^n(S),L\right) \\ \notag &\leq \limsup_{n \to \infty} \frac{1}{n} \log \mathrm{Vol}\left(\phi^{-n}(L) \cap W\right). \end{align} $$
$$ \begin{align} h_{cat} (\Phi_{\mathcal{F}(W)}) &= \limsup_{n\to\infty} \frac{1}{n} \log \dim HF \left(\phi^n(S),L\right) \\ \notag &\leq \limsup_{n \to \infty} \frac{1}{n} \log \mathrm{Vol}\left(\phi^{-n}(L) \cap W\right). \end{align} $$
Here the latter is again bounded above by
![]() $h_{top}(\phi )$
due to Theorem 2.5. Therefore, (6.5) proves the assertion.
$h_{top}(\phi )$
due to Theorem 2.5. Therefore, (6.5) proves the assertion.
7 Barcode entropy
In this section, we define another entropy, called barcode entropy. As mentioned in Section 1.2, the notion of barcode entropy is the same as the relative barcode entropy defined in [Reference Cineli, Ginzburg and Gürel13]. At the end of Section 7, we give further questions related to categorical, topological, and barcode entropies.
7.1 Preliminaries
In this subsection, we review the theory of persistence modules, and we apply it to Lagrangian Floer homology. We refer the reader to [Reference Polterovich, Rosen, Samvelyan and Zhang42], [Reference Usher and Zhang48] for the theory of persistence modules. Also, we refer the reader to [Reference Cineli, Ginzburg and Gürel13] for the details we omitted in the current subsection.
The notion of non-Archimedean norm on a vector space is defined in [Reference Usher and Zhang48, Definition 2.2]. It is easy to check that
![]() $\mathcal {A}$
in (2.2) is a non-Archimedean norm on the k-vector space
$\mathcal {A}$
in (2.2) is a non-Archimedean norm on the k-vector space
![]() $CF(L_1,L_2)$
. Moreover,
$CF(L_1,L_2)$
. Moreover,
![]() $CF(L_1,L_2)$
is orthogonal with respect to
$CF(L_1,L_2)$
is orthogonal with respect to
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Now, we are ready to apply [Reference Usher and Zhang48, Theorem 3.4] for the differential
Since
![]() $\delta $
is a linear self-mapping of an orthogonal vector space
$\delta $
is a linear self-mapping of an orthogonal vector space
![]() $CF(L_1,L_2)$
, one obtains a basis
$CF(L_1,L_2)$
, one obtains a basis
![]() $\Sigma = \{\alpha _i, \beta _j, \gamma _j\}$
of
$\Sigma = \{\alpha _i, \beta _j, \gamma _j\}$
of
![]() $CF(L_1,L_2)$
satisfying
$CF(L_1,L_2)$
satisfying
-
1.
 $\partial \alpha _i = 0$
,
$\partial \alpha _i = 0$
, -
2.
 $\partial \gamma _j = \beta _j$
, and
$\partial \gamma _j = \beta _j$
, and -
3.
 $\mathcal {A}(\gamma _1) - \mathcal {A}(\beta _1) \leq \mathcal {A}(\gamma _2) - \mathcal {A}(\beta _2) \leq \dots $
.
$\mathcal {A}(\gamma _1) - \mathcal {A}(\beta _1) \leq \mathcal {A}(\gamma _2) - \mathcal {A}(\beta _2) \leq \dots $
.
By using the above, we define the followings.
Definition 7.1.
-
1. A bar of
 $CF(L_1,L_2)$
is either
$CF(L_1,L_2)$
is either
 $\alpha _i$
or a pair
$\alpha _i$
or a pair
 $(\beta _j, \gamma _j)$
.
$(\beta _j, \gamma _j)$
. -
2. The length of a bar b is given by
 $$ \begin{align*} \text{the length of } b = \begin{cases} \infty & \text{if } b = \alpha_i, \\ \mathcal{A}(\gamma_j) - \mathcal{A}(\beta_j) & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \text{the length of } b = \begin{cases} \infty & \text{if } b = \alpha_i, \\ \mathcal{A}(\gamma_j) - \mathcal{A}(\beta_j) & \text{otherwise}. \end{cases} \end{align*} $$
-
3. Let
 $b_\epsilon (L_1,L_2)$
be the number of bars of
$b_\epsilon (L_1,L_2)$
be the number of bars of
 $CF(L_1,L_2)$
whose lengths are greater than or equal to
$CF(L_1,L_2)$
whose lengths are greater than or equal to
 $\epsilon $
.
$\epsilon $
.
Remark 7.2. We note that
![]() $\mathcal {A}$
is unique up to constant. More precisely, for an exact Lagrangian
$\mathcal {A}$
is unique up to constant. More precisely, for an exact Lagrangian
![]() $L_i$
, a choice of primitive function
$L_i$
, a choice of primitive function
![]() $h_i: L_i \to \mathbb {R}$
is not unique, but unique up to constant. Thus, it is easy to show that the length of bars depends only on
$h_i: L_i \to \mathbb {R}$
is not unique, but unique up to constant. Thus, it is easy to show that the length of bars depends only on
![]() $L_i$
and independent of the choice of primitive function
$L_i$
and independent of the choice of primitive function
![]() $h_i: L_i \to \mathbb {R}$
.
$h_i: L_i \to \mathbb {R}$
.
By Definition 7.1, Lemma 7.3 is obvious.
Lemma 7.3. Let
![]() $L_1$
and
$L_1$
and
![]() $L_2$
be a transversal pair of Lagrangians. Then, for any
$L_2$
be a transversal pair of Lagrangians. Then, for any
![]() $\epsilon \geq 0$
,
$\epsilon \geq 0$
,
It is well-known that
![]() $b_\epsilon $
is insensitive to small perturbations of the Lagrangians with respect to the Hofer distance. More precisely, Lemma 7.4 holds.
$b_\epsilon $
is insensitive to small perturbations of the Lagrangians with respect to the Hofer distance. More precisely, Lemma 7.4 holds.
Lemma 7.4. Let
![]() $L_1'$
be a Lagrangian satisfying
$L_1'$
be a Lagrangian satisfying
-
•
 $L_1'$
and
$L_1'$
and
 $L_1$
are Hamiltonian isotopic to each other,
$L_1$
are Hamiltonian isotopic to each other, -
•
 $d_H(L_1, L_1') < \frac {\delta }{2}$
with
$d_H(L_1, L_1') < \frac {\delta }{2}$
with
 $\delta < \epsilon $
, and
$\delta < \epsilon $
, and -
•
 $L_1'$
and
$L_1'$
and
 $L_2$
are transversal to each other.
$L_2$
are transversal to each other.
Then,
Proof. See [Reference Cineli, Ginzburg and Gürel13, Equations (3,13) and (3,14)]. We also refer the reader to [Reference Kislev and Shelukhin36], [Reference Polterovich, Rosen, Samvelyan and Zhang42], [Reference Usher and Zhang48].
Now, we extend the barcode counting function
![]() $b_\epsilon (L_1,L_2)$
to a good pair
$b_\epsilon (L_1,L_2)$
to a good pair
![]() $(L_1,L_2)$
defined in Definition 3.1. For a good pair, we set
$(L_1,L_2)$
defined in Definition 3.1. For a good pair, we set
where the limit is taken over Lagrangians
![]() $L_2'$
such that
$L_2'$
such that
![]() $L_2' \pitchfork L_1$
. We also note that
$L_2' \pitchfork L_1$
. We also note that
![]() $L_2$
and
$L_2$
and
![]() $L_2'$
should be Hamiltonian isotopic so that the Hofer distance between them is defined.
$L_2'$
should be Hamiltonian isotopic so that the Hofer distance between them is defined.
7.2 Barcode entropy
In the rest of this paper, we consider the same situation as what we considered in Section 4. For the reader’s convenience, we review the setting.
Let
![]() $(\hat {W}, d\lambda )$
be a Weinstein manifold and let
$(\hat {W}, d\lambda )$
be a Weinstein manifold and let
![]() $\phi : \hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism. Then, there is a Weinstein domain W such that
$\phi : \hat {W} \to \hat {W}$
be a compactly supported exact symplectic automorphism. Then, there is a Weinstein domain W such that
-
•
 $\hat {W} = W \cup \left ( [1,\infty ) \times \partial W\right )$
,
$\hat {W} = W \cup \left ( [1,\infty ) \times \partial W\right )$
, -
•
 $\lambda |_{[1,\infty \times \partial W)} = r \alpha $
where r is a coordinate for
$\lambda |_{[1,\infty \times \partial W)} = r \alpha $
where r is a coordinate for
 $[1.\infty )$
and
$[1.\infty )$
and
 $\alpha := \lambda |_{\partial W}$
, and
$\alpha := \lambda |_{\partial W}$
, and -
• the support of
 $\phi $
is contained in
$\phi $
is contained in
 $\mathrm {Int}(W)$
.
$\mathrm {Int}(W)$
.
Let
![]() $(L_1,L_2)$
be a good pair of Lagrangians with respect to W, that is,
$(L_1,L_2)$
be a good pair of Lagrangians with respect to W, that is,
Since
![]() $\phi $
is the identity outside of W,
$\phi $
is the identity outside of W,
![]() $\left (L_1,\phi ^n(L_2)\right )$
is also a good pair for any
$\left (L_1,\phi ^n(L_2)\right )$
is also a good pair for any
![]() $n \in \mathbb {Z}$
. Then, for a fixed
$n \in \mathbb {Z}$
. Then, for a fixed
![]() $\epsilon $
,
$\epsilon $
,
![]() $b_\epsilon \left (L_1, \phi ^n(L_2)\right )$
is well-defined. We would like to define the barcode entropy of
$b_\epsilon \left (L_1, \phi ^n(L_2)\right )$
is well-defined. We would like to define the barcode entropy of
![]() $\phi $
as the exponential growth rate of
$\phi $
as the exponential growth rate of
![]() $b_\epsilon \left (L_1, \phi ^n(L_2)\right )$
as
$b_\epsilon \left (L_1, \phi ^n(L_2)\right )$
as
![]() $n \to \infty $
.
$n \to \infty $
.
To be more precise, let
![]() $\log ^+: \mathbb {Z}_{\geq 0} \to \mathbb {R}$
be the function defined as
$\log ^+: \mathbb {Z}_{\geq 0} \to \mathbb {R}$
be the function defined as
 $$\begin{align*}\log^+(k) = \begin{cases} 0 \text{ if } k =0, \\ \log(k) \text{ other wise, } \end{cases}\end{align*}$$
$$\begin{align*}\log^+(k) = \begin{cases} 0 \text{ if } k =0, \\ \log(k) \text{ other wise, } \end{cases}\end{align*}$$
where the logarithm is taken base
![]() $2$
.
$2$
.
Definition 7.5.
-
1. For any
 $\epsilon \in \mathbb {R}_{\geq 0}$
, the
$\epsilon \in \mathbb {R}_{\geq 0}$
, the
 $\epsilon $
-barcode entropy of
$\epsilon $
-barcode entropy of
 $\phi $
relative to
$\phi $
relative to
 $(L_1,L_2)$
is
$(L_1,L_2)$
is  $$\begin{align*}h_\epsilon(\phi;L_1,L_2) := \lim_{n \to \infty} \frac{1}{n} \log^+ b_\epsilon\left(L_1, \phi^n(L_2)\right).\end{align*}$$
$$\begin{align*}h_\epsilon(\phi;L_1,L_2) := \lim_{n \to \infty} \frac{1}{n} \log^+ b_\epsilon\left(L_1, \phi^n(L_2)\right).\end{align*}$$
-
2. The barcode entropy of
 $\phi $
relative to
$\phi $
relative to
 $(L_1,L_2)$
is
$(L_1,L_2)$
is  $$\begin{align*}h_{bar}(\phi;L_1,L_2) := \lim_{\epsilon \searrow 0} h_\epsilon(\phi;L_1,L_2).\end{align*}$$
$$\begin{align*}h_{bar}(\phi;L_1,L_2) := \lim_{\epsilon \searrow 0} h_\epsilon(\phi;L_1,L_2).\end{align*}$$
We note that Definition 7.5 is the same as the notion of relative barcode entropy in [Reference Cineli, Ginzburg and Gürel13], except a minor adjustment to our set up.
7.3 Barcode vs topological entropy
In this subsection, we prove that for any good pair
![]() $(L_1, L_2)$
, the barcode entropy of
$(L_1, L_2)$
, the barcode entropy of
![]() $\phi $
bounds the topological entropy of
$\phi $
bounds the topological entropy of
![]() $\phi $
from below. The proof of Proposition 7.6 is almost same as the [Reference Cineli, Ginzburg and Gürel13, Proof of Theorem A].
$\phi $
from below. The proof of Proposition 7.6 is almost same as the [Reference Cineli, Ginzburg and Gürel13, Proof of Theorem A].
Proposition 7.6 (= The second inequality in Proposition 1.4).
For any good pair
![]() $(L_1,L_2)$
,
$(L_1,L_2)$
,
Proof. If
![]() $h_{bar}(\phi ;L_1,L_2) =0$
, then there is nothing to prove. Thus, let assume that
$h_{bar}(\phi ;L_1,L_2) =0$
, then there is nothing to prove. Thus, let assume that
![]() $h_{bar}(\phi ;L_1,L_2)>0$
. We would like to show that if
$h_{bar}(\phi ;L_1,L_2)>0$
. We would like to show that if
![]() $\alpha \leq h_{bar}(\phi ;L_1,L_2)$
, then
$\alpha \leq h_{bar}(\phi ;L_1,L_2)$
, then
![]() $\alpha \leq h_{top}(\phi )$
.
$\alpha \leq h_{top}(\phi )$
.
Let
![]() $\delta $
be a positive number. Since
$\delta $
be a positive number. Since
there is
![]() $\epsilon _0>0$
such that if
$\epsilon _0>0$
such that if
![]() $\epsilon < \epsilon _0$
, then
$\epsilon < \epsilon _0$
, then
![]() $h_\epsilon (\phi ;L_1,L_2)> \alpha -\delta $
. We fix a positive number
$h_\epsilon (\phi ;L_1,L_2)> \alpha -\delta $
. We fix a positive number
![]() $\epsilon $
such that
$\epsilon $
such that
![]() $2\epsilon < \epsilon _0$
.
$2\epsilon < \epsilon _0$
.
Since
there is an increasing sequence of natural numbers
![]() $\{n_i\}_{i \in \mathbb {N}}$
such that
$\{n_i\}_{i \in \mathbb {N}}$
such that
Now, we apply Lemma 3.2 to the good pair
![]() $\left (L_1, \phi ^{n_i}(L_2)\right )$
. Then, one obtains a family of Lagrangians
$\left (L_1, \phi ^{n_i}(L_2)\right )$
. Then, one obtains a family of Lagrangians
![]() $\{L^s\}_{s \in B^d_{\epsilon , n_i}}$
such that
$\{L^s\}_{s \in B^d_{\epsilon , n_i}}$
such that
-
(i)
 $L_1$
and
$L_1$
and
 $L^s$
are Hamiltonian isotopic for all
$L^s$
are Hamiltonian isotopic for all
 $s \in B^d_{\epsilon , n_i}$
,
$s \in B^d_{\epsilon , n_i}$
, -
(ii)
 $d_H(L_1,L^s) < \frac {\epsilon }{2}$
for all
$d_H(L_1,L^s) < \frac {\epsilon }{2}$
for all
 $s \in B^d_{\epsilon , n_i}$
, and
$s \in B^d_{\epsilon , n_i}$
, and -
(iii)
 $L^s \pitchfork \phi ^{n_i}(L_2)$
for almost all
$L^s \pitchfork \phi ^{n_i}(L_2)$
for almost all
 $s \in B^d_{\epsilon , n_i}$
.
$s \in B^d_{\epsilon , n_i}$
.
We point out that by the argument in the proof of Theorem 4.1, we can choose a family satisfying (i)–(iii) for all
![]() $n_i$
. Let
$n_i$
. Let
![]() $\{L^s\}_{s \in B^d_\epsilon }$
denote a fixed Lagrangian tomograph.
$\{L^s\}_{s \in B^d_\epsilon }$
denote a fixed Lagrangian tomograph.
Let
Then, one has
 $$\begin{align*}\int_{B^d_\epsilon} N_i(s) ds \leq C \cdot \mathrm{Vol}(\phi^{n_i}(L_2) \cap W),\end{align*}$$
$$\begin{align*}\int_{B^d_\epsilon} N_i(s) ds \leq C \cdot \mathrm{Vol}(\phi^{n_i}(L_2) \cap W),\end{align*}$$
by applying Lemma 3.4. We note that C is a constant independent from
![]() $n_i$
.
$n_i$
.
From Lemmas 7.3 and 7.4 and Equation (7.1), we have
Then, by taking integration over
![]() $B^d_{\epsilon }$
, one has
$B^d_{\epsilon }$
, one has
Since
![]() $\mathrm {Vol}(B^d_\epsilon )$
and C do not depend on
$\mathrm {Vol}(B^d_\epsilon )$
and C do not depend on
![]() $n_i$
,
$n_i$
,
 $$ \begin{align} \alpha - \delta \leq \limsup_{i\to \infty} \frac{1}{n_i} \log^+ \mathrm{Vol}\left(\phi^{n_i}(L_2) \cap W \right) \leq h_{top}(\phi|_W). \end{align} $$
$$ \begin{align} \alpha - \delta \leq \limsup_{i\to \infty} \frac{1}{n_i} \log^+ \mathrm{Vol}\left(\phi^{n_i}(L_2) \cap W \right) \leq h_{top}(\phi|_W). \end{align} $$
The last inequality holds due to Theorem 2.5, and because of the fact that
Finally, we note that
![]() $\phi $
is compactly supported, and that
$\phi $
is compactly supported, and that
![]() $\mathrm {supp}(\phi ) \subset W$
. Thus,
$\mathrm {supp}(\phi ) \subset W$
. Thus,
Thus, one has
This completes the proof.
7.4 Barcode vs categorical entropy
In the previous section, for an arbitrary good pair
![]() $(L_1,L_2)$
, we compared the barcode entropy of a triple
$(L_1,L_2)$
, we compared the barcode entropy of a triple
![]() $(\phi ;L_1,L_2)$
and the topological entropy of
$(\phi ;L_1,L_2)$
and the topological entropy of
![]() $\phi $
. As the result, we proved Proposition 7.6. In this subsection, we compare barcode and categorical entropy. However, in order to compare them, we should choose some specific pairs of Lagrangians.
$\phi $
. As the result, we proved Proposition 7.6. In this subsection, we compare barcode and categorical entropy. However, in order to compare them, we should choose some specific pairs of Lagrangians.
First, we choose a stop
![]() $\Lambda $
giving a fully stopped partially wrapped Fukaya category
$\Lambda $
giving a fully stopped partially wrapped Fukaya category
![]() $\mathcal {W}(W, \Lambda )$
. Let G be an embedded Lagrangian generating
$\mathcal {W}(W, \Lambda )$
. Let G be an embedded Lagrangian generating
![]() $\mathcal {W}(W,\Lambda )$
. As we did in the proof of Theorem 4.1, let
$\mathcal {W}(W,\Lambda )$
. As we did in the proof of Theorem 4.1, let
![]() $\varphi _0$
be a Hamiltonian isotopy satisfying
$\varphi _0$
be a Hamiltonian isotopy satisfying
-
(A)
 $\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
$\left (\varphi _0(G),\phi ^n(G)\right )$
is a good pair for all
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
, -
(B)
 $HW_\Lambda \left (G,\phi ^n(G)\right ) = HF\left (\varphi _0(G),\phi ^n(G)\right )$
for all
$HW_\Lambda \left (G,\phi ^n(G)\right ) = HF\left (\varphi _0(G),\phi ^n(G)\right )$
for all
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
As we showed before, one has
Since
![]() $\dim HF\left (\varphi _0(G),\phi ^n(G)\right )$
equals the number of bars having infinite length, one has
$\dim HF\left (\varphi _0(G),\phi ^n(G)\right )$
equals the number of bars having infinite length, one has
This induces Proposition 7.7.
Proposition 7.7 (= The first inequality in Proposition 1.4).
For G and
![]() $\varphi _0$
given above,
$\varphi _0$
given above,
Remark 7.8. We note that there always exists a good pair
![]() $(L_1,L_2)$
such that
$(L_1,L_2)$
such that
![]() $h_{bar}(\phi ;L_1,L_2)=0$
. By choosing a Lagrangian
$h_{bar}(\phi ;L_1,L_2)=0$
. By choosing a Lagrangian
![]() $L_2$
such that
$L_2$
such that
![]() $L_2$
does not intersect the support of
$L_2$
does not intersect the support of
![]() $\phi $
, one obtains a such pair. Thus, the choice of G (and
$\phi $
, one obtains a such pair. Thus, the choice of G (and
![]() $\varphi _0$
) in Proposition 7.7 is essential.
$\varphi _0$
) in Proposition 7.7 is essential.
7.5 Further questions
In this subsection, we discuss the questions given in Section 1.3 in more detail.
We also recall that
for any compact submanifold Y by [Reference Newhouse40], [Reference Przytycki43]. And it is known by [Reference Yomdin50] that
As one can see in the proof of Proposition 7.6,
![]() $h_{bar}(\phi ;L_1, L_2)$
bounds the exponential volume growth rate of
$h_{bar}(\phi ;L_1, L_2)$
bounds the exponential volume growth rate of
![]() $\phi ^n(L_2)$
from below. Thus,
$\phi ^n(L_2)$
from below. Thus,
As a generalization of Equation (7.3), one can ask whether the following equality holds or not:
The supremum in the above equation runs over the set of all good pairs. As mentioned in Remark 7.8, it is easy to find a good pair
![]() $(L_1,L_2)$
such that
$(L_1,L_2)$
such that
![]() $h_{bar}(\phi ;L_1,L_2)=0$
. Thus, we would like to remove such good pairs from the set where the supremum runs over, for computational convenience.
$h_{bar}(\phi ;L_1,L_2)=0$
. Thus, we would like to remove such good pairs from the set where the supremum runs over, for computational convenience.
Finally, we ask whether the following equality holds or not:
where G is a generating Lagrangian and
![]() $\varphi _0$
is a Hamiltonian isotopy satisfying the conditions in Section 7.4.
$\varphi _0$
is a Hamiltonian isotopy satisfying the conditions in Section 7.4.
On the other hand, one can ask a similar question for
![]() $h_{cat}(\phi )$
. More precisely, we ask whether the following equality holds or not:
$h_{cat}(\phi )$
. More precisely, we ask whether the following equality holds or not:
Acknowledgements
In Sections 3 and 7, and the proof of Theorem 4.1, we use the idea given in [Reference Cineli, Ginzburg and Gürel13] heavily. Also, Definition 7.5 is originally introduced in [Reference Cineli, Ginzburg and Gürel13]. The second named author appreciates Viktor Ginzburg for explaining the key ideas of [Reference Cineli, Ginzburg and Gürel13] in a seminar talk and a personal conversation. The first named author is grateful to Otto van Koert for helpful comments. The authors sincerely extend their heartfelt gratitude to the anonymous referee.
Funding
Hanwool Bae was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No.2020R1A5A1016126), and Sangjin Lee was supported by the Institute for Basic Science (IBS-R003-D1).