Published online by Cambridge University Press: 10 February 2011
The advent of frequency response analysers and the formulation of the universality of dielectric responses have between them greatly enhanced the usefulness of dielectric measurements as a diagnostic tool. The available frequency range was extended to between eight and twelve decades, making it possible to determine spectra with some precision. In addition, we now have a much more complete understanding than was available previously of the significance of various spectral shapes. For charge carrier systems the universal approach is based on the fractional power law of frequency dependence of the real and imaginary components of the susceptibility 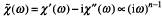 , where the exponent falls in the range O < n < 1. Values of n close to unity correspond to low-loss behaviour, values close to zero to very lossy processes dominated by low-frequency dispersion (LFD). Examples will be presented of both extremes and an indication will be given of the theoretical significance of these results. A brief discussion will be given of the physical principles of low-loss dielectrics showing “flat” or frequency-independent χ and of the opposite limit of LFD. It will be shown how the presence of universality simplifies the analysis of data and their interpretation.
, where the exponent falls in the range O < n < 1. Values of n close to unity correspond to low-loss behaviour, values close to zero to very lossy processes dominated by low-frequency dispersion (LFD). Examples will be presented of both extremes and an indication will be given of the theoretical significance of these results. A brief discussion will be given of the physical principles of low-loss dielectrics showing “flat” or frequency-independent χ and of the opposite limit of LFD. It will be shown how the presence of universality simplifies the analysis of data and their interpretation.