Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:17:37.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-Two-Dimensional Smectic States of DNA Molecules Intercalated between Lipid Membranes in Multi-Lamellar Phases

Published online by Cambridge University Press:  15 February 2011

Leonardo Golubović ,
Dorel Moldovan  and
Mirjana Golubović
Leonardo Golubović
Affiliation:
Physics Department, West Virginia University, Morgantown, WV 26506
Dorel Moldovan
Affiliation:
Physics Department, West Virginia University, Morgantown, WV 26506
Mirjana Golubović
Affiliation:
Physics Department, West Virginia University, Morgantown, WV 26506
Get access

Abstract

We study fluctuations of DNA-cationic lipid complexes in their lamellar membrane phases with DNA intercalated between lipid membranes. We theoretically elucidate this novel state of matter by characterizing it as the very first realization of a decoupled (unregistered) phase of strongly fluctuating 2-d smectic manifolds weakly interacting across membranes. Due to couplings between adjacent 2-d smectic Lx, × Ly planes, the experimentally observed ordinary 2-d smectic behavior [Salditt et al., Phys. Rev. Lett. 79, 2582 (1997)] of DNA in-plane undulations, with 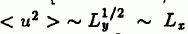, must cross over, at the longest scales, to a novel fluctuation behavior, with < u2 > ˜ (logLy )2 ˜ (logLx.)2.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 489: Symposium K – Materials Science of the Cell , 1997 , 13
Copyright
Copyright © Materials Research Society 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. See Gennes, P.G. de and Prost, J., The physics of liquid crystals (Claredon Press, Oxford, 1993).Google Scholar
2. Toner, J. and Nelson, D.R., Phys. Rev. B 23, 316 (1981).Google Scholar
3. Golubović, L. and Wang, Z.-G., Phys. Rev. Lett. 69, 2535 (1992), and Phys. Rev. E 49, 2567 (1994).Google Scholar
4. Radler, J., Koltover, I., Salditt, T., and Safinya, C.R., Science 275, 810 (1997).Google Scholar
5. Salditt, T., Koltover, I.. Radler, J., and Safinya, C.R., Phys. Rev. Lett. 79, 2582 (1997).Google Scholar
6. Unregistered states may occur also in lamellar phases of tethered membranes. See, Toner, J., Phys. Rev. Lett. 64, 1741 (1990); L. Golubović, Phys. Rev. Lett. 65, 1963 ( 1990); L. Golubović and T. C. Lubensky, Phys. Rev. A 43, 6793 (1991).Google Scholar
7. We note that the full nonlinear elastic energy functional of the decoupled phase must be invariant with respect to the local continuous translational invariance , , where f(z) is an arbitrary function of z [here we employed Lagrangian elasticity picture]. This reduces, for small strains, ∂ y u, ∂ y h « 1, to the harmonic approximation gauge invariance in Eq. (11). On the other side, in a columnar phase, the above continuous local symmetry is broken down to discrete local symmetry for which local translation f( z ) = l y m(z). Here m(z) is an arbitrary integer valued function of z =multiple of l x .Google Scholar
8. Sine-Gordon shear coupling (15) renormalizes (stiffens) the elastic constants K zx and K zy . To order A 2, this renormalization is of the form ΔK zx ˜ ∫ d 3 r x 2 K SG (r), with K SG (r) =< E SG (r) >E dec . By (11), we find K SG (r) δ(z) x −ω ˜ δδ(z) y −ω, with a nonuniversal exponent ω. E.g., for here η is the exponent entering Eq. (13). As ΔK zx must remain finite, it must be that ω > 4 (i.e., η > 2½/π) in the decoupled phase stability range. For ω > 4, arbitrarily weak Sine-Gordon shear coupling A is relevant and converts the decoupled phase into the columnar phase. From the above form of ω ˜ T, it is clear that the decoupled phase is only entropically favored over the columnar phase.E+dec+.+By+(11),+we+find+K+SG+(r)+δ(z)+x+−ω+˜+δδ(z)+y+−ω,+with+a+nonuniversal+exponent+ω.+E.g.,+for+here+η+is+the+exponent+entering+Eq.+(13).+As+ΔK+zx+must+remain+finite,+it+must+be+that+ω+>+4+(i.e.,+η+>+2½/π)+in+the+decoupled+phase+stability+range.+For+ω+>+4,+arbitrarily+weak+Sine-Gordon+shear+coupling+A+is+relevant+and+converts+the+decoupled+phase+into+the+columnar+phase.+From+the+above+form+of+ω+˜+T,+it+is+clear+that+the+decoupled+phase+is+only+entropically+favored+over+the+columnar+phase.>Google Scholar
9. Kamien, R.D. and Nelson, D.R., Phys. Rev. Lett. 74, 2499 (1995).Google Scholar