Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T01:33:57.323Z Has data issue: false hasContentIssue false
  • English
  • Français

A Model for the Distribution of Pore Sizes in Cement Paste

Published online by Cambridge University Press:  22 February 2011

D. Shi ,
P. W. Brown  and
S. Kurtz
D. Shi
Affiliation:
The Materials Research Laboratory, The Pennsylvania State University, University Park, PA 16802
P. W. Brown
Affiliation:
The Materials Research Laboratory, The Pennsylvania State University, University Park, PA 16802
S. Kurtz
Affiliation:
The Materials Research Laboratory, The Pennsylvania State University, University Park, PA 16802
Get access

Abstract

The pore size distribution in cement paste over the range of pore sizes interrogated by high pressure mercury intrusion porosimetry may be described by a mixture of two lognormal distributions. The compound distribution of pore sizes may be given as:

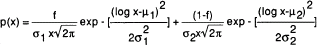
where p(x) is the probability density function of pores of size x, f and (1−f) are the weights of sub-distributions, μ1 and μ2 are the location parameters of sub-distributions, and σ1 and σ2 are the shape parameters of sub-distributions. These two sub-distributions may represent the larger and smaller capillary pores respectively. The changes in the sub-distributions and the compound distribution as functions of curing age and water-to-cement ratio are discussed.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 137: Symposium P – Pore Structure and Permeability of Cementitious Materials , 1988 , 23
Copyright
Copyright © Materials Research Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Diamond, S. and Dolch, W., J. Colloid & Interface Sci., 38, 234–244 (1972).Google Scholar
2. Fowlkes, E., J. Am. Stat. Assoc., 74, 561–575 (1979).Google Scholar
3. Aitchison, J. and Brown, J.A.C., The Lognormal Distribution, Cambridge Univ. Press, Cambridge (1957).Google Scholar
4. Tobias, P. and Trindade, D., Applied Reliability, Van Nostrand Reinhold Co., New York, 1986.Google Scholar
5. Irani, R., J. Phys. Chem., 63, 1603 (1959).Google Scholar
6. Irani, R. and Callas, A., Particle Size: Measurement, Interpretation. and Application, Wiley, New York (1963).Google Scholar
7. Hosmer, D., Communications in Stat., 1, 217–227 (1973).Google Scholar
8. Hasselblad, V., Technometrics, 8, 431–444 (1966).Google Scholar
9. Shi, D., M.S. Thesis, Purdue University (1984).Google Scholar
10. Kumar, A., Ph.D. Thesis, Penn. State University (1987).Google Scholar
11. Feldman, R., this Proceedings.Google Scholar
12. Gerhardt, R., this Proceedings.Google Scholar