Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-06T10:54:25.483Z Has data issue: false hasContentIssue false
  • English
  • Français

Grain-Boundary Slit Propagation in an Electric Field

Published online by Cambridge University Press:  15 February 2011

L. M. Klinger ,
X. Chuj ,
C. L. Bauer  and
W. W. Mullin
L. M. Klinger
Affiliation:
Department of Materials Engineering, The Technion, Haifa,Israel
X. Chuj
Affiliation:
t Department of Materials Science & Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania,USA
C. L. Bauer
Affiliation:
t Department of Materials Science & Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania,USA
W. W. Mullin
Affiliation:
t Department of Materials Science & Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania,USA
Get access

Abstract

Propagation (advancement) of a fine slit along a planar grain boundary in an electric field E0, applied parallel to the slit, is investigated by considering electromigration along both the grain boundary and the slit surface. Steady-state solutions of the transport equations are classified according to the value of a parameter β, which, under reasonable assumptions, depends on material constants only: for 5π/4 ≥ β > β2, unique steady-state solutions exist, for β2 > β > β1, multiple steady-state solutions exist, and for β1 ≥ β ≥ π/4, no steady-state solutions exist. For all steadystate solutions, slit width and tip velocity v scale as 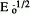and 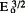, respectively. Generally, v can approach 1 nm/s (3.6 μm/h), thereby representing a likely failure mechanism in fine-line (near bamboo structure) interconnects.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 428: Symposium L – Materials Reliability in Microelectronics VI , 1996 , 155
Copyright
Copyright © Materials Research Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ho, P. S. and Kwok, T., Rep. Prog. Phys. 52, 301 (1989).Google Scholar
2. Rose, J. H., Appl. Phys. Lett. 61, 2170 (1992).Google Scholar
3. Arzt, E., Kraft, O., Nix, W. D. and Sanchez, J. E., J. Appl. Phys. 76, 1563 (1994).Google Scholar
4. Ramseyer, G. O., Beasock, J. V., Renz, T. E. and Walsh, L. H., Mater. Res. Soc. Symp. Proc. 338, 421 (1994).Google Scholar
5. Riege, S. P., Hunt, A. W. and Prybyla, J. A., Mat. Res. Soc. Symp. Proc. 391, 249 (1995).Google Scholar
6. Klinger, L. M., Chu, X., Bauer, C. L. and Mullins, W. W., submitted to J. Appl. Phys. (April 1996).Google Scholar
7. Chuang, T.-J. and Rice, J. R., Acta Met. 21, 1625 (1973).Google Scholar
8. Klinger, L. M., Glickman, E. E., Fradkov, V. E., Mullins, W. W. and Bauer, C. L., J. Appl.. Phys. 78, 1369 (1995).Google Scholar
9. Suo, Z., Wang, W., Yang, M., Appl. Phys. Lett. 64, 1944, (1994).Google Scholar