No CrossRef data available.
Article contents
Excitation of Coherent Phonons in Crystalline Bi: Theory for Driving Atomic Vibrations by Femtosecond Pulses
Published online by Cambridge University Press: 01 February 2011
Abstract
In this paper we show time-resolved experiment with 35 fs resolution on bismuth single crystal, for which very high sensitivity detection system has been used. Coherent and incoherent lattice dynamics as well as electrons dynamics can be clearly seen into the reflectivity changes. The complex behaviour of the reflectivity could not be explained in the light of the existing theories. Therefore, we developed a new theory, starting from the very basic principle of laser-matter interaction, which is in good agreement with experimental results. Two main results will be shown: the coherent phonon is excited by the temperature gradient; the changes in reflectivity are related directly to the changes in electron-phonon collision frequency.
- Type
- Research Article
- Information
- Copyright
- Copyright © Materials Research Society 2007


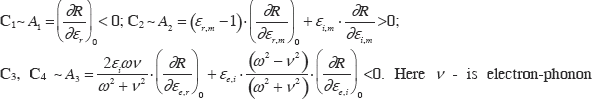 momentum exchange rate, ω is the laser frequency.
momentum exchange rate, ω is the laser frequency.