Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T07:31:36.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Constraints on Small Fullerene Helices

Published online by Cambridge University Press:  15 February 2011

Brett. I. Dunlap
Brett. I. Dunlap*
Affiliation:
Theoretical Chemistry Section, Code 6179, Naval Research Laboratory, Washington, DC 20375-3321
Get access

Abstract

A single heptagon together with a single pentagon can join two graphene semitubules together at a 30° angle so that all carbon atoms are three-fold coordinated and all other carbon rings are hexagons. This bend connects tubules of complementary classes. A tubule class is the set of all tubules having the same helicity. A tubule class has a uniform density of radii, which is the number of different tubules in the class per unit change in tubule radius. The classes that are joined by a heptagon and pentagon have smallest members whose radii differ by a factor of 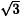. Thus tubule segments joined by a heptagon and pentagon cannot have exactly equal circumferences. There are only a finite number of twist angles allowed between sequential bends along a tubule. Pentagons and heptagons should be isolated and separated as far as possible. These requirements particularly constrain the bends and twists that can occur in the smallest tubules. These considerations favor long-range order along a helix, given a driving force for curling during the formation process.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 359: Symposium G – Science and Technology of Fullerene Materials , 1994 , 169
Copyright
Copyright © Materials Research Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Kroto, H.W., Heath, J.R., O'Brien, S.C., Curl, R.F. and Smalley, R.E.,Google Scholar
[2] Krätschmer, W., Lamb, L.D., Fostiropoulos, K., and Huffman, D.R., Nature 347, 354 (1990).Google Scholar
[3] Kroto, H.W., Nature 329, 529 (1987).Google Scholar
[4] Iijima, S., Nature (London) 354, 56 (1991).Google Scholar
[5] Dresselhaus, M.S., Dresselhaus, G., and Saito, R., Phys. Rev. B 45, 6234 (1992).Google Scholar
[6] Mintmire, J.W., Dunlap, B.I., and White, C.T., Phys. Rev. Lett. 68, 631 (1992).Google Scholar
[7] White, C.T., Robertson, D.H., and Mintmire, J.W., Phys. Rev. B 47, 5485 (1993).Google Scholar
[8] Dunlap, B.I., Phys. Rev. B 46, 1933 (1992).Google Scholar
[9] Iijima, S., Ajayan, P.M., and Ichihashi, T., Phys. Rev. Lett. 69, 3100 (1992).Google Scholar
[10] Dunlap, B.I., Phys. Rev. B 49, 5643 (1994).Google Scholar
[11] Dunlap, B.I., Phys. Rev. B 50, 8134 (1994).Google Scholar
[12] Zhang, X.B., Zhang, Z.F., Bernaerts, D., Tendeloo, G. Van, Amelinckx, S., Landruyt, J. Van, Ivanov, V., Nagy, J.B., Lambin, Ph., and Lucas, A.A., Europhys. Lett. 27, 141 (1994).Google Scholar
[13] Amelinckx, S., Zhang, X.B., Bernaerts, D., Zhang, X.F., Ivanov, V., Nagy, J.B., Science 265 635 (1994).Google Scholar
[14] Robertson, D.H., Brenner, D.W., and Mintmire, J.W., Phys. Rev. B 45, 12592 (1992).Google Scholar
[15] Fujita, M., Saito, R., Dresselhaus, G., and Dresselhaus, M.S., Phys. Rev. B, 45, 12834 (1992).Google Scholar