Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T07:27:16.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Atomic Transport by Ballistic Atomic Mixing Effect in Bilayer Structure

Published online by Cambridge University Press:  22 February 2011

K.H. Chae ,
J.M. Choi ,
S.M. Jung ,
J.H. Song ,
J.J. Woo  and
C.N. Whang
K.H. Chae
Affiliation:
Department of Physics, Yonsei University, Seoul 120-749, Republic of Korea
J.M. Choi
Affiliation:
Department of Physics, Yonsei University, Seoul 120-749, Republic of Korea
S.M. Jung
Affiliation:
Department of Physics, Yonsei University, Seoul 120-749, Republic of Korea
J.H. Song
Affiliation:
Department of Physics, Yonsei University, Seoul 120-749, Republic of Korea
J.J. Woo
Affiliation:
Department of Physics, Chonnam University, Kwangju 500-757, Republic of Korea
C.N. Whang
Affiliation:
Department of Physics, Yonsei University, Seoul 120-749, Republic of Korea
Get access

Abstract

A dynamic Monte-Carlo simulation (MCS) program, containing not only collisional mixing but also sputtering effects, has been used to elucidate the dynamic mixing processes and the atomic transport of constituents in Al-Pd bilayer systems. MCS results reveal that the preferential inward displacement of the top layer element dominates, and that there is an enhancement of the inward displacement when the heavier element is in the top layer. The inward displacement is controlled by both of an anisotropic and isotropic atomic transport. The anisotropic term is caused by the primary recoil of atoms, which has a characteristic of φ(ion dose) dependence, and the isotropic term is associated with the random cascade motion, which has a 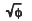dependence. However the outward displacement is governed by only the isotropic motion, thus the inward displacement always dominates over the outward motion, which leads to a preferential displacement of top layer element to the bottom layer.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 316: Symposium A – Materials Synthesis and Processing Using Ion Beams , 1993 , 277
Copyright
Copyright © Materials Research Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1 Liu, B. X., Phys. Stat. Sol. (a) 94, 11 (1986).Google Scholar
2 Sigmund, P. and Gras-Marti, A., Nucl. Instr. and Meth. 182/183, 25 (1981).Google Scholar
3 Van Rossum, M., Cheng, Y.-T., Nicolet, M.-A., and Johnson, W. L., Appl. Phys. Lett. 46, 610 (1985).Google Scholar
4 Sigmund, P., J. Appl. Phys. 50, 7261 (1979).Google Scholar
5 Kim, J. H., Kang, H. J., Chae, K. H., Song, J. H., Woo, J. J., and Whang, C. N., Nucl. Instr. and Meth. B7l, 271 (1992).Google Scholar
6 Ziegler, J. F., Biersack, J. P., and Littmark, U., The Stopping and Range of Ions in Solids (Pergamon Press, 1985) Vol. 1.Google Scholar
7 Brandt, W. and Kitagawa, M., Phys. Rev. B52, 5631 (1982).Google Scholar
8 Wang, Z. L., Nucl. Instr. and Meth. B2, 784 (1984).Google Scholar
9 Arfken, G., Mathmatical Methods For Physicists, 3rd ed. (Academic Press, 1985) pp. 566–569.Google Scholar
10 Chae, K. H., Choi, J. M., Jung, S. M., Joo, J. H. and Whang, C. N., to be published.Google Scholar
11 Banwell, T. and Nocolet, M. -A., J. Mater. Res. 3, 1072 (1988).Google Scholar
12 Cheng, Y. -T., Mater. Sci. Reports 5, 45 (1990).Google Scholar
13 Sigmund, P., Phys. Rev. 184, 383 (1969).Google Scholar
14 Sigmund, P., Nucl. Instr. and Meth. B34, 15 (1988).Google Scholar