Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T05:56:36.500Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation of Under- and Supersaturation of Gallium Vacancies in Gallium Arsenide During Silicon in- and Outdiffusion

Published online by Cambridge University Press:  10 February 2011

C.-H. Chen ,
U. Gösele  and
T. Y. Tan
C.-H. Chen
Affiliation:
Department of Mechanical Engineering and Material Science, Duke University, Durham, NC 27708–0300
U. Gösele
Affiliation:
Department of Mechanical Engineering and Material Science, Duke University, Durham, NC 27708–0300
T. Y. Tan
Affiliation:
Department of Mechanical Engineering and Material Science, Duke University, Durham, NC 27708–0300
Get access

Abstract

The diffusivity of Si in GaAs shows a dependence on the cubic power of its concentration or the concentration of electrons n under both in- and outdiffusion conditions. Hence, the diffusion of Si in GaAs is consistent with the Fermi-level effect model invoking the triply-negatively-charged Ga vacancies, 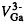, as the point defect species responsible for diffusion to occur on the Ga sublattice under n-doping condition. However, the Si diffusivity values of the indiffusion cases is several orders of magnitude smaller than those of the outdiffusion cases at the same Si concentrations. This means that the two apparent Si diffusivity values under intrinsic conditions will contain also the same discrepancy, which has been previously assessed to be due to a 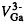undersaturation in indiffusion cases and a 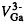supersaturation in outdiffusion cases. In this study we have calculated the 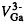under- and supersaturation values using the known Si diffusivities. We found that the GaAs surface states play a key role in the development of the 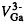under- and supersaturations.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 490: Symposium Q – Semiconductor Process & Device Performance Modeling , 1997 , 99
Copyright
Copyright © Materials Research Society 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1. Vieland, L. J., J. Phys. Chem. Solid 21, 318 (1961).Google Scholar
2. Anteil, G.R., Solid-State Electron. 8, 943 (1965).Google Scholar
3. Kavanagh, K. L., Magee, C. W., Sheets, J., and Mayer, J. W., J. Appl. Phys. 64, 1845 (1988).Google Scholar
4. Yu, S., Tan, T. Y. and Gösele, U. M., J. Appl. Phys. 66, 2952 (1989).Google Scholar
5. You, H. M., Gösele, U. M. and Tan, T. Y., J. Appl. Phys. 73, 7207 (1993).Google Scholar
6. Tan, T. Y. and Gösele, U. M., Appl. Phys. Lett. 52, 1240 (1988).Google Scholar
7. Tan, T. Y., You, H. M. and Gösele, U. M., Appl. Phys. A. 56, 249 (1993).Google Scholar
8. Jüngling, W., Pichler, P., Selberherr, S., Guerrero, E., and Pötzl, H. W., IEEE Trans. Electron. Devices ED-32, 156 (1985).Google Scholar