Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-06T08:31:25.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling Behavior Of Dynamic Permeability In Porous Media

Published online by Cambridge University Press:  22 February 2011

Ping Sheng ,
Min-Yao Zhou ,
E. Charlaix ,
A. Kushnick  and
J. P. Stokes
Min-Yao Zhou
Affiliation:
Exxon Research and Engineering Co., Route 22 East, Clinton Township Annandale, NJ 08801
Get access

Abstract

We show that the scaling of the dynamic permeability κ(ω) by its static value κ0 and the frequency ω by a characteristic frequency ω0 particular to the medium results in a dimensionless function 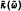, with 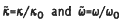, which is dominated by the geometry of the throat regions in a porous medium. If the pore cross sectional area S varies slowly near the throat, i.e. dS/dz ≃ 0 where z is the distance normal to the cross section, then 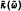is an approximate universal function independent of microstructures. When scaling holds, the dynamic permeability κ(ω) is shown to contain only two pieces of geometric information, and the knowledge of either the low-frequency or the high-frequency asymptotic constants of κ(ω) would enable one to deduce the other missing parameters. In particular, since the high-frequency asymptotic parameters of κ(ω) can be related to the electrical formation factor and the volume-to-surface ratio, the static permeability value κ0 may be directly deduced from such non-permeability measurements.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 137: Symposium P – Pore Structure and Permeability of Cementitious Materials , 1988 , 35
Copyright
Copyright © Materials Research Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References and Footnotes

1. Katz, A.J. and Thompson, A.H., Phys. Rev. B 34, 8179 (1986).CrossRefGoogle Scholar
2. Thompson, A.H., Katz, A.J., and Krohn, C.E., Adv. in Phys. 36, 625 (1987).CrossRefGoogle Scholar
3. Johnson, D.L., Koplik, J., and Schwartz, L.M., Phys. Rev. Lett. 57, 379 (1987).Google Scholar
4. Johnson, D.L., Koplik, J. and Dashen, R., J. Fluid Mech. 176, 379 (1987).CrossRefGoogle Scholar
5. Sheng, P. and Zhou, M.Y., Phys. Rev. Lett. 61, 1591 (1988).CrossRefGoogle Scholar
6. Charlaix, E., Kushnick, A., and Stokes, J.P., Phys. Rev. Lett. 61, 1595 (1988).CrossRefGoogle Scholar
7. Zhou, M.Y. and Sheng, P., to be published.Google Scholar
8. Burridge, R. and Keller, J.B., J. Acoust. Soc. Am. 70, 1140 (1981). Our treatment of the ε scaling differs from the reference above in that we treat ω as an external parameter, and all the scaling units are taken from intrinsic material constants of the medium.CrossRefGoogle Scholar
9. Biot, M.A., J. Acoust. Soc. Am. 34, 1254 (1962).CrossRefGoogle Scholar
10. Bedford, A., Costley, R.D., and Stern, M., J. Acoust. Soc. Am. 76, 1804 (1984).CrossRefGoogle Scholar
11. Brown, R.J.S., Geophysics 45, 1269 (1980).CrossRefGoogle Scholar
12. Ambegaokar, V., Halperin, B.I., and Langer, J.S., Phys. Rev. B 4, 2612 (1971).CrossRefGoogle Scholar
13. Sheng, P. and Klafter, J., Phys. Rev. B27, 2583 (1983); J. Klafter and P. Sheng, J. Phys. CL., L93 (1984).CrossRefGoogle Scholar